Решение задачи об использовании ресурсов симплексным методом.
Вариант №10.
Условие задачи:
На предприятии имеется сырье видов I, II и III. Из него можно изготовить изделия типов A и B. Запасы сырья на предприятии составляют S1, S2 и S3 единиц соответственно. Изделие типа A дает прибыль c1 у.е., изделие типа B - c2 у.е. Расход сырья на изготовление одного изделия задан в условных единицах таблицей.
| Изделие | Расход сырья на одно изделие | Запасы сырья | Прибыль | |||||
| I | II | III | S1 | S2 | S3 | c1 | c2 | |
| A | ||||||||
| B |
Составить план выпуска изделий, при котором предприятие имеет наибольшую прибыль. Решить задачу симплексным методом:
1. С помощью преобразования уравнений.
2. С помощью симплексных таблиц.
Решение задачи:
Решение с помощью преобразования уравнений.
Целевая функция:
 .
.
Ограничения:
 ,
,  ,
,  .
.
С помощью дополнительных неотрицательных переменных перейдем от системы неравенств к системе уравнений:

1. Найдем первое базисное решение:
Пусть  ,
,  ,
,  - базисные переменные, тогда
- базисные переменные, тогда  ,
,  - свободные. Выразим базисные переменные через свободные:
- свободные. Выразим базисные переменные через свободные:

Таким образом, первым базисным решением станет  при
при  ,
,  .
.
Найдем значение целевой функции, выраженной через свободные переменные:
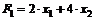 .
.
 .
.
Значение функции (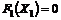 ) может возрасти за счет увеличения любой из свободных переменных, входящих в формулу с положительными коэффициентами, следовательно, полученное значение целевой функции не является максимальным, а базисное решение - оптимальным.
) может возрасти за счет увеличения любой из свободных переменных, входящих в формулу с положительными коэффициентами, следовательно, полученное значение целевой функции не является максимальным, а базисное решение - оптимальным.
2. Перейдем ко второму базисному решению:
Пусть переменная  станет новой базисной, в связи с тем, что она имеет наибольший положительный коэффициент в целевой функции
станет новой базисной, в связи с тем, что она имеет наибольший положительный коэффициент в целевой функции  . Так как все переменные должны быть неотрицательными, то решим систему неравенств и определим новую свободную переменную:
. Так как все переменные должны быть неотрицательными, то решим систему неравенств и определим новую свободную переменную:


Таким образом, наибольшее возможное значение переменной  , которая станет новой базисной, равно
, которая станет новой базисной, равно  и достигается во втором уравнении системы, следовательно, переменная
и достигается во втором уравнении системы, следовательно, переменная  станет новой свободной. Уравнение, в котором достигается наибольшее возможное значение переменной, переводимой в базисные, называется разрешающим.
станет новой свободной. Уравнение, в котором достигается наибольшее возможное значение переменной, переводимой в базисные, называется разрешающим.
3. Найдем второе базисное решение:
Пусть  ,
,  ,
,  - базисные переменные, тогда
- базисные переменные, тогда  ,
,  - свободные. Выразим новые базисные переменные через новые свободные, начиная с разрешающего уравнения:
- свободные. Выразим новые базисные переменные через новые свободные, начиная с разрешающего уравнения:


Таким образом, вторым базисным решением станет  при
при  ,
,  .
.
Выразим целевую функцию через свободные переменные и найдем ее значение:
 .
.
 .
.
Значение функции ( ) не может возрасти за счет увеличения свободных переменных, входящих в формулу с отрицательными коэффициентами, следовательно, полученное значение целевой функции является максимальным, а базисное решение - оптимальным.
) не может возрасти за счет увеличения свободных переменных, входящих в формулу с отрицательными коэффициентами, следовательно, полученное значение целевой функции является максимальным, а базисное решение - оптимальным.
Решение с помощью симплексных таблиц.
Введем дополнительные неотрицательные переменные в систему уравнений и целевую функцию:

1. Составим первую симплексную таблицу:
Таблица 1.
| Базисные переменные | 
| Переменные | ||||

| 
| 
| 
| 
| ||

| ||||||

| ||||||

| ||||||

| -2 | -4 |
Критерий оптимальности не выполнен, так как в последней строке присутствуют отрицательные коэффициенты. Наибольший по модулю отрицательный коэффициент в последней строке ( ) определяет разрешающий столбец (
) определяет разрешающий столбец ( ).
).
Определим оценочные отношения каждой строки первой симплексной таблицы, разделив элементы столбца  на соответствующие элементы разрешающего столбца (
на соответствующие элементы разрешающего столбца ( ):
):
Таблица 2.
| Базисные переменные | 
| Переменные | |||||

| 
| 
| 
| 
| Оценочное отношение | ||

| |||||||

| |||||||

| |||||||

| -2 | -4 |
Минимальное значение оценочного отношения ( ) определяет оценочную строку (
) определяет оценочную строку ( ). На пересечении разрешающего столбца и разрешающей строки находится разрешающий элемент
). На пересечении разрешающего столбца и разрешающей строки находится разрешающий элемент  .
.
2. Перейдем ко второй симплексной таблице по правилам:
- в столбце  запишем новый базис
запишем новый базис  (то есть перенесем значения столбца
(то есть перенесем значения столбца  в столбец
в столбец  );
);
- в столбцах, соответствующих базисным переменным, проставим нули и единицы (1 – против «своей» переменной, 0 – против «чужой», 0 – в последней строке базисных переменных);
- новую строку  получим из старой
получим из старой  путем деления ее значений на разрешающий элемент
путем деления ее значений на разрешающий элемент  ;
;
- остальные элементы вычислим по правилу прямоугольника.
Таблица 3.
| Базисные переменные | 
| Переменные | ||||

| 
| 
| 
| 
| ||

| -1 | |||||

| 1/2 | 1/2 | ||||

| 5/2 | -1/2 | ||||

|
Теперь критерий оптимальности выполнен, так как в последней строке отсутствуют отрицательные коэффициенты, значит 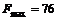 при оптимальном базисном решении
при оптимальном базисном решении 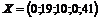 .
.