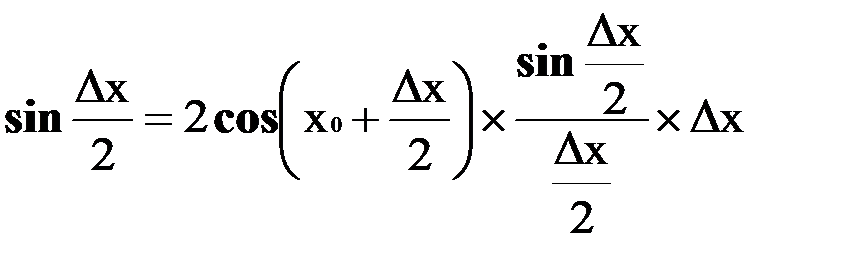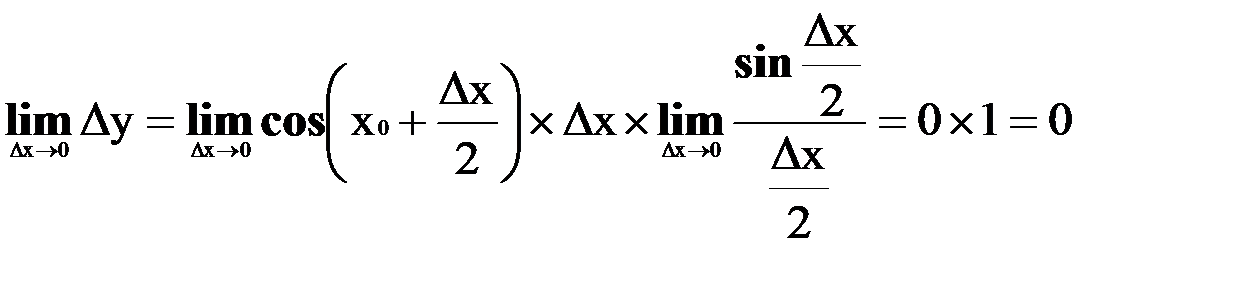12. Решение систем методом обратной матрицы.
Матрицей, обратной квадратной матрице А называется квадратная матрица 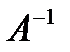 , удовлетворяющая равенствам:
, удовлетворяющая равенствам: 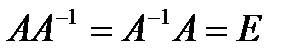 , где Е- единичная матрица
, где Е- единичная матрица
Рассмотрим квадратную матрицу порядка n:
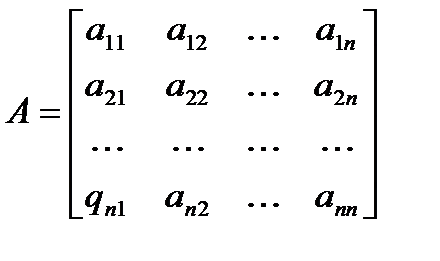 (*)
(*)
Опр. Матрицей, присоединенной к матрице А, называется матрица
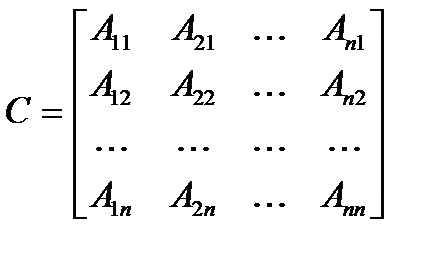 ,
,
где 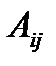 - алгебраическое дополнение элемента
- алгебраическое дополнение элемента 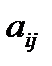 матрицы А, причем алгебраические дополнения элементов i -той строки матрицы А расположены в i -том столбце матрицы С.
матрицы А, причем алгебраические дополнения элементов i -той строки матрицы А расположены в i -том столбце матрицы С.
Опр. Квадратная матрица называется невырожденной, если ее определитель отличен от нуля.
Т. Всякая невырожденная квадратная матрица А (*) имеет единственную обратную матрицу
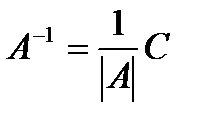 ,
,
где С- присоединенная матрица, |A| - определитель матрицы А.
Свойства:
1. 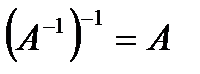
2. 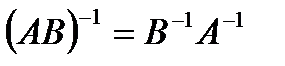
3. 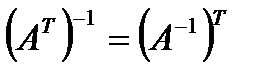
4.det 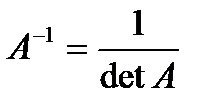
Построение обратной матрицы:
Надо сначала составить матрицу из алгебраических дополнений, транспонировать ее, получим присоединенную матрицу С. Затем каждый ее элемент надо разделить на определитель исходной матрицы.
Например:
Найти обратную для матрицы 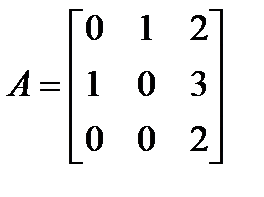
Решение:
1) 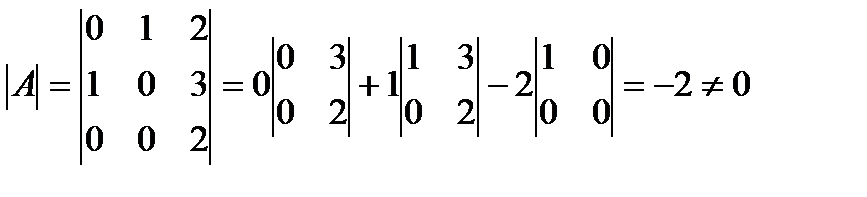
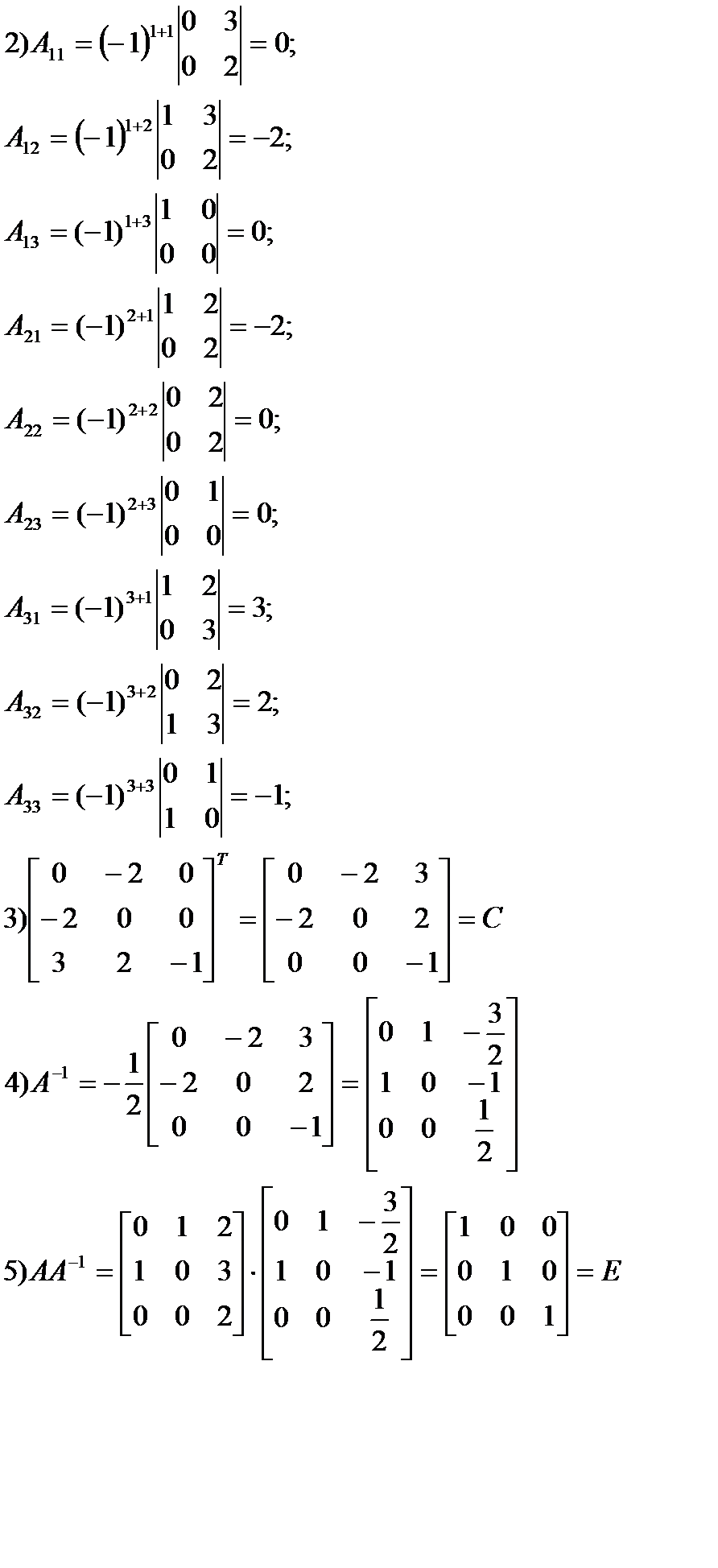
13. Понятие вектора на плоскости и в пространстве, линейные операции над векторами в геометрической форме.
Векторная величина характеризуется числом и направлением.
Сила (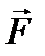 ) Ускорение (
) Ускорение (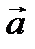 )
)
Для геометрического изображения векторных величин служат векторы.
Вектором называется направленный отрезок.
| C |
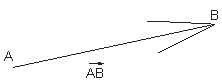
Длина вектора 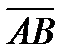 обозначается
обозначается 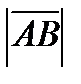 ,
, 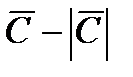 .
.
Единичным вектором называется вектор, длина которого равна единице.
Нулевой вектор – это вектор, начало, и конец которого совпадают.
Векторы, лежащие на параллельных прямых или на одной прямой называются коллинеарными.
Векторы лежащие на одной прямой или на параллельных прямых и имеющие одинаковое направление называются однонаправленными.
Векторы лежащие на одной прямой или на параллельных прямых и имеющие разное направление называются разнонаправленные.
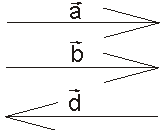

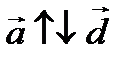


Два вектора называются равными если они коллинеарны, направлены в одну сторону и имеют равные длины.
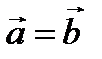
Векторы лежащие в параллельных плоскостях или в одной плоскости называются компланарными.
Пусть в пространстве задан вектор 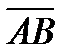 и ось
и ось 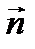 ;
;
А1= пр. 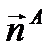 и В1= пр.
и В1= пр.  ;
; 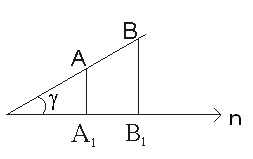
Проекцией вектора 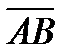 на ось
на ось 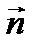 называется алгебраическая величина отрезка А1В1, то есть длина отрезка А1В1 со знакам «+» будет в том случае, если его направление совпадает с направлением оси. Знак «-», если его направление не совпадает с направлением оси.
называется алгебраическая величина отрезка А1В1, то есть длина отрезка А1В1 со знакам «+» будет в том случае, если его направление совпадает с направлением оси. Знак «-», если его направление не совпадает с направлением оси.
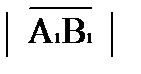 = пр.
= пр. 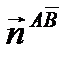
Если 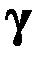 - угол между
- угол между 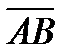 и осью
и осью 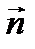 , то пр.
, то пр. 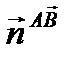 =
= 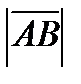 COS
COS 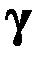 ;
;
Равные векторы имеют равные проекции на одну ось.
Рассмотрим в пространстве декартову прямоугольную систему координат, (три взаимно перпендикулярные упорядоченные оси OX, OY, OZ).
Радиус-вектором точки М называется вектор 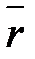 =
= 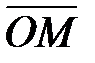 начало координат которого совпадает с началом координат, конец в точке М. Точки А, В, С – проекциями точки М на оси OX, OY, OZ.
начало координат которого совпадает с началом координат, конец в точке М. Точки А, В, С – проекциями точки М на оси OX, OY, OZ.
14. Прямоугольная декартовая система координат, координаты вектора. Длинна вектора, линейные операции над векторами в прямоугольной и декартовой системе координат.
Декартовыми прямоугольными координатами X, Y, Z вектора 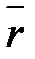 называются его проекции на координатные оси:
называются его проекции на координатные оси:
X - проекция на ось X вектора 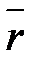 ;
;
Y - проекция на ось Y вектора 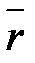 ;
;
Z - проекция на ось Z вектора 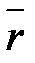 ;
;
Или 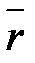 (X,Y,Z), то есть вектор
(X,Y,Z), то есть вектор 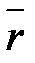 имеет координаты (X,Y,Z).
имеет координаты (X,Y,Z).
Z
Координаты радиус-вектора ОМ равны
координатам точки М(x,y,z). Базисом в
C пространстве называется упорядоченная
тройка некомпланарных векторов.
M
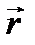
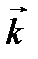
O Y
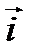
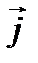 B
B
A
X
Введем в рассмотрение единичные векторы 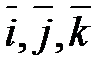 координатных осей (орты).
координатных осей (орты).
Вектор 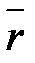 (X,Y,Z) можно разложить по базисным векторам
(X,Y,Z) можно разложить по базисным векторам 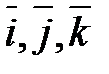 :
:
1) 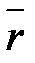 = X
= X  +Y
+Y 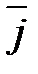 +Z
+Z 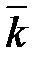 - составляющие вектора
- составляющие вектора 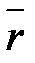 ;
;
2) 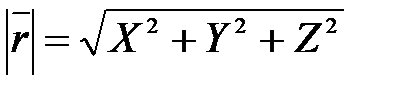 - длина вектора через его координаты.
- длина вектора через его координаты.
Если даны две точки М1(x1,y1,z1) и М2(x2,y2,z2) тогда координаты вектора находятся по формуле:
3) 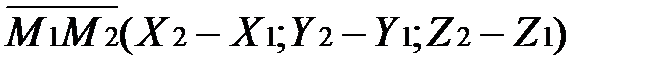
А его длина:
4) 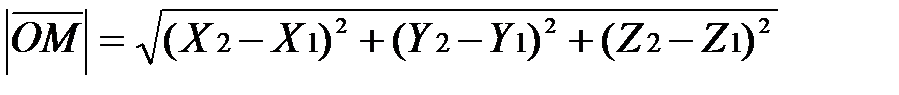 - так же определяет расстояние между двумя точками.
- так же определяет расстояние между двумя точками.
15. Скалярное произведение векторов: определение, свойства, вычисление в координатной форме.
Скалярным произведением двух векторов называется число равное произведению двух длин на косинус угла между ними:
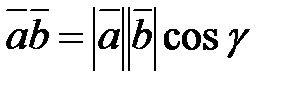 где
где 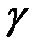 - угол между ними.
- угол между ними.
Физический смысл: если вектор 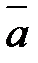 изображает силу, точка приложения которой перемещается из начала в конец вектора
изображает силу, точка приложения которой перемещается из начала в конец вектора 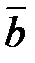 , то работа указанной силы определяется равенством:
, то работа указанной силы определяется равенством:
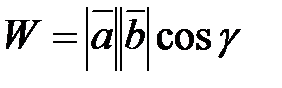 , т.е. скалярное произведение векторов
, т.е. скалярное произведение векторов 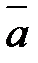 и
и 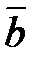 .
.
Свойства скалярного произведения:
1) 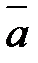
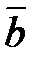 =
= 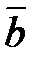
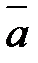 (переместительное свойство).
(переместительное свойство).
2) 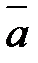 (
(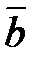 +
+ 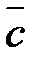 )=
)= 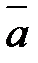
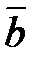 +
+ 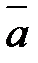
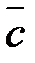 (распределительное свойство).
(распределительное свойство).
3) 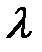 (
(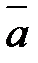
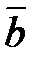 )=(
)=(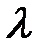
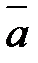 )
) 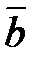 =
= 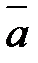 (
(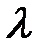
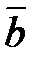 ) (сочетательное свойство).
) (сочетательное свойство).
Скалярное произведение 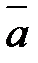
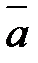 называется скалярным квадратом
называется скалярным квадратом 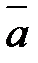 и обозначается
и обозначается 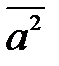 и равно квадрату его длины:
и равно квадрату его длины:
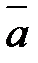
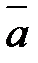 =
= 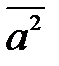 =
= 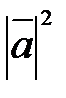 .
.
Если векторы 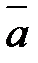 и
и 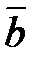 имеют соответствующие координаты (X1,Y1,Z1) и (X2,Y2,Z2), то их скалярное произведение с координатной форме выразится формулой:
имеют соответствующие координаты (X1,Y1,Z1) и (X2,Y2,Z2), то их скалярное произведение с координатной форме выразится формулой:
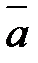
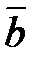 =X1X2+Y1Y2+Z1Z2.
=X1X2+Y1Y2+Z1Z2.
Угол между ними:
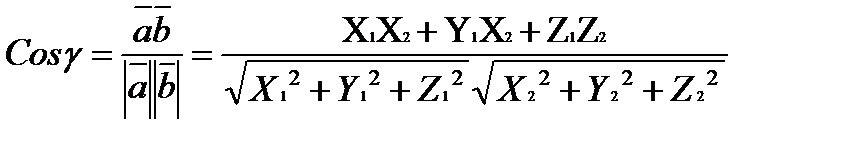
Тогда необходимое и достаточное условие перпендикулярности векторов 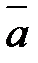 и
и 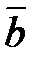 будет:
будет:
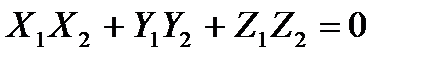
16. Векторное произведение векторов: определение, свойства, вычисление в координатной форме.
Определение. Векторным произведением двух векторов 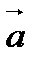 и
и 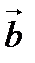 называют третий вектор
называют третий вектор 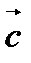 , удовлетворяющий условиям:
, удовлетворяющий условиям:
1) 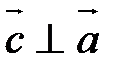 ,
, 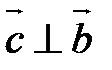
2) 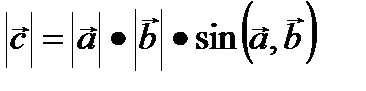
3) Реперы 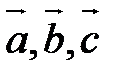 и
и 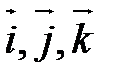 имеют одинаковую ориентацию.
имеют одинаковую ориентацию.
Обозначается: 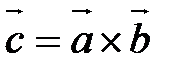
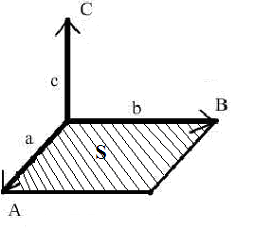
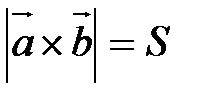 , где S – площадь параллелограмма, построенного на векторах
, где S – площадь параллелограмма, построенного на векторах 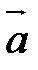 и
и 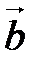 .
.
Если 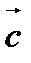 - единичный вектор направления
- единичный вектор направления 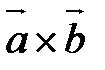 , то векторное произведение может быть выражено:
, то векторное произведение может быть выражено:
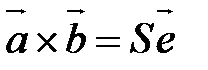
|
Векторное произведение ненулевых векторов равно нулю тогда и только тогда, когда вектора 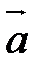 и
и 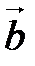 коллинеарны:
коллинеарны:
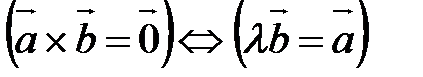 . В частности
. В частности 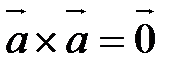
Свойства векторного произведения:
1) Антиперестановочность множителей: 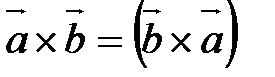
2) 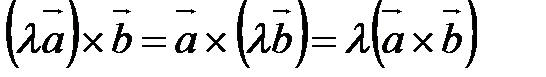 - сочетательность относительно скалярного множителя.
- сочетательность относительно скалярного множителя.
3) 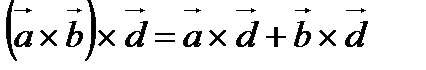 - распределительность относительно сложения.
- распределительность относительно сложения.
Теорема. Если вектора 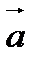 и
и 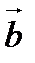 заданы своими координатами, т.е.
заданы своими координатами, т.е. 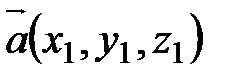 ,
, 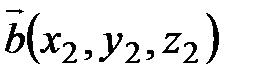 , то
, то 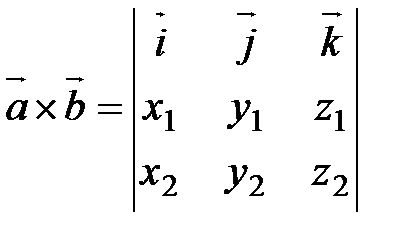
или 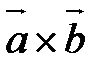 имеет координаты:
имеет координаты:
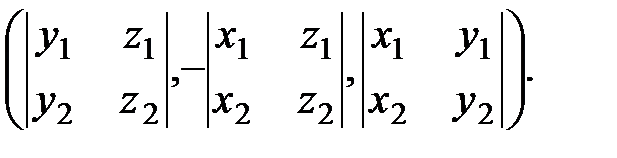
Пример:
1) Найти векторные произведения единичных векторов правой системы координат 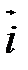 ,
, 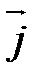 ,
, 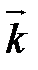 :
:
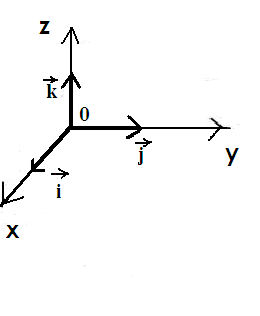
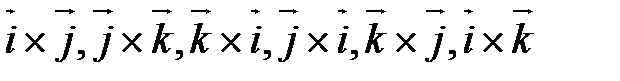
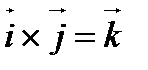 или или 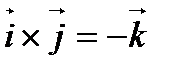 ; ;
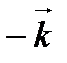 - «отбрасывается», т.к. репер - «отбрасывается», т.к. репер 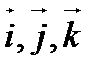 - левый. - левый.
|
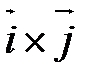 коллинеарен
коллинеарен 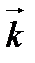

вектор 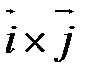 единичный
единичный
Аналогично: 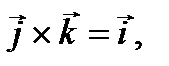
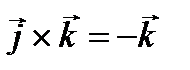 ,
,
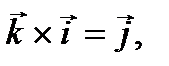
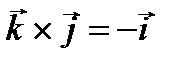 ,
,
 .
.
2) Даны вектора а(7;-5;-6), в(1;-2;-3), найти координаты 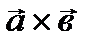 :
:
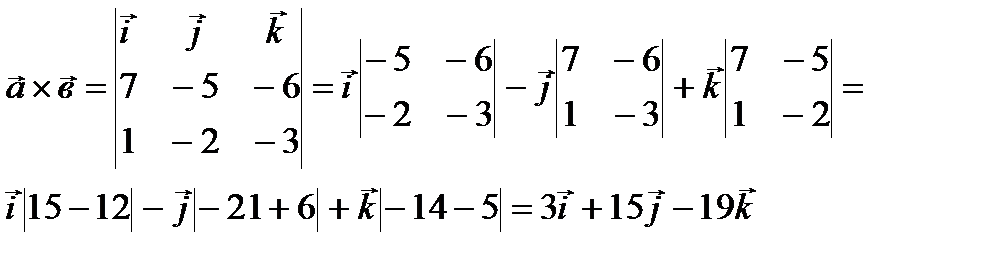
Ответ: (3;15;19)
17. Смешанное произведение векторов: определение, свойства, вычисление в координатной форме.
Ответ: Смешанным произведением 3-х векторов 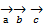 наз. число равное векторному произведению
наз. число равное векторному произведению 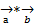 умноженному скалярного на вектор
умноженному скалярного на вектор
Смешанное произведение 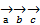 3-ёх некомпланарных векторов равно объему параллелепипеда построенного на веккторах
3-ёх некомпланарных векторов равно объему параллелепипеда построенного на веккторах 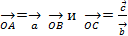 взятому со знаком +когда реперы
взятому со знаком +когда реперы 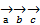 и
и 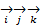 имеют одинаковую ориентацию и со знаком – в противном случаи.
имеют одинаковую ориентацию и со знаком – в противном случаи.
18. Понятие функции, ее свойства, график, способы задания.
Свойства
1)Четность и нечетность
2) Периодичность
3)Моннотонная
4)Ограниченность
Графиком функции - множество точки плоскости с координатами (x;f(x))
Если у? У ставится в соответствии единств х? Х такой что f(x)=y то получаем функцию х’= 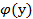 заданую на множестве У со значениями в Х обратную x y=f(x)
заданую на множестве У со значениями в Х обратную x y=f(x)
19. Элементарные функции. Графики основных элементарных функций.
Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций:
многочлен,
рациональная,
степенная,
показательная и логарифмическая,
тригонометрические и обратные тригонометрические.
Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения. Иногда к основным элементарным функциям относят также гиперболические и обратные гиперболические функции, хотя они могут быть выражены через перечисленные выше основные элементарные функции.
Элементарные функции разделяются на алгебраические и трансцендентные.
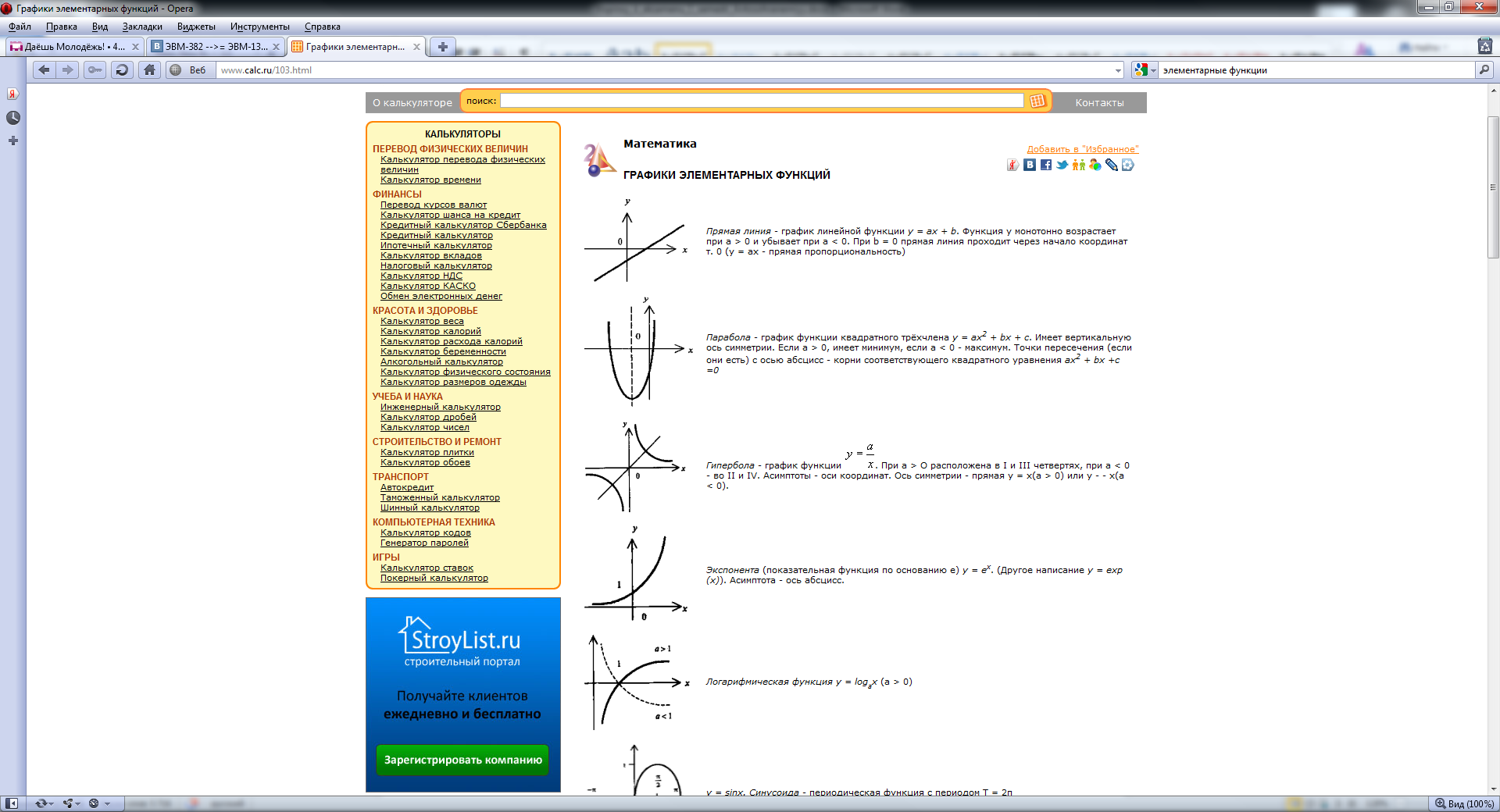 я думаю сто хватит если чё вот сслыка ссайта https://www.calc.ru/103.html
я думаю сто хватит если чё вот сслыка ссайта https://www.calc.ru/103.html
20. Обратная функция. Сложная функция Неявно заданная функция, параметрический заданная функция.
21. Различные виду уравнений прямой на плоскости. Взаимное расположение прямых, угол между прямыми, расстояние от точки до прямой.
Уравнение линии на плоскости наз. уравнение относительно переменных х и у которому удовлетворяет координаты любой точки данной линии. Уравнением линии на плоскости в декартовых прямоугольных координатах F(x,y)=0
Точки пересечением двух линий F1 (x,y), F2 (x,y)=0 находим из системы уравнений 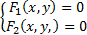 если системы не имеет решений то точек пересечений нет.
если системы не имеет решений то точек пересечений нет.
Виды уравнение прямой на плоскасти
1)y=kx +b-уравнение прямой с угловым коэфициэнтом где k- угловой коэфициэнт b-отрезок отсекаемыый ею на оси OY k=tg
2)Ax+By+C=0 общее уравнение прямой A и B одновременно нулю не обращаются 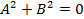
3) 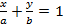 –уравнеение прямой в отрезках где a и b длины отрезков отсекаемых на осях координат взятые с соответствующим законом
–уравнеение прямой в отрезках где a и b длины отрезков отсекаемых на осях координат взятые с соответствующим законом
4) 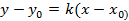 уравнение прямой с угловым коэфициэнтом K и проходяшим через данную точку
уравнение прямой с угловым коэфициэнтом K и проходяшим через данную точку 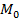 (
(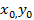 )
)
5) 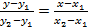 -уравнение прямой проходящее через две данные точки
-уравнение прямой проходящее через две данные точки 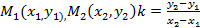
Растояние от точки прямой наз.длина пенпердикуляра опущеного из этой точки на данную прямую
22. Кривые 2-го порядка: канонические уравнения, основные характеристики, изображение кривых.
Кривыми второго порядка наз. линии уравнения которых могут быть записаны следующим образом
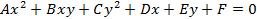
Где A,B,C,D,E,F –действительные числа которые наз. коэффициентами уравнениями при чем по крайне мере один из коэффициентов A,B,C отличен от 0.
Каноническое уравнение окружности 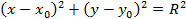
Если уравнение второй степени второй степени
Определяет не которую линию то это линия окружности а данное уравнение приводится к каноническому путем дополнение полных квадратов
Эллипс
Эллипсом –наз. Множество всех точек плоскости сумма расстояний от каждой до двух данных точек f1 и f2 (фокусы эллипса) есть величина постоянная
Уравнение Эллипса 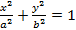
Гипербола
Каноническое уравнение 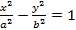
Парабола
Параболой наз. множество точек плоскости равно удалённых от данной точки (наз. фокусом) и данной прямой (наз. директрисой)
Уравнение 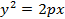
Основное характеристическое свойство параболы: все точки параболы равноудалены от директрисы и фокуса.Существуют иные формы канонического уравнения параболы, которые определяют другие направления ее ветвей в системе координат
23. Уравнение плоскости в пространстве. Взаимно расположенные плоскости. Угол между плоскостями. Расстояние от точки до плоскости.
F(x,y,z)=0 – уравнение поверхности в пространстве
Уравнение плоскости проходящей через данную точку m0(x0,y0,z0) Перпендикулярно данному вектору 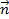 (a,b,c)
(a,b,c)
Угол между двумя плоскостями
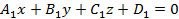
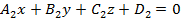 равен углу фи между нормальными векторами к этим плоскостям
равен углу фи между нормальными векторами к этим плоскостям 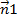 (а1.в1.с1)
(а1.в1.с1) 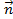 2 (а2.в2.с2)
2 (а2.в2.с2)
Параллельность, перпендикулярность совпадение
Ростояние от точки М0(х0,у0,z0) до плоскости 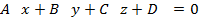
Вычесляется по формуле
Искомое уравнение 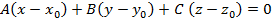
24. Уравнение прямой в пространстве.
Направляющим вектором прямой наз. любой нулевой вектор параллельны ей.
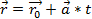 -векторная уравнение прямой
-векторная уравнение прямой
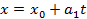
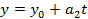 - параметрическая уравнении прямой T- параметр (число)
- параметрическая уравнении прямой T- параметр (число)
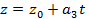
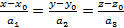 -каноническое уравнение прямой
-каноническое уравнение прямой
25. Поверхности 2-го порядка: канонические уравнения, изображение поверхностей.
26. Числовая последовательность. Виды последовательностей. Способы задания.
Числовая последовательность- это функция обозначается 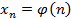 где принимает значение (1,2,3 и т.д) определенное на множество натуральных чисел
где принимает значение (1,2,3 и т.д) определенное на множество натуральных чисел
Каждое значение 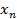 наз. элементом последовательностей число n- его номером
наз. элементом последовательностей число n- его номером
Числовая последовательность всегда содержит бесконечное множество элементов среди которых могут быть равные:
Постоянная последовательность все члены которого равны между собой
Возрастающая (убывающая) последовательность: если является возрастающай (убывающая) функция для 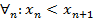
Строго монотонные - возрастающие и убывающие;монотонные – не возрастающие не убывающие
Неубывающее – если каждый элемент начиная со n≥2 не меньше предыдушего 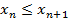
Невозрастающая - ---\\--- 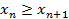
Последовательность ( 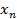 ) наз. ограниченной сверху (снизу если существует число А что
) наз. ограниченной сверху (снизу если существует число А что 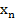 ≤ Адля любого натурального N
≤ Адля любого натурального N
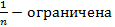 ,
, 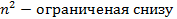
Способы задания:
1)Аналитический,
2)табличный
3)Рекурентный-указывается первый элемент и формула для n≥1 позволяет вычислить 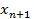 через
через 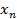
27. Пределы числовой последовательности: определение, геометрический смысл, свойство. Число е.
Число a наз. пределом числовой последовательности (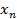 ) если для любого
) если для любого  >0 существует номер N что при
>0 существует номер N что при 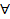 >N выполняется неравенство
>N выполняется неравенство
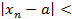 ?
?
Последовательность имеюзщая предел наз. сходящейся у которой нет предела расходящейся
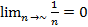
Последовательность(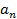 ) и (
) и (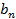 ) имеют пределы их суммы разности произведение частного существуют и находятся по формулам
) имеют пределы их суммы разности произведение частного существуют и находятся по формулам
Число е
При увелечении номера n 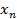 меняется все медленее можно доказать с Бинома Ньютона что это последовательность имеет придел заключенное между числпми 2 и 3 этот придел и наз. числом е
меняется все медленее можно доказать с Бинома Ньютона что это последовательность имеет придел заключенное между числпми 2 и 3 этот придел и наз. числом е

28. Предел функции в точке: определение, геометрический смысл. Односторонние пределы. Основные теоремы о пределах функции.
Теорема 1 (Первая теорема Коши)
Пусть функция ƒ (x) непрерывна на отрезке [a,b] и на концах отрезка имеет значения разных знаков, тогда существует точка  в которой ƒ (с)=0.
в которой ƒ (с)=0.
Теорема 2 Пусть функция ƒ (x) непрерывна на отрезке [a,b], причемƒ (a)=A, ƒ (b)=B, где A≠B. Тогда какое бы ни было число С, заключенное между А и B, найдется такая точка  , что ƒ (с)=С.
, что ƒ (с)=С.
29. Понятие предела функции на бесконечности. Бесконечно малые и бесконечно большие функции, их свойства. Замечательный предел.
Свойства бесконечно малых при х 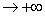 функций аналогичны свойствам бесконечно малых последовательностей.
функций аналогичны свойствам бесконечно малых последовательностей.
Теорема 1. Постоянная функция у=с является бесконечно малой при х 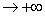 тогда и только тогда, когда с=0.
тогда и только тогда, когда с=0.
Теорема 2. Если  (х) — бесконечно малая функция при х
(х) — бесконечно малая функция при х 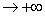 и для всех х из некоторого луча [Q,+
и для всех х из некоторого луча [Q,+ 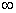 ), выполняется неравенство |
), выполняется неравенство | 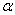 (x)|
(x)| 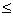 |
|  (x)|, то и
(x)|, то и 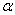 (х) есть бесконечно малая функция при х
(х) есть бесконечно малая функция при х 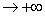 .
.
Теорема 3. Если 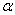 (х) — бесконечно малая функция при x
(х) — бесконечно малая функция при x 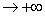 , то она является ограниченной на некотором луче [М, +
, то она является ограниченной на некотором луче [М, + 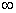 ).
).
Эти теоремы мы приводим без доказательств, так как они легко следуют из определения 1.
Теорема 4. Сумма двух бесконечно малых при х 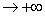 функций также является бесконечно малой при х
функций также является бесконечно малой при х 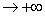 функцией.
функцией.
Теорема 5. Если 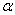 (х) — бесконечно малая при х
(х) — бесконечно малая при х 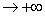 функция, а у=f(х) — ограниченная функция на некотором луче [а, +
функция, а у=f(х) — ограниченная функция на некотором луче [а, + 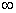 ), то их произведение является бесконечно малой при х
), то их произведение является бесконечно малой при х 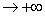 функцией.
функцией.
Следствие 1. Если 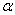 (х) — бесконечно малая при х
(х) — бесконечно малая при х 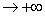 функция, то и с
функция, то и с 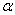 (х), где с — любое действительное число, также является бесконечно малой при х
(х), где с — любое действительное число, также является бесконечно малой при х 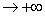 функцией.
функцией.
Следствие 2. Произведение двух (и вообще любого конечного числа) бесконечно малых при х 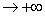 функций есть бесконечно малая при х
функций есть бесконечно малая при х 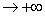 функция.
функция.
Следствие 3. Если 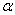 1(х),
1(х), 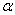 2(х),...,
2(х),..., 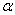 n(х)—бесконечно малые при х
n(х)—бесконечно малые при х 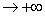 функции, то и c1
функции, то и c1 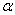 1(х) + c2
1(х) + c2 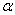 2(х) + ••• + cn
2(х) + ••• + cn 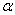 n(x) (где С1,..., Сn — действительные числа) также является бесконечно малой при х
n(x) (где С1,..., Сn — действительные числа) также является бесконечно малой при х 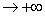 функцией.
функцией.
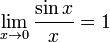
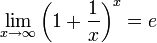 или
или 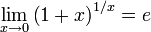
Функция y=f(x) называется бесконечно малой при x→a или при x →∞, если 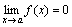 или
или 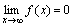 , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
, т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
30. Непрерывность функции в точке. Свойства непрерывности функции. Точка разрыва функции.
Определение 1: Функция y=f(x), определенная на интервале (а, в)
называется непрерывной в точке x0  (а, в), если
(а, в), если
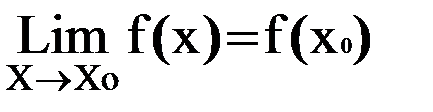 ,
,
т.е. предел функции равен ее значению при предельном значении аргумента.
Определение 2: Функция y=f(x), определенная на интервале (а, в), называются непрерывной, если для любого ε >0 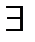 δ >0, что для любых х, удовлетворяющих условию.
δ >0, что для любых х, удовлетворяющих условию.
0<|х-a| < δ,
выполняется:
| f(x) – f(x0) | < ε
Пусть функция y= f(x) определена на интервале (а, в). Если x 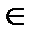 (а, в),
(а, в),
x0  (а, в), то ∆Х=Х-Х0 называется приращением аргумента в точке Х0, а ∆y=f(x)-f(x0) = f(x0 + ∆x)- f(x0) называется приращением функции в той же точке.
(а, в), то ∆Х=Х-Х0 называется приращением аргумента в точке Х0, а ∆y=f(x)-f(x0) = f(x0 + ∆x)- f(x0) называется приращением функции в той же точке.
y
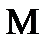
f(x)=y
f(x0)=y0 ∆y 
∆x 
0 x0 x x
Необходимое и достаточное условие непрерывности функции в точке Х0:
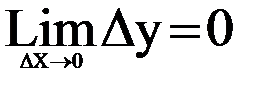
1) Доказать, что функция y=x непрерывна при любом Х=Х0
∆y=(x0+∆x)- x0 = x0+∆x-x0=∆x
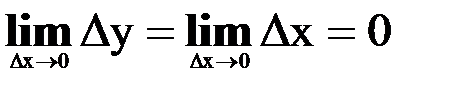
2) Доказать y = sinx непрерывна при любом х = х0
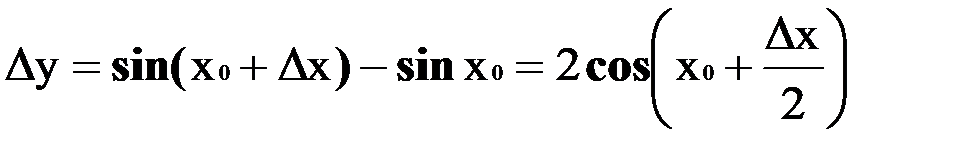 x
x
x