Арифметические действия над
Комплексными числами.
1) 
2) 
3) 
4) 
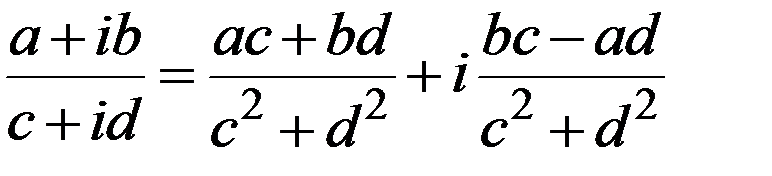
из 4) => 5)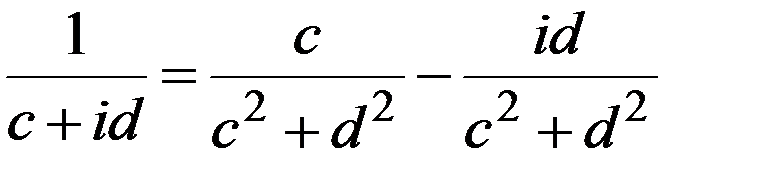 
-эта формула числа 
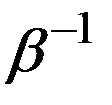, обратного числу 
Действия над комплексными числами подчиняются тем же законам, что и действия над действительными числами.
Пример:№1. Даны комплексные числа 
Найти “ + ”,
“ - ”,“ * ”, “ 
”:
“ + ” = 
“ - ” = 
“ * ” = 
“ 
” = 
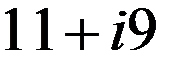
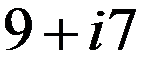
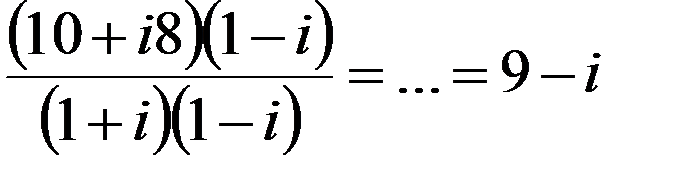
Пример: №2. Найти число, обратное 
6. Тригонометрическая форма комплексного числа, действия над числами в тригонометрической форме. Показательная форма комплексного числа.
Абсцисса a и ордината b комплексного числа a + b·i выражаются через модуль r и аргумент φ формулами Это так называемая, нормальная тригонометрическая форма, или просто, тригонометрическая форма комплексного числа.
В противоположность тригонометрической форме выражение вида a + b·i называется алгебраической или координатной формой комплексного числа.
7. Понятие матрицы, виды матриц. Линейные операции над матрицами. Транспонирование и умножение матриц.
Матрица - это таблица, состоящая из определенного количества строк и столбцов, заполненная элементами. Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера n x n называют матрицей n-го порядка.
Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.
Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной
Сложение матриц. - Суммой матриц А и В одинаковой размерности m 
n называется матрица С той же размерности, каждый элемент которой равен сумме элементов матриц А и В,
Умножение матрицы на число. Произведением матрицы на число называется матрица той же размерности, что и исходная, все элементы которой равны элементам исходной матрицы, умноженным на данное число.
|
|
Перемножение матриц.
Матрицы бывают нескольких видов
Прямоугольная
Квадратная-это матрица равная с количеством строк и столбцов
Нулевая-это матрица которые все элементы равны нулю
Диагональная-это квадратная матрица у которой все элементы не стоящие на главной диагонали равны нулю
Единичная – это Диагональная матрица у которой каждые элемент главной диагонали равен единице
Треугольная -это квадратная матрица у которой все элементы расположенные по одну сторону от главной диагонали равны нулю
Матрица столбец
8. Определители 2-го, 3-го порядка, их свойства, способы вычисления.
Пусть задана квадратная таблица из 4-х чисел:
, 
- элементы определителя
Число 
называется определителем 2-го порядка
Определителем3-го порядка, вычисляется по правилу треугольника
* * * * * *
* * * * * *
* * * * * *
Минором какого-либо элемента называется определитель, получаемый из данного определителя вычеркиванием той строки и того столбца, на пересечении которых стоит данный элемент.
Алгебраическим дополнением элемента называется его минор, взятый со своим или противоположным знаком по следующему правилу:
Если сумма номеров столбца и строки, на пересечении которых стоит элемент, есть число четное, то минор берется со своим знаком, если не четная- с противоположным.
Определитель третьего порядка равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.
|
|
9. Обратная матрица.
Обратная матрица. -это такая матрица A−1,которая при умножении на исходную матрицу A которая получает результат в единичной матрице. А также обратная матрица может существовать только в квадратной матрице
Для определение Обратной матрицы необходимо
1)Найти определитель матрицы
2)Найти алгебраические дополнения всех элементов матрицы
3)Составить союзную матрицу из алгебраических дополнений транспонированного вида
4)Разделить все элементы союзной матрицы на определитель матрицы
10. Понятие системы линейных алгебраических уравнений. Решение систем методом Крамера.
Линейной системой m уровнений с n неизвестными х1,х2…хn называется системой линейных алгебраических уравнений. Совокупность значений неизвестных, довлетворяющая всем уравнениям системы, называется решением системы. Система, имеющая хотя бы одно решение, называется совместной. Система, у которой нет решений, называется несовместной. Каждое решение совместной системы называется частным решением. Совокупность всех решений совместной системы называется общим решением. Если среди правых частей b i системы есть хоть одна, отличная от нуля, то система называется неоднородной системой линейных уравнений. Если все правые части системы равны нулю, то система называется однородной.
Метод Крамера (формулы Крамера) — способ решения систем линейных уравнений, у которых количество переменных равно количеству уравнени
Т. Если определитель системных уровнений отличен от нуля
|
|
11. Решение систем методом Гаусса
Метод Гаусса при решении системы уравнений можно разделить на два этапа: прямой и обратный ход. Вычисление неизвестных ведется в обратной последовательности: x4,x3 x2,x1. Необходимым и достаточным условием выполнения метода Гаусса должно быть следующим: все ведущие элементы Аii не должны равняться нулю