Выражают следующие теоремы:
Теорема1: Если функции f(x) и φ(x) непрерывны в точке х0, то также непрерывны в этой точке их сумма f(x)+φ(x), разность f(x)-φ(х), произведение  и частное
и частное  при условии
при условии  .
.
Т.к. непрерывные в точке х0 функции f(x) и φ(х) имеют в этой точке пределы равные f(x0) и φ(х0), то пределы суммы, разности, произведения, частного существуют и равны соответственно f(x0)+φ(x0), f(x0)-φ(х0),  ,
, 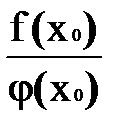 .
.
А эти величины равны значениям соответствующих функций в точке х0, следовательно функции f(x)+φ(x), f(x)-φ(х),  ,
,  непрерывны в точке х0.
непрерывны в точке х0.
Следствие1: Целая рациональная функция или  непрерывна при любых х.
непрерывна при любых х.
Следстви2: Дробная рациональная функция: 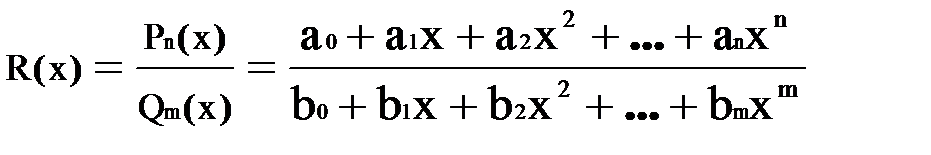
непрерывна при любых х, для которых знаменатель не равен нулю.
Теорема2: Если функция φ(х) непрерывна в точке х0, а функция f(x) непрерывна в точке y0 =φ(x0), то сложная функция F(x)=f(φ(x)), непрерывна в точке х0.
Теорема3: Все основные элементарные функции непрерывны там, где они определены.
1) Найти предел 
Решение:
Т.к. функция  непрерывна в точке
непрерывна в точке  , т.е.
, т.е.  , то переходя к пределу получаем:
, то переходя к пределу получаем:

2) 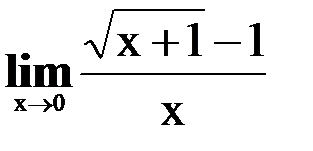
Решение:
Переходя к предельному значению аргумента, получаем неопределенность вида  .
.
f(x) не определена в точке х=0, т.е. не является непрерывной в этой точке. Значит сразу переходить к пределу нельзя, надо функцию преобразовать так, что бы при х≠0 она совпала с функцией, непрерывной в точке х0. Для этого числитель и знаменатель умножим на выражение сопряженное числителю:


Рассмотрим функцию y=f(x), определенную на интервале (а,в) кроме быть может, точки х0  (а,в)
(а,в)
Определение: Точка х0 называется, точкой разрыва данной функции, если в ней функция определена, но не является непрерывной, или не определена в этой точке.
Определение: Если х0- точка разрыва функции f(x) и существуют конечные пределы слева и справа:
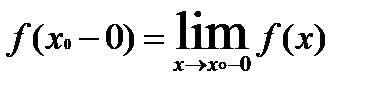 ,
, 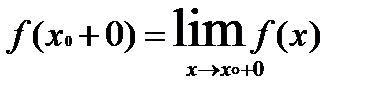 , то она называется точкой разрыва первого рода.
, то она называется точкой разрыва первого рода.
Величина  -
-  называется скачком функции в точке х0.
называется скачком функции в точке х0.
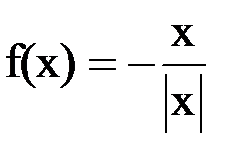
В точке х0 =0 – разрыв первого рода
В точке х0 =0 f(x)- не определена


Скачок: -2.
Определение: Если функция y=f(x) имеет разрыв в точке х0 и  =
=  , тогда х0 называется точка устранимого разрыва.
, тогда х0 называется точка устранимого разрыва.
 в точке х0 =0 – устранимый разрыв
в точке х0 =0 – устранимый разрыв
В точке х0 =0 функция не определена,

Определение: Если х0 точка разрыва и по крайней мере один из односторонних пределов слева или справа является бесконечным или не существует, то х0 называется точкой разрыва второго рода.
 х0 =0 разрыв второго рода
х0 =0 разрыв второго рода


1) 
2) 


31. Непрерывность функции на отрезке. Теоремы о непрерывностях функций.
Функция называется непрерывной на отрезке [a,b], если она непрерывна в каждой его точке (в точке a непрерывна справа, в точке b слева).
Если функция определена в точке x=a и при этом предел
 ƒ (x)=ƒ(a), то функция непрерывна справа, аналогично если
ƒ (x)=ƒ(a), то функция непрерывна справа, аналогично если
 ƒ (x)=ƒ(a), то непрерывна слева.
ƒ (x)=ƒ(a), то непрерывна слева.
Теорема 1 (Первая теорема Коши)
Пусть функция ƒ (x) непрерывна на отрезке [a,b] и на концах отрезка имеет значения разных знаков, тогда существует точка  в которой ƒ (с)=0.
в которой ƒ (с)=0.
| y |
| b |
| a |
| c |
| x |
| 0 |
Теорема 2 (Вторая теорема Коши)
Пусть функция ƒ (x) непрерывна на отрезке [a,b], причемƒ (a)=A, ƒ (b)=B, где A≠B. Тогда какое бы ни было число С, заключенное между А и B, найдется такая точка  , что ƒ (с)=С.
, что ƒ (с)=С.
| y |
| b |
| a |
| c |
| x |
| A |
| C |
| B |
| 0 |
Определение. Функция называется ограниченной на отрезке [a,b] если существует число M>0 такое, что для  выполняется неравенство | ƒ (x)≤M|.
выполняется неравенство | ƒ (x)≤M|.
| y |
| b |
| a |
| x |
| -M |
| M |
| 0 |
Теорема 3 (Первая теорема Вейерштрасса)
Если функция ƒ (x) определена и непрерывна на отрезке [a,b], то она ограничена на этом отрезке.
Замечание:
Эта теорема неверна, если отрезок [a,b] заменить интервалом (a,b). Например, ƒ (x)  - непрерывна на (0,1), но не ограничена так как
- непрерывна на (0,1), но не ограничена так как 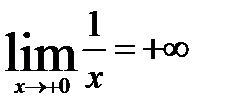 .
.
Определение. Наибольшим значением функции y= ƒ(x) на отрезке [a,b] называется такое ее значение ƒ (x), что ƒ(x)≤ ƒ(x1) при  .
.
Определение. Наименьшим значением функции y= ƒ(x) на отрезке [a,b] называется такое ее значение ƒ (x), что ƒ(x)≥ ƒ(x1) при  .
.
Теорема 4 (Вторая теорема Вейерштрасса)
Функция, непрерывная на отрезке [a,b], достигает в нем своего наименьшего m и наибольшего M значения, т.е. 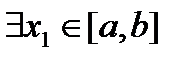 ,
,  , что ƒ(x1)=m, ƒ(x2)=M.
, что ƒ(x1)=m, ƒ(x2)=M.
| y |
| b |
| a |
| x |
| m |
| M |
| x2 |
| x1 |
| 0 |
Неубывающие и невозрастающие функции называются монотонными.
Возрастающие и убывающие функции называются строго монотонными.
Теорема 5 (О непрерывности обратной функции)
Пусть функция ƒ (x)определена, строго монотонна и непрерывна на некотором промежутке X, и пусть Y – множество ее значений. Тогда на множестве Y обратная функция  однозначна, строго монотонна и непрерывна.
однозначна, строго монотонна и непрерывна.
Например:
Функция y=sinx на 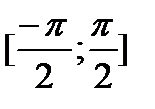 возрастает, непрерывна и множество ее значений – [-1; 1]. По теореме 5 на [-1; 1] существует непрерывная, возрастающая обратная функция со множеством значений
возрастает, непрерывна и множество ее значений – [-1; 1]. По теореме 5 на [-1; 1] существует непрерывная, возрастающая обратная функция со множеством значений 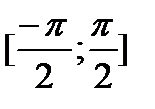 : x=arcsiny. Если теперь x и y поменять местами, т.е. рассмотреть функцию y=arcsinx, то получим график:
: x=arcsiny. Если теперь x и y поменять местами, т.е. рассмотреть функцию y=arcsinx, то получим график:
| y |
| x |
| 0 |
| -1 |
| -1 |




32. Приращение аргумента, приращение функции. Понятие производной. Физический и геометрический смысл производной.
33. Правила дифференцирования. Таблица производных. Производная сложной функции.
Функция, имеющая производную в данной точке называется дифференцируемой в данной точке.
Функция называется дифференцируемой в данном промежутке, если она имеет производную в каждой точке данного промежутка.
Если промежуток замкнутый, то на концах – односторонняя производная.
Теорема 1 (зависимость между непрерывностью и дифференцированием):
Если функция y=f(x) дифференцируема в данной точке, то она и непрерывна в ней.
Замечание: Обратное не всегда верно.
 - в точке x=1 непрерывна, но не дифференцируема.
- в точке x=1 непрерывна, но не дифференцируема.
 Пусть f(x) – дифференцируема в точке x, т.е. существует
Пусть f(x) – дифференцируема в точке x, т.е. существует  .
.
Т.к.  , то переходя к пределу
, то переходя к пределу 

Действительно функция непрерывна (по необходимому и достаточному условию непрерывности). 
Теорема 2:
Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций.
 Пусть
Пусть  , где
, где  - дифференцируемые функции.
- дифференцируемые функции.
Т.к.  ,
,
 переходя к пределу
переходя к пределу 
Таким образом,


Следствие: Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых.
Теорема 3:
Производная двух дифференцируемых функций определяется формулой

Следствие 1:
Постоянный множитель можно выносить за знак производной.
Следствие 2:
Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждой из них на остальные:
Например: 
Теорема 4:
Производная частного двух дифференцируемых функций определяется формулой
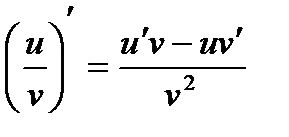
Рассмотрим сложную функцию  , где x – независимая переменная, а
, где x – независимая переменная, а  - промежуточный аргумент.
- промежуточный аргумент.
Теорема 5:
Если y=f(x) и  - дифференцируемые функции своих аргументов, то производная сложной функции
- дифференцируемые функции своих аргументов, то производная сложной функции  существует и равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
существует и равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

или

Например:

Основные формулы дифференцирования:




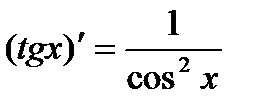




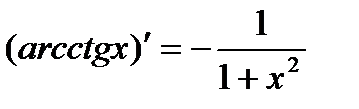


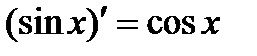

34. Основные теоремы дифференциального исчисления. Правило Лопиталя.
Ответ: Корнем или нулем функции наз. такое значение аргумента. При котором это функция обращается в нуль
Т. Роля. Между двумя различными корнями дифференцируемой функции содержаться по меньшей мере один корень ее производной
Т. Логранта. Если функция f(x) непрерывна [a,b] то существует такая точка С?(а,b) что f(b)-f(a)=f’(C)(b-a)-формула конечных приращений.
Т.Коши. Если y=f(x) и q=µ(x)- две функции непрерывны на [a, b] и дифференцируемые на интервале (а и в).При исследовании функции может проявится необходимость нахождения предела дроби f(x) и µ(х) числитель и знаменатель которой стремятся к нулю или бесконечность при х→а. Нахождение таких пределов наз. раскрытием неопределённостей соответствующего вида Основа его правила Лопиталя.
Т. Лопиталя. Если функций f(х) дефференц. В окрестности точки a x=a, обращаются в нуль этой точке и существует предел  то существует и предемл отношений самых функций равны пределу отношение производной.
то существует и предемл отношений самых функций равны пределу отношение производной.
35. Дифференциация 1-го порядка, его свойства, использование в приближенных вычислениях.
Ответ: Дифференциалом функции y=f(x) наз. произведение производной этой функции  ,dx =
,dx =  то есть дифференциал независемой переменной равен приращению dy=
то есть дифференциал независемой переменной равен приращению dy=  -формула для вычисления дифференциала. То есть производная функции равна отношению данной функции дифференциалу его аргумента
-формула для вычисления дифференциала. То есть производная функции равна отношению данной функции дифференциалу его аргумента
Свойства
1)dc=0 с-const
2)Дифференциал алгебраической суммы нескольких дифференцируемых функций равен такой же алгебраической сумме дифференциалов слагаемых d(u-v-w)=du-dv+dw
3)Дифференциал произведение двух дифференцируемых функций: d(uv)=udv+vdu
4)Дифференциал частного 
5)Дифференциал сложной функции равен произведению производной первой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента
36. Производные высших порядков. Формула Лейбница. Дифференциалы высших порядков.
Ответ: Производная от производной F(X) наз. производной второго порядка f”(x)=(f’(x))’
В случае дифференцируемости производной 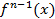 , n? N производная порядка определяется равенством.f^(n)(x)=(f^n-1(x))
, n? N производная порядка определяется равенством.f^(n)(x)=(f^n-1(x))
y=f(x)
f”(x)=(f’(x))’=d^2y/dx^2
f”’(x)=…=d^3y/dx^3
Дифференциал от дифференциала функции y=f(x) наз. дифференциалом 2 порядка
Дифференциалом n порядка наз. дифференциал от дифференциал (n-1)-го порядка.
37. Монотонность и экстремумы функций. Признак монотонности функции. Необходимое и достаточное условие экстремума.
Ответ: Монотонность функции если в данном промежутке производная функции положительная то функция возрастает на этом промежутке если отрицательная то –убывает.
Необходимое условие экстремума. Если экстремума дифференцируемой функции производная равна нулю. Так же функция может достигать экстремума в точке которой производной не существует.
1-ое достаточное условие. Если в точке х=х0 производная функции y=f(х) равна 0 и меняет знак при переходе через точку, то х0-точка экстремума, причем если х0 точка максимума, знак меняется с + на -, а если х0 точка минимума то знак меняется с минуса на плюс
2-ое достаточное условие. Если в точке х=х0 первая производная функции y=f(x) равна нулю, а вторая отлична от нуля то х0 – точка экстремума причем х0 точка минимума,если f”(x0)>0,х0 точка максимума, если f” (x0)<0
38. Выпуклость и перегиб. Асимптоты графика функции.
Ответ: График функции y=f(x) наз. Выпуклым вниз (вверх) в данном промежутке если он целиком расположен выше (ниже) касательной в его производной точке.
Признак выпуклости. Если вторая производная функции y=f(x) в данном промежутке положительна (f”(x)>0),то график ее является выпуклым вниз в этом промежутке, а если f”(x) <0, то выпуклый вверх в соответствующем промежутке
Точкой перегиба графика y=f(x) наз. такая его точка M0,в которой меняется направление выпуклости (М0 точка непрерывности функции)
Признак точки перегиба. Если в точке х=х0 2-ая производная функции y=f(x) обращается в нуль (или не существует) и меняет знак при переходе через нее, то М0 (х0,f(x0)) точка перегиба.
Асимптоты - прямые к которым неограниченно приближается данная линия, когда ее точка неограниченно удаляется от начала координат.
39. Понятие функции нескольких переменных. Линии и поверхность уровня. Предел и непрерывность ФНП.
ФНП –переменная величина z наз. функцией 2 переменных величин x и у, если в каждой паре допустимых значений (x,у) соответствует единственное значения z
Переменная величина U наз. функцией 3 переменных x,y,z, если каждой 3 паре допустимых значений.
Совокупность всех точек в которых определена ФНП наз. область определения функции.
Линии уровня функции z=f(x,y) наз. геометрическое место точек для которых данная функция имеет одно и тоже значение. F(x,y)=с уравнение линии уровня
Поверхность уровня функции 3 переменных u=f(x,y,z) наз. геометрическое место точек пространства x,y,z для которых данная функция имеет одно и тоже значение
40. Частные произведения 1-го порядка ФНП. Полный дифференциал ФНП. Частные произведение высших порядков ФНП.
Частной производной ФНП по одной из этих переменных наз. предел отношения соответствующего частного приращения функции к приращению данной переменной когда последние стремится к нулю.
При нахождении частной производной пользуется правилами дифференцирования функции одной переменной считая все другие аргументы постоянной.
Полный дифференциал ФНП- z=f(x,y) наз. главная часть полного приращения AZ,линейная относительно приращений аргументов дельта X,Y.
Частными производными высшего порядка функции z=f(x,y) наз. частные производственные от её частных производных  =
= 
Аналогично определяются частные производные третьего четвертого и высших порядков
В частности 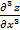 =
=  . Пробным образом определяются производные высшего порядка функции трех и более переменных
. Пробным образом определяются производные высшего порядка функции трех и более переменных
Частная производная второго порядка и выше взятая по различным переменным наз. смешанной частной производной.Если частные производные высшего порядка непрерывна то смешанные производные одного порядка не зависят от порядка дифференцирования.