Измерения величин. Вычисление погрешностей

Цель: научиться точно измерять и оценивать величины с учётом погрешностей.

Оборудование: линейка, секундомер.

Введение

Любая физическая величина может быть измерена приборами. В случае измерения длины используют, к примеру, линейку, а для измерения времени потребуется секундомер. Также есть более сложные приборы, такие как амперметр: в нём измеряется угол отклонения стрелки под действием магнитного поля или же степень деформации кристалла. Первая конструкция используется в стрелочных конструкциях, где сразу показывается сила тока. Во втором же случае внутри стоит ещё один мини-прибор, фиксирующий изменение линейных размеров кристалла, затем этот сигнал подаётся на детектор, где запрограммированы формулы для пересчёта длины в силу тока в среде данного амперметра.

Без измерений невозможно конструирование различных приборов, подтверждение или опровержение гипотез и тд. Поэтому измерения должны быть высокоточными. Измерения бывают прямыми (имеется ввиду сама величина, которую измеряют) и косвенными (посчитанные значения по измеренным прямым).

Как характеристику точности измерений вводят понятие погрешности измерения.

Погрешность измерения — вероятное отклонение измеренного значения величины от её истинного (действительного) значения.

Выяснить с абсолютной точностью истинное значение измеряемой величины, как правило, невозможно, поэтому невозможно и указать величину отклонения измеренного значения от истинного. Это отклонение принято называть ошибкой измерения.

Существует несколько классификаций погрешностей:

1. По форме представления погрешности делятся на: абсолютную погрешность — погрешность самого измерения, выражается в единицах измеряемой величины; относительную погрешность — погрешность, которая показывает отклонение от истинного значения в процентах относительно измеряемой величины.

2. По причине возникновения погрешности делятся на: приборные (из-за несовершенства прибора), методические (из-за неточности метода измерения или некоторых упрощений) и операторные (из-за человеческого фактора)

3. По характеру проявления погрешности достаточно подразделить на случайные и систематические.

Пусть длина пути от учительской до кабинета составляет 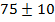метров. Здесь «75» будет являться измеренным прямым значением (путь S), а «10» — абсолютной погрешностью ( S).

Относительная погрешность определяется по формуле:

и в данном случае:

Как можно заметить, ответ был округлён до целого значения. Согласно правилам округления, если после значащей цифры стоит цифра больше 4, то число округляется с избытком: 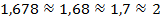, а если после значащей цифры стоит цифра меньше 5, то число округляется с недостатком: 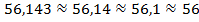. Округление приводит к неточности измеряемого или вычисляемого значения.

В случае многократных измерений вводится понятие среднего арифметического значения.

где 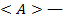среднее значение измеренной величины, 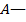измеренная величина, количество измерений.

Погрешность в таком случае будет считаться по методу Корнфельда:

В конечном итоге запись результата будет выглядеть следующим образом:

Например, при пятикратном взвешивании грузика были получены данные о массе: 4,97 кг, 5,02 кг, 4,95 кг, 5,05 кг и 4,96 кг. Средним значением массы будет являться:

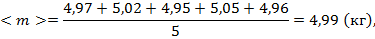
а погрешность, рассчитанная по методу Корнфельда:

В итоге записать как результат измерений необходимо:

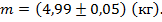
Зачастую за погрешность измеренной величины принимают половину цены деления.

Наряду с вышеизложенным способом подсчётом погрешностей (метод Корнфельда) существуют множество разных более сложных способов, о которых будет сказано позже.

В случае, когда необходимо подсчитать величину по измеренным данным с помощью графика, пользуются методом парных точек.

Также существуют правила подсчёта погрешностей косвенных измерений:

Вид функции	Формула

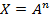
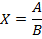
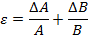
Задание

1. Определение площади парты с помощью линейки.

Линейкой измерить длину (a) и ширину (b) парты. Усреднить измеренные значения. В качестве погрешности линейки взять половину (или целую) цену деления линейки. Посчитать площадь парты (S) по формуле:

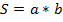
с учётом погрешности (см. таблицу погрешностей косвенных измерений). Заполнить таблицу.

a, м	b, м	, м	, м	S,	S,	, %

2. Определение площади парты с помощью пальцев.

Измерить «шагами» пальцев длину и ширину парты: выбрать одинаковое расстояние между пальцами (), измерить его линейкой, посчитать количество «шагов» в длину () и ширину (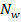) и измерить расстояние между пальцами ещё раз (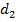). Сделать 5 измерений разными по длине «шагами». Посчитать площадь парты в каждом случае по формуле:

Вычислить погрешность методом Корнфельда. Заполнить таблицу.

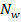
№	d, м	<d>, м					S,	S,	, %