Metal surface contacting with solution of electrolyte in some definite condition transformed to so called passive state. Study of this phenomena on the border of metal – electrolyte plays an important role, as they define the process of destruction of metal. And it is thermodynamically favourable for metal to dissolve as a result of these process. Such phenomenon was first observed by M. Faraday. This is one of the main factor of stability of metal in aggressive environment.
It is known that, there is no unified model of passivation. The most common and in first sight convincing conception of phase oxide is connecting passivation with mechanical formation of thin film on metal surface with oxide layer. However, potential of phase oxide formation differ from critical parameter of polarised curve (pic. 1), specially from potential of activation ja and passivation jП. In case of iron this difference is 0,63 v. For this reason the phase film conception of passivation cannot be taken in that from.
In case of metal passsivation determining role plays water molecule. Some part of water molecule dissociate in the process of adsorption and ion of oxygen breaking the bond with proton firmly block the most active centre of metal surface. This may be considered as start of passivation.
In the theory of passivation some physical factor must be taken in account. Most important of those are stated bellow.
1. Strong electric field. It define the transform of metal to metal oxide: 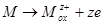 .
.
2. Equilibrium exchange on the border with solution in which take part the ion OH- and Oox .
3. Number of nonequilibrium vacancy in the passivaing oxide lattice.
4. Energetic inhomogeneity of metal surface.
Major factor of the process is inter phase difference of potential, which is defined by composition of the solution. Depending on its value the current of dissolution take the form:
| |||
 | |||
Breaks on this curve is connected with the formation of thin protection layer in sector II. Reaction of this passive layer formation is
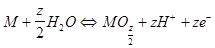
The oxygen undertakes from molecules of water, and half metal from the substrate of metal surface. As a result of formation of this layer the current falls on 4-7 orders in a very narrow interval of potential change j. After formation of a continuous monolayer there occur the state of passivity III.
The question, how this passive layer is formatted was not studied. We shall try to explain the process of passive layer formation and the kinetic of the process.
With this purpose it would be possible to use the thermodynamic theory of Gibbs- Folmer, according to which at formation of a new phase the free energy of system changes in the value  .
.
 ,
,
Where q- the geometrical factor, l- the size of the cluster, M, r- molecular weight and density of a firm phase,  - chemical potentials of supersaturated solution and firm phase with concentration C1,2 and coefficient of activity f1,2. In the point of maximum
- chemical potentials of supersaturated solution and firm phase with concentration C1,2 and coefficient of activity f1,2. In the point of maximum  the cluster is equilibrium, its critical size lkp surpasses few times the sizes of building particles (molecules) of the layer. The probability of its formation is defined by the work A of this process
the cluster is equilibrium, its critical size lkp surpasses few times the sizes of building particles (molecules) of the layer. The probability of its formation is defined by the work A of this process
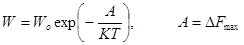 ,
,
With the condensation of the factor of crystallisation Wc, the probability of crystal cluster formation Wk is
 .
.
It is defined by the classical approaches, according to which the formation of equilibrium crystal take place by consecutive connection of building particles to the complexes, already available on surface M.
At calculation of probability it is accepted, that on the surface M spontaneously arise (or on the contrary, break up) twin crystal particles of various sizes of a and with inter nuclear distance r0. The sizes change as a result of the consecutive elementary acts (transitions) of the type such as  , i.e. growth or disintegration of crystal particles.
, i.e. growth or disintegration of crystal particles.
Probability of elementary transitions we shall designate Pa® a±r0,  . Their speeds
. Their speeds  . These values represent quantity of the acts taking place in 1 cm2 of the surface M for 1 sec. They are proportional to superficial concentration na of particles of the given size and probabilities of the elementary acts
. These values represent quantity of the acts taking place in 1 cm2 of the surface M for 1 sec. They are proportional to superficial concentration na of particles of the given size and probabilities of the elementary acts
 .
.
Resulting speed of direct and return transitions
 .
.
At balance state

Proceeding from this it is possible to find out

Further we shall define A1 and A2. Proceeding from this it is possible to calculate the speed of cluster formation

With the help of this formula it is possible to define the laws of formation of the passive layer on the sector II (in pic.1).
Then taking in to account the energetic inhomogeneity of metal surface it is possible to find out the integrated current density

where y- bond energy.
To each pair value of  corresponds the certain probability I(j, yi) of formation of twin cluster and the local degree of filling
corresponds the certain probability I(j, yi) of formation of twin cluster and the local degree of filling  by them ith platforms of the surface M. With the growth of potential j formation of cluster becomes more and more intensive. And accordingly grows the integrated degree of its filling
by them ith platforms of the surface M. With the growth of potential j formation of cluster becomes more and more intensive. And accordingly grows the integrated degree of its filling  by cluster,
by cluster,
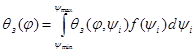
Thus the processing of the first thin superficial layer of metal in oxide is finished. Take place complete passivation of the surface M, the sector II on the curve (fig. 1) is replaced by the sector III, for which the new physical conditions must be taken in account. And further researched may be done.