Компьютерная геометрия. Двухмерные преобразования. Перемещение, масштабирование, отражение, скос с помощью матрицы 2x2.
Компьютерная геометрия есть математический аппарат, положенный в основу компьютерной графики. В свою очередь, основу компьютерной геометрии составляют различные преобразования точек и линий. При использовании машинной графики можно по желанию изменять масштаб изображения, вращать его, смещать и трансформировать для улучшения наглядности перспективного изображения. Все эти преобразования можно выполнить на основе математических методов, которые мы будем рассматривать далее.
Преобразования, как и компьютерную геометрию, разделяют на двумерные (или преобразования на плоскости) и трехмерные (или пространственные). Вначале рассмотрим преобразования на плоскости.
1. Координаты точек можно рассматривать как элементы матрицы [x,y], т. е. в виде вектор-строки или вектор-столбца.
2. Точки на плоскости xy можно перенести в новые позиции путем добавления к координатам этих точек констант переноса:

Таким образом, для перемещения точки на плоскости надо к матрице ее координат прибавить матрицу коэффициентов преобразования.
3. Рассмотрим результаты матричного умножения матрицы [x,y], определяющей точку Р, и матрицы преобразований 2x2 общего вида:

4. Масштабирование: b=c=0

5. Отражение: оу

6. Сдвиг. Координата х точки не изменяется, в то время как у* линейно зависит от начальных координат. Этот эффект называется сдвигом. Аналогично, когда a = d = 1, b = 0, преобразование осуществляет сдвиг пропорционально координате у.

Двухмерные преобразования. Вывод матрицы для поворота вокруг центра координат.
Рассмотрим умножение квадрат на матрицу преобразований.

Можно сделать вывод, что координаты В* определяются первой строкой матрицы преобразования, а координаты D* второй строкой. Зная координаты точек В* и D*, найдем матрицу преобразования. Воспользуемся этим свойством для нахождения матрицы преобразования для вращения на произвольный угол. Будем вращать единичный квадрат вокруг начала координат.


Как следует из рис, точка В с координатами (1,0) преобразуется в точку В*, для которой х*=(1)cos q и y=(1)sin q, а точка D, имеющая координаты (0,1) переходит в точку D* с координатами x*=(-1)sin q и y*=(1)cos q.
Двухмерные преобразования. Однородные координаты. Перемещение, масштабирование, вращение вокруг центра координат в однородных координатах.
1. Преобразования переноса, масштабирования и поворота записываются в матричной форме в виде: P*=P+T, P*=PxS, P*=PxR целесообразно унифицировать.
2. Переход в однородные координаты. Точки задаются вектором [x,y,1], матрица преобразований:

3. Нормализация – привидение к обычным координатам. Нормализация вектора – преобразование заданного вектора в вектор того же направления, но с единичной длиной. Длина вектора в 3Д = sqrt(x2+y2+z2).
Для 2Д. [x,y,H] = [x,y,1] * 
В общем случае Н не равно 1 и преобразованные обычные координаты получаются за счет нормализации однородных координат
x*=X/H y*=Y/H [x*,y*,1]=[X/H, Y/H, 1]
Матрицы преобразований для однородных координат.
Перенос: 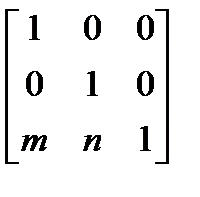
Поворот:

Масштаб: [1,1]=a, [2,2]=b, [3,3]=1 остальные 0 * 