Сформировать предварительный список приоритетов по глубине, используя в качестве ключа сортировки значение z min для каждого многоугольника. Первым в списке будет многоугольник с минимальным значением z min. Этот многоугольник лежит дальше всех от точки наблюдения, расположенной в бесконечности на положительной полуоси z. Обозначим его через P, а следующий в списке многоугольник - через Q. Для каждого многоугольника P из списка надо проверить его отношение с Q.
Если ближайшая вершина Р (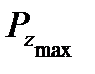
) будет дальше от точки наблюдения, чем самая удаленная вершина Q (
), т. е. 
≥ 
никакая часть P не может экранировать Q. Занести Р в буфер кадра (см. Ошибка! Источник ссылки не найден., а).
Если 
< 
, то Р потенциальное экранирует не только Q, но также и любой другой многоугольник типа Q из списка, для которого < . Тем самым образуется множество { Q }. Однако Р может фактически и не экранировать ни один из этих многоугольников. Если последнее верно, то Р можно заносить в буфер кадра. Для ответа на этот вопрос используется серия тестов, следующих по возрастанию их вычислительной сложности. Эти тесты ниже формулируются в виде вопросов. Если ответ на любой вопрос будет положительным, то Р не может экранировать { Q }. Поэтому Р сразу же заносится в буфер кадра. Вот эти тесты:
¨ Верно ли, что прямоугольные объемлющие оболочки Р и Q не перекрываются по х?
¨ Верно ли, что прямоугольные оболочки Р и Q не перекрываются по у?
¨ Верно ли, что Р целиком лежит по ту сторону плоскости, несущей Q, которая расположена дальше от точки наблюдения (рис. 27.1, а)?
¨ Верно ли, что Q целиком лежит по ту сторону плоскости, несущей P, которая ближе к точке наблюдения (рис. 27.1, b)?
¨ Верно ли, что проекции Р и Q не перекрываются?
| z |
| x |
| z |
| x |
| P |
| Q |
| P |
| Q |
| b |
| a |
Рис. 27.1. Тесты для перекрывающихся многоугольников
Каждый из этих тестов применяется к каждому элементу { Q }. Если ни один из них не дает положительного ответа и не заносит Р в буфер кадра, то Р может закрывать Q.
Поменять Р и Q местами, пометив позицию Q в списке. Повторить тесты с новым списком. Это дает положительный результат для сцены с Ошибка! Источник ссылки не найден., b.
Если сделана попытка вновь переставить Q, значит, обнаружена ситуация циклического экранирования (см. рис. 26.1). В этом случае Р разрезается плоскостью, несущей Q, исходный многоугольник Р удаляется из списка, а его части заносятся в список. Затем тесты повторяются для нового списка. Этот шаг предотвращает зацикливание алгоритма.
Алгоритм Варнака.
Алгоритм Варнока является одним из примеров алгоритма, основанного на разбиении картинной плоскости на части, для каждой из которых исходная задача может быть решена достаточно просто.
Поскольку алгоритм Варнока нацелен на обработку картинки, он работает в пространстве изображения. В пространстве изображения рассматривается окно и решается вопрос о том, пусто ли оно, или его содержимое достаточно просто для визуализации. Если это не так, то окно разбивается на фрагменты до тех пор, пока содержимое фрагмента не станет достаточно простым для визуализации или его размер не достигнет требуемого предела разрешения.
Кратко опишем оригинальную версию алгоритма, предложенного Варноком.
Разобьем видимую часть картинной плоскости на четыре равные части и рассмотрим, каким образом могут соотноситься между собой проекции граней получившейся части картинной плоскости.
Возможны четыре различных случая:
Рис. 28.1. Соотношение проекции грани с подокном
1. Проекция грани полностью накрывает область (рис. 28.1, d);
2. Проекция грани пересекает область, но не содержится в ней полностью (рис. 28.1, с);
3. Проекция грани целиком содержится внутри области (рис. 28.1, b);
4. Проекция грани не имеет общих внутренних точек с рассматриваемой областью (рис. 28.1, a).
Очевидно, что в последнем случае грань вообще никак не влияет на то, что видно в данной области.
Сравнивая область с проекциями всех граней, можно выделить случаи, когда изображение, получающееся в рассматриваемой области, определяется сразу:
¨ Проекция ни одной грани не попадает в область.
¨ Проекция только одной грани содержится в области или пересекает область. В этом случае проекции грани разбивают всю область на две части, одна из которых соответствует этой проекции.
¨ Существует грань, проекция которой полностью накрывает данную область, и эта грань расположена к картинной плоскости ближе, чем все остальные грани, проекции которых пересекают данную область. В данном случае область соответствует этой грани.
Если ни один из рассмотренных трех случаев не имеет места, то снова разбиваем область на четыре равные части и проверяем выполнение этих условий для каждой из частей. Те части, для которых таким образом не удалось установить видимость, разбиваем снова и т. д.
Естественно, возникает вопрос о критерии, на основании которого прекращать разбиение. В качестве очевидного критерия можно взять размер области. Как только размер области станет не больше размера одного пикселя, то производить дальнейшее разбиение не имеет смысла и для данной области ближайшая к ней грань определяется явно, как в методе трассировки лучей.
Иногда, для устранения лестничного эффекта, процесс разбиения проводится до размеров, меньших, чем разрешение экрана, на один пиксель. При этом усредняются атрибуты подпикселей, чтобы определить атрибуты самих пикселей.
При помощи изложенного алгоритма можно удалить либо невидимые линии, либо невидимые поверхности. Однако простота критерия разбиения, а также негибкость способа разбиения приводят к тому, что количество подразбиений оказывается велико. Можно повысить эффективность этого алгоритма, усложнив способ и критерий разбиения. На рис. 28.2, а показан другой общий способ разбиения и дано его сравнение с изложенным ранее жестким способом, представленным на рис. 28.2, b.
Рис. 28.2. Способы разбиения окна
Разбиение, показанное на рис. рис. 28.2, а, получается с использованием прямоугольной объемлющей оболочки многоугольника. Заметим, что оболочки при этом могут быть неквадратными. Этот способ можно рекурсивно применить к любому многоугольнику, который полностью охвачен каким-нибудь окном или оболочкой. Если в окне содержится только один многоугольник и если он целиком охвачен этим окном, то его легко изобразить, не проводя дальнейшего разбиения. Такой способ разбиения полезен, в частности, при минимизации числа разбиений для простых сцен. Однако с ростом сложности сцены его преимущество сходит на нет.