Проекторы. Проекции. Виды проекций.

В общем случае проекции преобразуют точки, заданные в системе координат размерностью n, в системы координат размерностью меньше чем n.

Проекция трехмерного объекта (представленного в виде совокупности точек) строится при помощи прямых проекционных лучей, которые называются проекторами и которые проходят через каждую точку объекта и, пересекая картинную плоскость, образуют проекцию.

Полная классификация проекций приведена на рис. 12.1.

Рис. 12.1. Классификация проекций

Параллельные проекции делятся на два типа в зависимости от соотношения между направлением проецирования и нормалью к проекционной плоскости (рис. 12.2):

1) ортографические – направления совпадают, т. е. направление проецирования является нормалью к проекционной плоскости;

2) косоугольные – направление проецирования и нормаль к проекционной плоскости не совпадают.

Рис. 12.2. Ортографические и косоугольные проекции

Наиболее широко используемыми видами ортографических проекций является вид спереди, вид сверху(план) и вид сбоку, в которых картинная плоскость перпендикулярна главным координатным осям. Если проекционные плоскости не перпендикулярны главным координатным осям, то такие проекции называются аксонометрическими (то есть кп не совпадает с координатной плоскостью предмета.

Изометрическая проекция – нормаль к проекционной плоскости, составляет равные углы с каждой из главных координатных осей.

Свойство: все три главные координатные оси одинаково укорачиваются, угол между ними 120°.

Рис. 12.3. Изометрическая проекция единичного куба

Косоугольные (наклонные) проекции сочетают в себе свойства ортографических проекций (видов спереди, сверху и сбоку) со свойствами аксонометрии. В этом случае проекционная плоскость перпендикулярна главной координатной оси, поэтому сторона объекта, параллельная этой плоскости, проецируется так, что можно измерить углы и расстояния. Проецирование других сторон объекта также допускает проведение линейных измерений (но не угловых) вдоль главных осей. Отметим, что нормаль к проекционной плоскости и направление проецирования не совпадают.

Двумя важными видами косоугольных проекций являются проекции:

· Кавалье (cavalier) – горизонтальная косоугольная изометрия (военная перспектива);

· Кабине (cabinet) – фронтальная косоугольная диметрия.

ПроекцияКабине (рис. 12.5) имеет направление проецирования, которое составляет с проекционной плоскостью угол = arctg(½) (≈26,5°). При этом отрезки, перпендикулярные проекционной плоскости, после проецирования составляют ½ их действительной длины. Проекции Кабине являются более реалистическими, чем проекции Кавалье, так как укорачивание с коэффициентом ½ больше согласуется с нашим визуальным опытом.

Центральнаяпроекция любой совокупности параллельных прямых, которые не параллельны проекционной плоскости, будет сходиться в точке схода. Точек схода бесконечно много. Если совокупность прямых параллельна одной из главных координатных осей, то их точка схода называется главной точкой схода. Имеются только три такие точки, соответствующие пересечениям главных координатных осей с проекционной плоскостью. Центральные проекции классифицируются в зависимости от числа главных точек схода, которыми они обладают, а следовательно и от числа координатных осей, которые пересекают проекционную плоскость.

1. Одноточечнаяпроекция (Ошибка! Источник ссылки не найден.).

2. Двухточечнаяпроекция (рис. 12.6) широко применяется в архитектурном, инженерном и промышленном проектировании.

Рис. 12.6. Двухточечная перспектива

3. Трехточечныецентральные проекции почти совсем не используются, во-первых, потому, что их трудно конструировать, а во-вторых, из-за того, что они добавляют мало нового с точки зрения реалистичности по сравнению с двухточечной проекцией.

13. Получение центральной одноточечной проекций с помощью матрицы преобразования 4x4 (два варианта).

Вариант 1. Каждую из проекций можно описать матрицей 4´4. Этот способ оказывается удобным, поскольку появляется возможность объединить матрицу проецирования с матрицей преобразования.

Центральная (перспективная)проекция получается путем перспективного преобразования и проецирования на некоторую двухмерную плоскость «наблюдения». Перспективная проекция на плоскость Z = 0 обеспечивается преобразованием

[X Y Z H] = [x y z 1 ]* = [x y 0 (rz+ 1 )].

Рис. 13.1. Вычисление одноточечной перспективы

x* = = ;

y* = = ;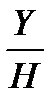

z* = = ,

где r = .

Центр проекции находится в точке с координатами ( 0,0 ,-k) (рис. 13.1), плоскость проецирования Z = 0. Соотношения между x, y и x*, y* остаются теми же самыми. Рассматривая подобные треугольники, получим, что

= , или x* = ;аналогично y* = .

Координаты x*, y* являются преобразованными координатами. В перспективном проектировании преобразованное пространство не является евклидовым, так как ортогональность осей не сохраняется. При k = ¥ получим аксонометрическое преобразование.

Аффинное преобразование есть комбинация линейных преобразований, сопровождаемых переносом. Последний столбец в обобщенной матрице 4´4 должен быть равен:

,

в этом случае H = 1.

Перспективному преобразованию может предшествовать произвольная последовательность аффинных преобразований. Таким образом, чтобы получить перспективные изображения из произвольной точки наблюдения вначале используют аффинные преобразования, позволяющие сформировать систему координат с осью Z вдоль желаемой линии визирования. Затем применяется перспективное преобразование.

Вариант 2. Аналогично перспективное преобразование, когда картинная плоскость перпендикулярна оси Z и совпадает с плоскостью Z = 1/ r. Центр проекции находится в центре координат:

[X Y Z H] = [x y z 1 ] * = [x y z (rz+ 1 )] — одноточечная перспектива (точка схода Z);

— точка схода X.