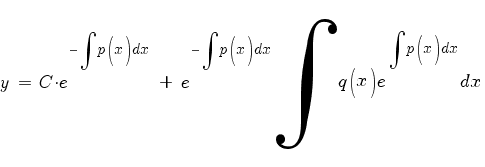Определение дифференциального уравнения. Понятие общего решения и частного решения.
Дифференциальное уравнение – уравнение, связывающее независимую переменную x и y, y’, y’’,…,y(n)
Общий вид:
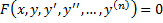
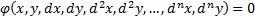
Решение ДУ – всякая функция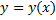 
, которая, при подстановке в ДУ, обращает ДУ в тождество.
При этом график функции 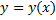называется интегральной кривой.
Общее решение уравнения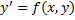 
это функция 
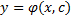, удовлетворяющая следующим условиям:
1. 
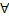C 
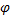обращает 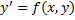в тождество
2. 
, 
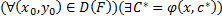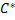удовлетворяет данным условиям, при этом 
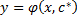- частное решение.
По Степанову:
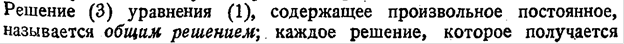
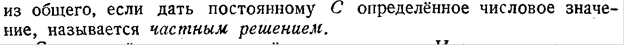
Уравнения с разделяющимися переменными.
(*)
(*): 
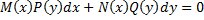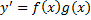
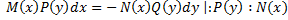
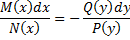
Получим
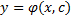или 
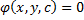при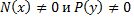 
Затем проверим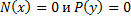 
Пусть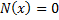 
при x=b, тогда x=b – частное решение.
Пусть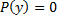 
при y=a, тогда y=a – частное решение.
Однородные уравнения и уравнения, приводящие к однородным.
По Степанову:
Проверка уравнения на однородное
В исходное уравнение: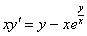 
вместо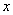 
подставляем 
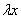, вместо 
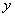подставляем 
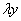, производную не трогаем:
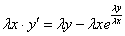
Буква лямбда – это некоторый абстрактный числовой параметр, дело не в самих лямбдах, и не в их значениях, а дело вот в чём:
Если в результате преобразований удастся сократить ВСЕ «лямбды» (т.е. получить исходное уравнение), то данное дифференциальное уравнение является однородным.
Очевидно, что лямбды сразу сокращаются в показателе степени:
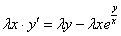
Теперь в правой части выносим лямбду за скобки:
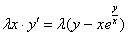
Обе части уравнения можно сократить на эту самую лямбду:
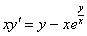
В результате все лямбды исчезли как сон, как утренний туман, и мы получили исходное уравнение.
Вывод: Данное уравнение является однородным.
Приведение к уравнению с разделяющимися переменными
Однородное уравнение приводится к уравнению с разделяющимися переменными путем замены y=tx, где t-функция, зависящая от x.
|
|
Уравнения, приводимые к однородным
К однородным уравнениям первого порядка приводится уравнение вида:
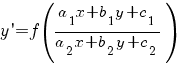
Как определить, что дифференциальное уравнение приводится к однородному
Для того, чтобы определить, что дифференциальное уравнение приводится к однородному, нужно выделить две линейные формы:
a 1 x + b 1 y + c 1, a 2 x + b 2 y + c 2, и выполнить замену:
a 1 x + b 1 y + c 1 → t(a 1 x + b 1 y + c 1);
a 2 x + b 2 y + c 2 → t(a 2 x + b 2 y + c 2)
Если после преобразований t сократится, то это уравнение приводится к однородному.
Решение дифференциального уравнения, приводящегося к однородному уравнению
Решаем систему уравнений:
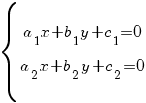
Здесь возможны три случая:
1) Система имеет бесконечное множество решений (прямые a 1 x + b 1 y + c 1 = 0 и a 2 x + b 2 y + c 2 = 0совпадают). В этом случае
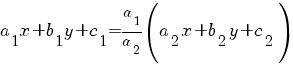
Тогда
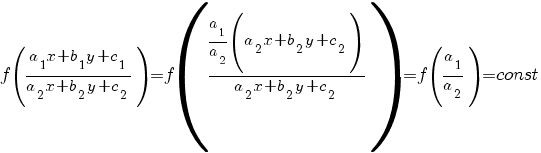
Это простейший вид уравнения с разделяющимися переменными:
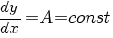
Его решение:
2) Система не имеет решений (прямые a 1 x + b 1 y + c 1 = 0 и a 2 x + b 2 y + c 2 = 0 параллельны). В этом случае a 1 b 2 – a 2 b 1 = 0;
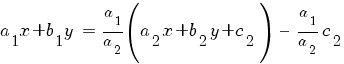
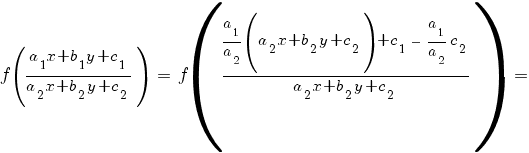
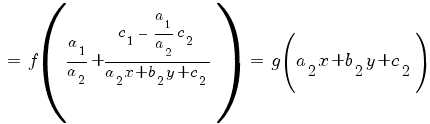
Это уравнение приводится к уравнению с разделяющимися переменными подстановкой
z = a 2 x + b 2 y + c 2.
3) Система имеет одно решение (прямые a 1 x + b 1 y + c 1 = 0 и a 2 x + b 2 y + c 2 = 0 пересекаются в одной точке). Обозначим это решение x 0, y 0. Тогда
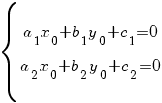
Делаем подстановку x = t + x 0, y = u + y 0. Тогда dx = dt, dy = du,
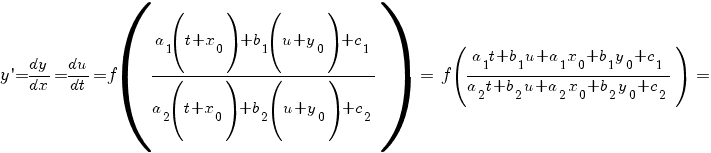
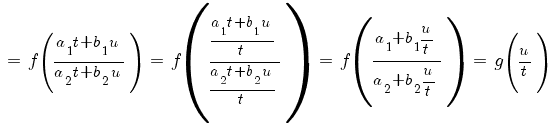
или
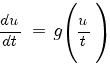
Это однородное дифференциальное уравнение первого порядка. Оно решается подстановкой u = zt, где z - функция от t.
Линейные уравнения первого порядка.
Решение линейного дифференциального уравнения с помощью интегрирующего множителя
|
|
Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:
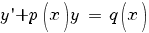
Существует три способа решения этого уравнения:
- метод интегрирующего множителя;
- метод введения двух функций (Бернулли);
- метод вариации постоянной (Лагранжа).
Рассмотрим метод решения линейного дифференциального уравнения первого порядка с помощью интегрирующего множителя.
Умножим исходное уравнение на интегрирующий множитель -
:
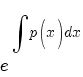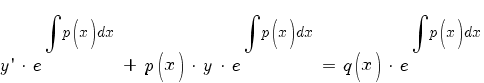
| (1) |
Далее замечаем, что производная от интеграла равна подынтегральной функции:
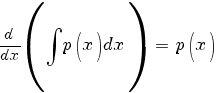
По правилу дифференцирования сложной функции:
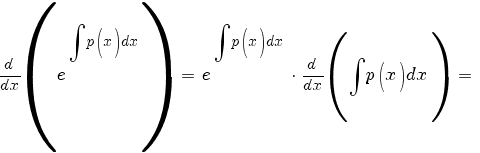
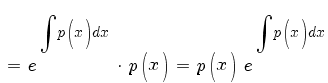
По правилу дифференцирования произведения:
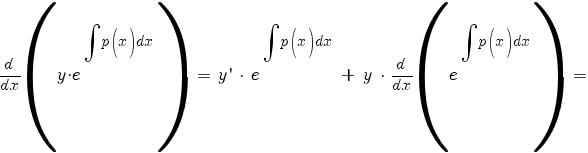
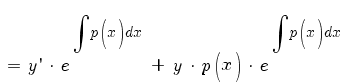
Подставляем в (1):
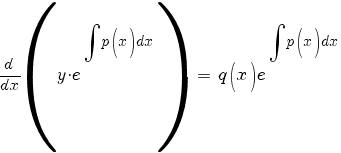
Интегрируем:
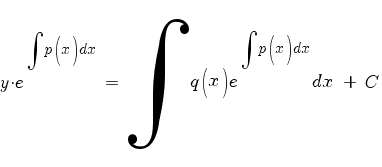
Умножаем на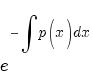 
. Получаем общее решение линейного дифференциального уравнения первого порядка:
