Ищем решение исходного уравнения в виде произведения двух функций:
y = u·v
где u, v - функции от x. Дифференцируем:
y' = u'·v + u·v'
Подставляем в исходное уравнение:

Выносим u за скобки:
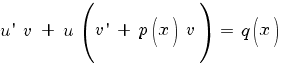
| (1) |
В качестве v возьмем любое, отличное от нуля, решение уравнения:
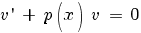
| (2) |
Это уравнение с разделяющимися переменными
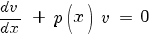
Разделяем переменные - умножаем на dx, делим на v:

Интегрируем:

Постоянную C возьмем равной нулю, поскольку нам нужно любое, отличное от нуля, решение. Тогда

Потенцируем и опускаем знак модуля (это сводится к умножению на постоянную ±1)
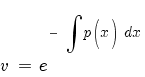
Подставим в (1) учитывая, что согласно (2) выражение в скобках равно нулю:

Отсюда

Интегрируем

Окончательно находим:


Метод вариации постоянной (Лагранжа)
Ищем решение однородного уравнения:

Это уравнение с разделяющимися переменными

Разделяем переменные - умножаем на dx, делим на y:
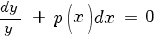
Интегрируем:

Интеграл по y - табличный:

Тогда

Потенцируем:
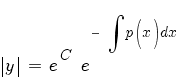
Заменим постоянную e C на C и уберем знак модуля, что сводится к умножению на постоянную ±1, которую включим в C:

| (1) |
Теперь считаем, что постоянная C является функцией от x:

Находим производную:

По правилу дифференцирования сложной функции:


По правилу дифференцирования произведения:


Подставляем в исходное уравнение:

Два члена сокращаются. Отсюда

Интегрируем:
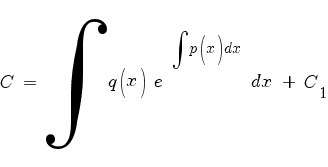
Где C 1 - постоянная интегрирования. Подставляем в (1):

Заменим постоянную C 1 на C. В результате получаем общее решение линейного дифференциального уравнения первого порядка:

Уравнение Бернулли.

Дифференциальное уравнение Бернулли – это уравнение вида

Решение дифференциального уравнения Бернулли приведением к линейному уравнению
Исходное уравнение:

| (1) |
Разделим на yn. При y ≠ 0 имеем

Это уравнение сводится к линейному с помощью замены переменной:

По правилу дифференцирования сложной функции

Подставляем:
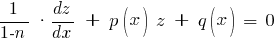
Или:

Это линейное относительно z дифференциальное уравнение. После его решения следует рассмотреть случай y = 0. При n > 0, y = 0 также является решением уравнения и должно входить в ответ.
Решение методом Бернулли
Рассматриваемое уравнение можно решить методом Бернулли. Для этого ищем решение исходного уравнения в виде произведения двух функций:

где u, v - функции от x. Дифференцируем:

Подставляем в исходное уравнение (1):


| (2) |
В качестве v возьмем любое, отличное от нуля, решение уравнения:

| (3) |
Уравнение (3) - это уравнение с разделяющимися переменными. После того, как мы нашли его частное решение v = v(x), подставляем его в (2). Поскольку оно удовлетворяет уравнению (3), то выражение в круглых скобках обращается в нуль. Получаем:

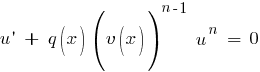
Это также уравнение с разделяющимися переменными. Находим его общее решение, а вместе с ним и решение исходного уравнения y = uv.
Уравнение Риккати.
В Степанове оказалось очень много и сложно, поэтому из него не стал приводить.
Дифференциальное уравнение Риккати – это уравнение вида

Общее решение этого уравнения можно получить только в некоторых частных случаях.