В этом случае исходное уравнение:
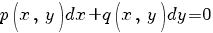
разбиваем на сумму слагаемых:

Пусть первое слагаемое имеет интегрирующий множитель:
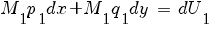
Умножаем уравнение на M1:


Далее следует подобрать такую функцию φ(U1) от U1, чтобы при умножении на нее, второе слагаемое стало полным дифференциалом:

Первое слагаемое при этом остается полным дифференциалом:

Тогда:
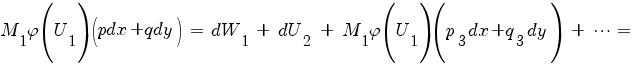

Далее следует подобрать такую функцию φ2(W1+U2) от W1+U2, чтобы при умножении на нее, следующее слагаемое стало полным дифференциалом. И так далее, пока все выражение станет полным дифференциалом.
Определение интегрирующего множителя заданного вида
В предыдущем примере мы для уравнения
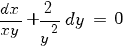
методом подбора угадали интегрирующий множитель вида M(xy):
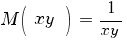
На самом деле процедуры подбора можно избежать. Можно точно определить, имеется ли для заданного уравнения интегрирующий множитель заданного вида. И если имеется, то определить его.
Пусть имеется уравнение:
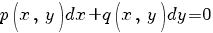
для которого ищется интегрирующий множитель вида:
M = M(u)
где u = u(x, y) - заданная функция переменных x, y.
Найдем интегрирующий множитель, или определим, что множителя такого вида не существует.
Умножим исходное уравнение на M:

Это уравнение будет уравнением в полных дифференциалах при выполнении условия:

Или:
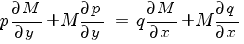

Теперь положим, что M - функция от u, где u = u(x, y) - заданная функция переменных x, y. Тогда:
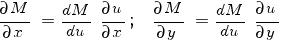
Подставляем:

Отсюда:

Интегрирующий множитель заданного вида существует, если правая часть является функцией от u:

Тогда:

Или:

Интегрируем:
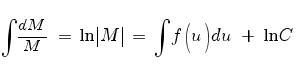
Отсюда:

Поскольку постоянная C для интегрирующего множителя никакого значения не имеет, положим C = 1:

Теорема Коши о существовании и единственности решения задачи дифференциального уравнения первого порядка.
См. Степанова. Более адекватного доказательства я не нашел.
Метод последовательных приближений.
Пусть требуется найти решение 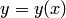 дифференциального уравнения
дифференциального уравнения

| (1) |
удовлетворяющее начальному условию

| (2) |
Будем предполагать, что в некотором прямоугольнике  с центром в точке
с центром в точке  для уравнения (1) выполнены условия а) и б) теоремы существования и единственности решения задачи (1)-(2).
для уравнения (1) выполнены условия а) и б) теоремы существования и единственности решения задачи (1)-(2).
Решение задачи (1)-(2) может быть найдено методом последовательных приближений, который состоит в следующем.
Строим последовательность  функций, определяемых рекуррентными соотношениями
функций, определяемых рекуррентными соотношениями

| (3) |
В качестве нулевого приближения  можно взять любую функцию, непрерывную в окрестности точки
можно взять любую функцию, непрерывную в окрестности точки  , в частности
, в частности 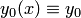 — начальное значение Коши (2). Можно доказать, что при сделанных предположениях относительно уравнения (1) последовательные приближения
— начальное значение Коши (2). Можно доказать, что при сделанных предположениях относительно уравнения (1) последовательные приближения  сходятся к точному решению уравнения (1), удовлетворяющему условию (2), в некотором интервале
сходятся к точному решению уравнения (1), удовлетворяющему условию (2), в некотором интервале 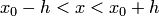 , где
, где

| (4) |
Оценка погрешности, получаемой при замене точного решения  n-м приближением
n-м приближением  , даётся неравенством
, даётся неравенством

| (5) |
где 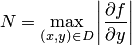 . Применяя метод последовательных приближений, следует остановиться на таком
. Применяя метод последовательных приближений, следует остановиться на таком 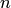 , для которого
, для которого 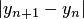 не превосходит допустимой погрешности.
не превосходит допустимой погрешности.
Следствия из теоремы Коши.
Опять же Степанов.
Принцип сжатых отображений.
Особые точки и особые решения.