Мы находимся на поверхности Земли, нам кажется, что Солнце вращается вокруг Земли, а не Земля вокруг своей оси, поэтому мы не можем отследить место положение Земли относительно Солнца или точно определить место положение Солнца относительно Земли. Помимо вращения вокруг своей оси Мы движемся с одинаковой скоростью вместе с Землей и падаем (под действием сил притяжения притягиваемся к Солнцу) на Солнце вместе с ней, поэтому эту скорость мы не ощущаем.
Почему брезентовый верх автомобиля раздувает при быстрой езде?
Уравнение Бернулли
p+pv*2/2=const
Так как сверху есть скорость, а снизу нет, то снизу появляется избыточное давление, и брезент раздувается.
Билет 3.
Относительность движения. Закон сложения скоростей в классической механике.
Движение любого тела есть движение относительное. Это значит, что движение данного тела может быть различным по отношению к другим телам.
Тело отсчета – тело, относительно которого рассматривается движение.
Закон сложения скоростей: если тело движется относительно некоторой системы отсчета K1 со скоростью V1 и сама система отсчета K1 движется относительно другой системы отсчета K2 со скоростью V2, то скорость тела относительно системы отсчета K2 равна геометрической сумме скоростей V1 и V2(проекции скоростей складываются алгебраически).
Относительная скорость – скорость материальной точки относительно подвижной системы отсчета.
Переносная скорость - скорость передвижения второй системы отсчета относительно первой.
Абсолютная скорость – скорость относительно неподвижной системы отсчета.
Получите уравнение Бернулли. Сформулируйте и докажите теорему Торричелли.
|
|
Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:
Где,
p— плотность жидкости,
v— скорость потока,
h— высота, на которой находится рассматриваемый элемент жидкости,
p— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,
g— ускорение свободного падения
Теорема Торричелли – связывает скорость истечения жидкости из малого отверстия в открытом сосуде с высотой жидкости над отверстием[1].
Формула Торричелли утверждает, что скорость 
истечения жидкости через отверстие в тонкой стенке, находящееся в ёмкости на глубине 
от поверхности, такая же, как и у тела, свободно падающего с высоты [2], то есть
где 
– ускорение свободного падения.
Легче ли побить спортивные рекорды на экваторе, нежели в более высоких широтах?
Сила тяжести, действующая на тела на экваторе, меньше той, которая действует в более высоких широтах, т.к. от экватора к полюсам ускорение свободного падения изменяется от 9,78 м/с^2 до 9,83 м/с^2 => на экваторе поставить мировой рекорд будет легче
Маленький железный предмет подпрыгнет, если к нему поднести сверху магнит. Сколько бы мы ни проводили этот опыт, сила магнита не ослабевает и он вновь и вновь совершает работу. Не противоречит ли это закону сохранения энергии?
Нет, это не противоречит закону сохранения энергии, т.к. совершаемая работа для возвращения всего в первоначальное состояние равна работе магнитных сил, которые потребовались для поднятия шарика на высоту, т.е. магнитные силы магнита не будут ослабевать, т.к. все будет возвращаться к первоначальному состоянию каждый раз.
|
|
Билет 4.
1. Движение тела, брошенного под углом к горизонту. Уравнения движения и графики x (t), y (t), vx (t), vy (t), ax (t), ay (t). Уравнение траектории y (x). Максимальная высота, время и дальность полета тела, брошенного с земли под углом к горизонту.
Пусть тело бросили под углом к горизонту, тогда
(ур. 1.)
Время полета:
(при y=0)
Дальность полета:
(подставим t0 в x)
Максимальная высота:
(подставим t0/2)
Уравнение траектории:
(выразим из ур. 1)
(подставим в ур.1)
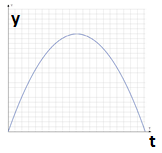
Это уравнение является уравнением траектории движения. Видно, что это уравнение параболы.
