Центром масс системы материальных точек, называют точку положение которой характеризует распределение масс этой системы.
Координаты центра масс:


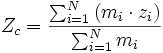
Если совокупность материальных точек является твёрдым телом, то положение центра масс в системе отсчета связанной с этим телом не изменяется.
Центр тяжести механической системы – это точка относительно которой суммарный момент сил тяжести действующих на систему равен нулю.
Центр тяжести совпадает с центром масс в однородном гравитационном поле. Т.к. в однородном гравитационном поле g(ускорение свободного падения) не изменяется.
Почему не стоит при прополке сорняков выдергивать их из земли рывком?
Из-за того, что корни сорняка запутаны и находятся под землей, если вырывать их рывком, то стебли могут порваться, а сорняк останется в земле. Рассмотрим стебли сорняка как нить, корни в земле как тяжелый шарик, и подвесим этот тяжелый шарик к потолку. Если резко потянуть, то оборвется только нижняя нить, т.к. усилие не успеет передаться на верхнюю нить так, чтобы она оборвалась. А если тянуть медленно, постепенно увеличивая прикладываемую силу, то порвется верхняя нить, т.к. на нее будут действовать сила тяжести шарик и сила приложенная к нижней нити. Так же и с сорняками: если резко потянуть, порвутся стебли, а если постепенно увеличивать усилие, то получится выдернуть сорняк.
Гитару вынесли на мороз. Ее струны натянулись сильнее, значит, увеличилась их упругая энергия. За счет чего произошло это увеличение?
При укорачивании струны из-за изменения внутренней энергии (понижение температуры способствует уменьшению кинетической энергии молекул, в следствии чего расстояние между ними уменьшается=> уменьшается внутренняя энергия и длинна струны уменьшается) увеличивается коэффициент жесткости, как у пружины при уменьшении ее длины. Следовательно энергия при оттягивании струны на ту же длину L должна стать больше (E=(k*(L)^2)/2), где k-коэффициент жесткости струны).
Билет 6.
Движение точки по криволинейной траектории. Понятие радиуса кривизны траектории. Нормальное и тангенциальное ускорение. Метод вычисления радиуса кривизны траектории тела, брошенного под углом к горизонту.
При криволинейном движении вектор скорости всегда направлен по касательной к траектории движения. Любое криволинейное движение можно представить в виде суммы прямолинейных движений и движений по окружностям разных радиусов. Скорость изменяется как по величине, так и по направлению. Вектор ускорения направлен под углом к вектору скорости.

Радиус кривизны R траектории в точке A — радиус окружности, по дуге которой точка движется в данный момент времени. При этом центр этой окружности называется центром кривизны.
Нормальное ускорение (центростремительное) определяется изменением скорости по направлению.

Тангенсальное ускорение (касательное) ускорение определяется изменением скорости по времени.
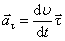
Метод вычисления радиуса кривизны:
Траектория движения в данном случае описывается уравнениями на координатных осях: х = f(t), y = f(t), где t – время, в момент которого требуется найти радиус. Вычисление радиуса кривизны будет основываться на применении формулы аn = V²/R.
Vx = x', Vy = y'.
V = √(Vx² + Vy²).
аn = √(а² - ак²)
ак = |dV/dt|
ах = х'', аy = y''.
Модуль ускорения а = √(ах2 + аy2)
R = V²/ аn