Коэффициент корреляции, равный 0,9075, показывает, что выявлена весьма тесная зависимость между общей суммой доходов населения за год и оборотом розничной торговли за год. Коэффициент детерминации, равный 0,824, устанавливает, что вариация оборота розничной торговли на 82,4% из 100% предопределена вариацией общей суммы доходов населения; роль прочих факторов, влияющих на розничный товарооборот, определяется в 17,6%, что является сравнительно небольшой величиной.
7.Для оценки статистической надёжности выявленной зависимости дохода от доли занятых рассчитаем фактическое значение F -критерия Фишера – Fфактич . и сравним его с табличным значением – Fтабл. По результатам сравнения примем решения по нулевой гипотезе 
, то есть, либо примем, либо отклоним её с вероятностью допустить ошибку, которая не превысит 5% (или с уровнем значимости α=0,05).
В нашем случае, 
. Фактическое значение критерия показывает, что факторная вариация результата почти в 33 раза больше остаточной вариации, сформировавшейся под влиянием случайных причин. Очевидно, что подобные различия не могут быть случайными, а являются результатом систематического взаимодействия оборота розничной торговли и общей суммы доходов населения. Для обоснованного вывода сравним полученный результат с табличным значением критерия: 
при степенях свободы d.f.1=k-1=1 и d.f.2=n-k=9-2=7 и уровне значимости α=0,05.
Значения 
представлены в таблице «Значения F -критерия Фишера для уровня значимости 0,05 (или 0,01)». См. приложение 1 данных «Методических указаний…».
В силу того, что 
, нулевую гипотезу о статистической незначимости выявленной зависимости оборота розничной торговли от общей суммы доходов населения и её параметрах можно отклонить с фактической вероятностью допустить ошибку значительно меньшей, чем традиционные 5%.
|
|
8. Определим теоретические значения результата Yтеор. Для этого в полученное уравнение последовательно подставим фактические значения фактора X и выполним расчёт.
Например, 
. См. гр. 5 расчётной таблицы. По парам значений Yтеор. и Xфакт. строится теоретическая линия регрессии, которая пересечётся с эмпирической регрессией в нескольких точках. См. график 1.
9. Оценку качества модели дадим с помощью скорректированной средней ошибки аппроксимации:
.
В нашем случае скорректированная ошибка аппроксимации составляет 10,2%. Она указывает на невысокое качество построенной линейной модели и ограничивает её использование для выполнения точных прогнозных расчётов даже при условии сравнительно небольшого изменения фактора X (относительно его среднего значения 
).
 |
График 1
10. Построение логарифмической функции предполагает предварительное выполнение процедуры линеаризации исходных переменных. В данном случае, для преобразования нелинейной функции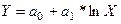 
в линейную введём новую переменную 
, которая линейно связана с результатом. Следовательно, для определения параметров модели 
будут использованы традиционные расчётные приёмы, основанные на значениях определителей второго порядка. См. расчётную таблицу №4.
Расчётная таблица №4
| № | 
| 
| 
| 
| 
| 
| 
| 
| 
|
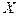
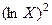
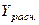
| А | |||||||||
| 11,6 | 2,451 | 7,3 | 6,007 | 17,892 | 7,0 | 0,3 | 0,1 | 2,4 | |
| 14,8 | 2,695 | 9,3 | 7,261 | 25,060 | 9,3 | 0,0 | 0,0 | 0,4 | |
| 19,0 | 2,944 | 14,0 | 8,670 | 41,222 | 11,6 | 2,4 | 5,8 | 17,9 | |
| 19,1 | 2,950 | 9,4 | 8,701 | 27,727 | 11,6 | -2,2 | 4,8 | 16,6 | |
| 26,2 | 3,266 | 15,6 | 10,665 | 50,946 | 14,6 | 1,0 | 1,0 | 7,6 | |
| 27,5 | 3,314 | 12,1 | 10,984 | 40,102 | 15,0 | -2,9 | 8,4 | 21,8 | |
| 30,0 | 3,401 | 16,3 | 11,568 | 55,440 | 15,8 | 0,5 | 0,3 | 3,4 | |
| 37,3 | 3,619 | 16,7 | 13,097 | 60,437 | 17,9 | -1,2 | 1,4 | 8,8 | |
| 39,5 | 3,676 | 20,5 | 13,515 | 75,364 | 18,4 | 2,1 | 4,4 | 15,5 | |
| Итого | 28,316 | 121,2 | 90,468 | 394,190 | 121,2 | 0,0 | 26,2 | 94,2 | |
| Средняя | 3,146 | 13,5 | — | — | — | — | 2,9 | 10,5 | |
| Сигма | 0,391 | 4,04 | |||||||
| Дисперсия, D | 0,153 | 16,29 |
Расчёт определителей второго порядка даёт следующие результаты:
|
|
; 
; 
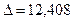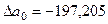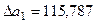. Отсюда получаем параметры уравнения:
Полученное уравнение имеет вид: 
.
Оценочные показатели позволяют сделать вывод, что линейно-логарифмическая функция описывает изучаемую связь хуже, чем линейная модель: оценка тесноты выявленной связи ρ=0,9066 (сравните с 0,9075), скорректированная средняя ошибка аппроксимации здесь выше и составляет 10,5%, то есть возможности использования для прогноза данной модели более ограничены.
Таким образом, можно придти к выводу, что по сравнению с линейной моделью данное уравнение менее пригодно для описания изучаемой связи.
11. Выполним расчёт параметров уравнения параболы второго порядка. В этом случае используются определители третьего порядка, расчёт которых выполняется по стандартным формулам и требует особого внимания и точности. См. расчётную таблицу 5
По материалам табл. 5 выполним расчёт четырёх определителей третьего порядка по следующим формулам:
Δ = n*Σx2*Σx4 + Σx*Σx3*Σx2 + Σx*Σx3*Σx2 – Σx2*Σx2*Σx2 – Σx*Σx*Σx4 – Σx3*Σx3*n =
= 331.854.860,7;
Δa0 = Σy*Σx2*Σx4 + Σx*Σx3*Σ(y*x2)+ Σ(y*x)*Σx3*Σx2 – Σ(y*x2)*Σx2*Σx2 –
- Σ(y*x)*Σx*Σx4 – Σx3*Σx3*Σy = 751.979.368,8
Δa1 = n*Σ(y*x)*Σx4 + Σy*Σx3*Σx2 + Σx*Σ(y*x2)*Σx2 – Σx2*Σ(y*x)* Σx2 – Σx*Σy* Σx4 -
|
|
- Σ(y*x2)*Σx3*n = 167.288.933,1
Δa2 = n*Σx2*Σ(y*x2) + Σx*Σyx*Σx2 + Σx*Σx3*Σy – Σx2*Σx2*Σy – Σx*Σx*Σ(y*x2) –
- Σx3*Σ(y*x)*n = - 656.926,8
В результате получаем следующие значения параметров уравнения параболы:
; 
; 
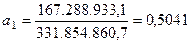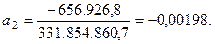
Уравнение имеет следующий вид: 
. Для него показатель детерминации составляет 82,7%, Fфактич. = 14,3, а ошибка аппроксимации 
10,7%.
Как видим, по сравнению с линейной функцией построить уравнения параболы гораздо сложнее, а изучаемую зависимость она описывает почти с той же точностью, хотя надёжность уравнения параболы значительно ниже (для линейной модели Fфактич. = 32,8,а для параболы Fфактич.= 14,3). Поэтому в дальнейшем анализе парабола второго порядка использоваться не будет.
Расчётная таблица №5
| № |
|
| 
| 
| 
| 
| 
|
|
|
|
|
| А | |||||||||||
| 11,6 | 7,3 | 84,7 | 6,007 | 17,892 | 18106,4 | 982,3 | 7,8 | -0,5 | 0,3 | 4,1 | |
| 14,8 | 9,3 | 137,6 | 7,261 | 25,060 | 47978,5 | 2037,1 | 9,3 | 0,0 | 0,0 | 0,1 | |
| 14,0 | 266,0 | 8,670 | 41,222 | 130321,0 | 5054,0 | 11,1 | 2,9 | 8,4 | 21,3 | ||
| 19,1 | 9,4 | 179,5 | 8,701 | 27,727 | 133086,3 | 3429,2 | 11,2 | -1,8 | 3,2 | 13,2 | |
| 26,2 | 15,6 | 408,7 | 10,665 | 50,946 | 471199,9 | 10708,5 | 14,1 | 1,5 | 2,3 | 11,0 | |
| 27,5 | 12,1 | 332,8 | 10,984 | 40,102 | 571914,1 | 9150,6 | 14,6 | -2,5 | 6,3 | 18,8 | |
| 16,3 | 489,0 | 11,568 | 55,440 | 810000,0 | 14670,0 | 15,6 | 0,7 | 0,5 | 5,1 | ||
| 37,3 | 16,7 | 622,9 | 13,097 | 60,437 | 1935687,9 | 23234,5 | 18,3 | -1,6 | 2,6 | 12,0 | |
| 39,5 | 20,5 | 809,8 | 13,515 | 75,364 | 2434380,1 | 31985,1 | 19,1 | 1,4 | 2,0 | 10,5 | |
| Итого | 121,2 | 3331,0 | 90,468 | 394,190 | 6552674,1 | 101251,3 | 121,2 | 0,0 | 25,6 | 96,0 | |
| Средняя | 25,0 | 13,5 | — | — | — | — | — | — | — | 2,8 | 10,7 |
| Сигма | 9,12 | 4,04 | |||||||||
| D | 83,18 | 16,29 |
12. Проведём расчёт параметров степенной функции, которому также предшествует процедура линеаризации исходных переменных. В данном случае выполняется логарифмирование обеих частей уравнения, в результате которого получаем уравнение, где линейно связаны значения логарифмов фактора и результата. Исходное уравнение 
после логарифмирования приобретает следующий вид: 
. Порядок расчёта приведён в таблице 6.
Расчётная таблица №6
| № |
|
|
| 
|
| 
| 
| 
|
|
|
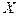
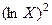
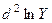
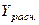
| А | ||||||||||
| 11,6 | 7,3 | 2,4510 | 1,9879 | 4,8723 | 4,8723 | 2,0330 | 0,0020 | 7,6 | 2,5 | |
| 14,8 | 9,3 | 2,6946 | 2,2300 | 6,0091 | 6,0091 | 2,2148 | 0,0002 | 9,2 | 1,0 | |
| 19,0 | 14,0 | 2,9444 | 2,6391 | 7,7705 | 7,7705 | 2,4011 | 0,0566 | 11,0 | 22,0 | |
| 19,1 | 9,4 | 2,9497 | 2,2407 | 6,6094 | 6,6094 | 2,4050 | 0,0270 | 11,1 | 12,5 | |
| 26,2 | 15,6 | 3,2658 | 2,7473 | 8,9719 | 8,9719 | 2,6408 | 0,0113 | 14,0 | 11,7 | |
| 27,5 | 12,1 | 3,3142 | 2,4932 | 8,2629 | 8,2629 | 2,6770 | 0,0338 | 14,5 | 18,1 | |
| 30,0 | 16,3 | 3,4012 | 2,7912 | 9,4933 | 9,4933 | 2,7419 | 0,0024 | 15,5 | 5,8 | |
| 37,3 | 16,7 | 3,6190 | 2,8154 | 10,1889 | 10,1889 | 2,9044 | 0,0079 | 18,3 | 11,5 | |
| 39,5 | 20,5 | 3,6763 | 3,0204 | 11,1040 | 11,1040 | 2,9471 | 0,0054 | 19,1 | 10,8 | |
| Итого | 121,2 | 28,3162 | 22,9651 | 73,2824 | 73,2824 | 22,9651 | 0,1467 | 120,3 | 96,0 | |
| Средняя | 13,5 | 3,1462 | 2,5517 | — | — | — | — | — | 10,7 | |
| Сигма | 0,3914 | 0,3187 | ||||||||
| D | 0,1532 | 0,1016 |
В результате расчёта получены следующие значения определителей второго порядка:
12,4075;
2,5371;
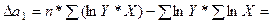9,25642.
Параметры степенной функции составляют:
; 
.
Уравнение имеет вид: lnY=ln a0 + a1*ln X = 0,2045 + 0,7460*X, а после процедуры потенцирования уравнение приобретает окончательный вид:
или 
.
Полученное уравнение несколько лучше описывает изучаемую зависимость и более надёжно по сравнению с линейной моделью. Степенная модель имеет детерминацию на уровне 84,0% (против 82,4% по линейной модели), Fфакт. =36,6 (против 33,1 для линейной модели) и ошибку аппроксимации на уровне 10,7% (сравните с 10,9% для уравнения прямой).
Очевидно, что преимущества степенной модели по сравнению с линейной не столь значительны, но её построение заметно сложнее и требует значительно больших усилий. Поэтому окончательный выбор, в данном конкретном случае, сделаем в пользу модели, которая является более простой при построении, анализе и использовании, то есть в пользу линейной модели:
Заключительным этапом решения данной задачи является выполнение прогноза и его оценка.
Если предположить, что прогнозное значение общей суммы доходов населения, например, Новгородской области, (см. табл.2 строка 2) возрастёт с 14,8 млрд. руб.на 5,7% и составит 15,6 млрд. руб., то есть 
Xпрогнозн.= 14,8*1,057=15,6, тогда прогнозное значение результата сформируется на уровне: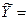 
Yпрогнозн. =3,415+0,402*15,6=9,7 (млрд. руб.). То есть, прирост фактора на 5,7% приводит к приросту результата на 4,2 процента (
.
Рассчитаем интегральную ошибку прогноза - 
, которая формируется как сумма двух ошибок: из ошибки прогноза как результата отклонения прогноза от уравнения регрессии- 
и ошибки прогноза положения регрессии - 
. То есть,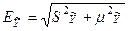 
.
В нашем случае 
, где k- число факторов в уравнении, которое в данной задаче равно 1. Тогда 
(млрд. руб.).
Ошибка положения регрессии составит: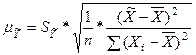 
=
= 
= 
= 0,914 (млрд. руб.).
Интегральная ошибка прогноза составит: =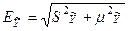 
= 2,1 (млрд. руб.).
Предельная ошибка прогноза, которая не будет превышена в 95% возможных реализаций прогноза, составит: 
= 2,365*2,1 = 5,011 ≈ 5,0 (млрд. руб.). Табличное значение t -критерия для уровня значимости α=0,05 и для степеней свободы n-k-1 = 9-1-1=7 составит 2,365. (См. табл. приложения 2). Следовательно, ошибка большинства реализаций прогноза не превысит 
млрд. руб.
Это означает, что фактическая реализация прогноза будет находиться в доверительном интервале 
. Верхняя граница доверительного интервала составит
= 9,7 + 5,0 = 14,7(млрд. руб.).
Нижняя граница доверительного интервала составит:
= 9,7 - 5,0 = 4,7(млрд. руб.).
Относительная величина различий значений верхней и нижней границ составит: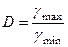 
= 
раза. Это означает, что верхняя граница в 3,12 раза больше нижней границы, то есть точность выполненного прогноза весьма невелика, но его надёжность на уровне 95% оценивается как высокая. Причиной небольшой точности прогноза является повышенная ошибка аппроксимации. Здесь её значение выходит за границу 5-7% из-за недостаточно высокой типичности линейной регрессии, которая проявляется в присутствии единиц с высокой индивидуальной ошибкой. Если удалить территории с предельно высокой ошибкой (например, Калининградскую область с 
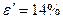), тогда качество линейной модели и точность прогноза по ней заметно повысятся.
Задача №2.
Выполняется изучение социально-экономических процессов в регионах Южного федерального округа РФ по статистическим показателям за 2000 год.
Y – оборот розничной торговли, млрд. руб.;
X1 – инвестиции 2000 года в основной капитал, млрд. руб.;
X2 – средний возраст занятых в экономике, лет
X3 – среднегодовая численность населения, млн. чел.
Требуется изучить влияние указанных факторов на оборот розничной торговли.
Предварительный анализ исходных данных по 12 территориям выявил наличие двух территорию (Краснодарский край и Ростовская обл.) с аномальными значениями признаков. Эти территории должны быть исключены из дальнейшего анализа. Значения приводимых показателей рассчитаны без учёта указанных аномальных единиц.
При обработке исходных данных получены следующие значения:
А) - линейных коэффициентов парной корреляции, средних и средних квадратических отклонений -σ:
N=10.
| 
| 
| 
| |
|
| 0,7938 | 0,2916 | 0,8891 | |
|
| 0,7938 | 0,2994 | 0,6693 | |
|
| 0,2916 | 0,2994 | 0,0113 | |
|
| 0,8891 | 0,6693 | 0,0113 | |
| Средняя | 8,878 | 5,549 | 38,79 | 1,160 |
| 8,7838 | 5,1612 | 1,0483 | 0,90107 |
Б) - коэффициентов частной корреляции
|
|
|
|
| |
|
| 0,4726 | 0,5169 | 0,8511 | |
|
| 0,4726 | 0,0521 | -0,0793 | |
|
| 0,5156 | 0,0521 | -0,5598 | |
|
| 0,8511 | -0,0793 | -0,5598 |
Задание:
1. По значениям линейных коэффициентов парной и частной корреляции выберите неколлинеарные факторы и рассчитайте для них коэффициенты частной корреляции. Произведите окончательный отбор информативных факторов во множественную регрессионную модель.
2. Выполните расчёт бета коэффициентов (b) и постройте с их помощью уравнение множественной регрессии в стандартизованном масштабе. Проанализируйте с помощью бета коэффициентов (b) силу связи каждого фактора с результатом и выявите сильно и слабо влияющие факторы.
3. По значениям b -коэффициентов рассчитайте параметры уравнения в естественной форме (то есть a1, a2, и a0). Проанализируйте их значения. Сравнительную оценку силы связи факторов дайте с помощью общих (средних) коэффициентов эластичности - 
.
4. Оцените тесноту множественной связи с помощью R и R 2, а статистическую значимость уравнения и тесноту выявленной связи - через F -критерий Фишера (для уровня значимости a =0,05).