По результатам прогноза по параболе численность занятого населения в ближайшие годы будет постепенно возрастать, достигая 64 – 65 млн. чел.
Задача №7.
Данные о стоимости экспорта (
) и импорта (
) Франции, млрд. $, приводятся за период с 1991 по 2000 г.
В уровнях рядов выявлены линейные тренды:
для экспорта - 
, а для импорта – 
.
По указанным трендам произведено выравнивание каждого ряда, то есть рассчитаны теоретические значения их уровней: 
и 
| Годы | Экспорт ()
| Импорт ()
| ||
 .
|
| 
|
| |
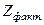
Предварительная обработка исходной информации привела к следующим результатам:
| Mt | Zt | t | |
| Mt | 0,9606 | 0,8836 | |
| Zt | 0,9606 | 0,8629 | |
| T | 0,8836 | 0,8629 | |
| Итого | |||
| Средняя | 266,6 | 260,7 | 5,5 |
| 35,579 | 30,845 | 2,872 |
Задание:
1. Для изучения связи рядов рассчитайте отклонения фактических значений каждого ряда от теоретических (
и 
);
2. Для оценки тесноты связи рассчитайте: 1) линейный коэффициент парной корреляции отклонений от линии тренда: 
; 2) уровней рядов: 
и 3) коэффициент частной корреляции уровней: 
; поясните их значения, укажите причины различий значений парных коэффициентов корреляции (пп. 1 и 2) и схожести коэффициентов парной корреляции отклонений и частной корреляции уровней (пп.1 и 3);
3. Постройте уравнение множественной регрессии с участием временной с 
4. Проанализируйте полученные результаты.
Решение.
1. Изучение связи рядов выполним двумя способами, сравним их результаты и выберем из них правильный. Для оценки тесноты связи рядов через величины отклонений от оптимального тренда рассчитаем значения отклонений: 
и 
(см. табл. 1)
|
|
Таблица 1.
| Годы |
| 
|
| 
| 
| 
| 
| 
| 
|
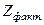
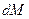
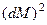
| -31 | -36 | ||||||||
| -14 | -17 | ||||||||
| -5 | -35 | ||||||||
| -4 | -3 | ||||||||
| -21 | -1 | ||||||||
| Итого | — | — | |||||||
| Средняя | 266,6 | — | 260,7 | — | — | 283,6 | 248,8 | ||
| Сигма | 35,58 | — | 30,84 | — | 16,84 | 15,77 | — | — | — |
| D | 1265,84 | — | 951,41 | — | 283,60 | 248,80 | — | — | — |
Выполним расчёт коэффициента корреляции отклонений от трендов через коэффициент регрессии отклонений с1, 
и 
. Но для этого предварительно рассчитаем определители второго порядка по уравнению регрессии отклонений: 
.
В силу того, что свободный член уравнения регрессии отклонений равен нулю, вид уравнения будет отличаться от традиционного: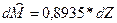 
. С изменением отлонений импорта от своего тренда на единицу отклонения экспорта от своего тренда изменятся в том же направлении на 0,8935 часть своей единицы. В дальнейшем коэффициент с1 используется для расчёта показателей тесноты связи двух рядов отклонений:
; 
Выявлена тесная связь отклонений от трендов, которая означает, что на 70,0% вариация размеров отклонений по импорту детерминирует изменения по экспорту, а на 30% вариация размеров отклонений происходит под влиянием прочих факторов.
|
|
Второй вариант оценки связи двух рядов основан на традиционной оценке корреляции их уровней:
.
Данный подход к решению задачи предполагает традиционный расчёт определителей уравнения регрессии уровней, нахождение коэффициента регрессии а1 и далее с помощью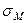 
и 
расчёт коэффициента корреляции. Информация для расчёта представлена в табл. 2.
Расчёт определителей дал следующие результаты:
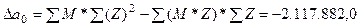
Значения параметров регрессии: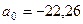 
; 
, а уравнение имеет вид:
.
Коэффициенты тесноты связи уровней составят: 
; 
. Это значит, что в уровнях существует весьма тесная связь, при которой вариации импорта предопределяет 92,2% вариации экспорта.
Таблица 2.
| Годы |
|
| 
| 
| 
|
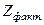
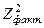
| Итого | |||||
| Средняя | 266,6 | 260,7 | |||
| Сигма | 35,58 | 30,84 | |||
| D | 1265,84 | 951,41 |
2. Однако, делать подобный вывод было бы глубоко ошибочно потому, что в уровнях и одного, и другого рядов выявлены устойчивые, статистически значимые линейные тренды. В подобных условиях выявленное взаимодействие уровней не является причинной зависимостью, а представляет собой ложную связь, вызванную наличием трендов схожей линейной формы. В силу того, что оба тренда сформированы под влиянием разного комплекса факторов, схожесть их формы могут создавать иллюзию связи рядов. Подобные соображения позволяют отказаться от результатов изучения связи уровней, содержащих тренд. В подобной ситуации пристального внимания заслуживает связь случайных отклонений от трендов. Именно этот подход позволяет выявить и количественно оценить истинную связь рядов.
|
|
В действительности связь рядов существует, оценивается она как тесная; то есть, в ней экспорт на 70% детерминирован вариацией импорта. Фактический F -критерий равен 18,9. Это больше табличного (F табл.= 5,32), что доказывает надёжность и значимость истинной связи рядов.
3. Для формализованного представления подобных зависимостей и использования моделей связи динамических рядов в прогнозных расчётах предлагается построить множественную регрессионную модель связи рядов, включая в неё в качестве обязательной составляющей фактор времени t. Речь идёт о построении модели следующего вида: 
. В данной задаче в уровнях обоих рядов присутствует линейный тренд. Поэтому включение в модель фактора времени позволит через коэффициент а2 отразить наличие линейного тренда в уровнях обоих рядов. Если в уровнях рядов представлены тренды иной, более сложной формы, тогда уравнение множественной регрессии должно через фактор времени отразить эту более сложную форму трендов.
Истинную силу и направление связи рядов отразит коэффициент регрессии а1 , а тесноту их связи оценит частный коэффициент корреляции: .
Используем для расчёта параметров множественной регрессии матрицу парных коэффициентов корреляции, представленную в исходных данных.
Для построения уравнения в стандартизованном масштабе: 
рассчитаем значения 
-коэффициентов:
Получено следующее уравнение: 
.
Его параметры позволяют сделать вывод о том, что влияния импорта на экспорт почти в четыре раза сильнее, чем влияние систематических факторов, формирующих линейный тренд: 
По значениям -коэффициентов рассчитаем параметры множественной регрессии в естественной форме: 
; 
.
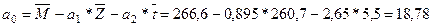Уравнение имеет вид: 
. С увеличением импорта на 1 млрд. $ экспорт увеличивается на 0,895 млрд.$; под влиянием комплекса систематических факторов (которые условно обозначили через t) экспорт увеличивается в среднем за год на 2,65 млрд. $.
Оценку тесноты связи рядов, очищенную от влияния комплекса систематических факторов, даёт частный коэффициент корреляции:
; 
.
Как видим, получены результаты, совпадающие с оценками тесноты связи по отклонениям от лучших трендов, которыми, в данном случае, являются линейные тренды.
Использование динамической модели в прогнозе заключается в подстановке в её правую часть прогнозных значений фактора Z и фактора t. То есть, 
Приложения
Приложение 1.
Таблица значений F-критерия Фишера
| k2 -степени свободы остаточной дисперсии (k2 =n-m-1) | k1 - степени свободы факторной дисперсии (k1 = m) | |||||||||||
| k1=1 | k1=2 | K1=3 | k1=4 | |||||||||
| Уровень значимости, α | ||||||||||||
| 0,10 | 0,05 | 0,01 | 0,10 | 0,05 | 0,01 | 0,10 | 0,05 | 0,01 | 0,10 | 0,05 | 0,01 | |
| 39,9 | 161,5 | 49,5 | 199,5 | 53,6 | 215,72 | 55,8 | 224,57 | |||||
| 8,5 | 18,5 | 98,5 | 9,0 | 19,0 | 99,00 | 9,2 | 19,16 | 99,2 | 19,2 | 19,25 | 99,30 | |
| 5,54 | 10,13 | 34,1 | 5,46 | 9,6 | 30,82 | 5,39 | 9,28 | 29,5 | 5,34 | 9,12 | 28,71 | |
| 4,54 | 7,71 | 21,2 | 4,32 | 6,9 | 18,00 | 4,19 | 6,59 | 16,7 | 4,11 | 6,39 | 15,98 | |
| 4,06 | 6,61 | 16,3 | 3,78 | 5,79 | 13,27 | 3,62 | 5,41 | 12,1 | 3,52 | 5,19 | 11,39 | |
| 3,78 | 5,99 | 13,8 | 3,46 | 5,14 | 10,92 | 3,29 | 4,76 | 9,8 | 3,18 | 4,53 | 9,15 | |
| 3,59 | 5,59 | 12,3 | 3,26 | 4,74 | 9,55 | 3,07 | 4,35 | 8,5 | 2,96 | 4,12 | 7,85 | |
| 3,46 | 5,32 | 11,3 | 3,11 | 4,46 | 8,65 | 2,92 | 4,07 | 7,6 | 2,81 | 3,84 | 7,01 | |
| 3,36 | 5,12 | 10,6 | 3,01 | 4,26 | 8,02 | 2,81 | 3,86 | 7,0 | 2,69 | 3,63 | 6,42 | |
| 3,29 | 4,96 | 10,0 | 2,92 | 4,10 | 7,56 | 2,73 | 3,71 | 6,6 | 2,61 | 3,48 | 5,99 | |
| 3,23 | 4,84 | 9,7 | 2,86 | 3,98 | 7,20 | 2,66 | 3,59 | 6,2 | 2,54 | 3,36 | 5,67 | |
| 3,18 | 4,75 | 9,3 | 2,81 | 3,88 | 6,93 | 2,61 | 3,49 | 6,0 | 2,48 | 3,26 | 5,41 | |
| 3,14 | 4,67 | 9,1 | 2,76 | 3,80 | 6,70 | 2,56 | 3,41 | 5,7 | 2,43 | 3,18 | 5,20 | |
| 3,10 | 4,60 | 8,9 | 2,73 | 3,74 | 6,51 | 2,52 | 3,34 | 5,6 | 2,39 | 3,11 | 5,03 | |
| 3,07 | 4,54 | 8,7 | 2,70 | 3,68 | 6,36 | 2,49 | 3,29 | 5,4 | 2,36 | 3,06 | 4,89 | |
| 3,05 | 4,49 | 8,5 | 2,67 | 3,63 | 6,23 | 2,46 | 3,24 | 5,3 | 2,33 | 3,01 | 4,77 | |
| 3,03 | 4,45 | 8,4 | 2,64 | 3,59 | 6,11 | 2,44 | 3,20 | 5,2 | 2,31 | 2,96 | 4,67 | |
| 3,01 | 4,41 | 8,3 | 2,62 | 3,55 | 6,01 | 2,42 | 3,16 | 5,1 | 2,29 | 2,93 | 4,58 | |
| 2,99 | 4,38 | 8,2 | 2,61 | 3,52 | 5,93 | 2,40 | 3,13 | 5,0 | 2,27 | 2,90 | 4,50 | |
| 2,97 | 4,35 | 7,9 | 2,59 | 3,49 | 5,72 | 2,38 | 3,10 | 4,9 | 2,25 | 2,87 | 4,31 | |
| … | 4,32 | 8,0 | … | 3,47 | 5,78 | … | 3,07 | 4,9 | … | 2,84 | 4,37 | |
| 2,95 | 4,30 | 7,9 | 2,56 | 3,44 | 5,72 | 2,35 | 3,05 | 4,8 | 2,22 | 2,82 | 4,31 | |
| … | 4,28 | 7,9 | … | 3,42 | 5,66 | … | 3,03 | 4,8 | … | 2,80 | 4,26 | |
| 2,93 | 4,26 | 7,8 | 2,54 | 3,40 | 5,61 | 2,33 | 3,01 | 4,7 | 2,19 | 2,78 | 4,22 | |
| … | 4,24 | 7,8 | … | 3,38 | 5,57 | … | 2,99 | 4,7 | … | 2,76 | 4,18 | |
| 2,91 | 4,22 | 7,7 | 25,2 | 3,37 | 5,53 | 2,31 | 2,98 | 4,6 | 2,17 | 2,73 | 4,14 | |
| 2,88 | 4,17 | 7,56 | 2,49 | 3,32 | 5,39 | 2,28 | 2,92 | 4,5 | 2,14 | 2,69 | 4,02 | |
| 2,84 | 4,08 | 7,31 | 2,44 | 3,23 | 5,18 | 2,23 | 2,84 | 4,3 | 2,09 | 2,61 | 3,83 | |
| 2,79 | 4,00 | 7,08 | 2,39 | 3,15 | 4,98 | 2,18 | 2,76 | 4,1 | 2,04 | 2,53 | 3,65 | |
| 2,77 | 8,96 | 6,96 | 2,37 | 3,11 | 4,88 | 2,16 | 2,72 | 4,0 | 2,02 | 2,48 | 3,56 | |
| 2,76 | 3,94 | 6,90 | 2,36 | 3,09 | 4,82 | 2,14 | 2,70 | 3,98 | 2,00 | 2,46 | 3,51 | |
| ∞ | 2,71 | 3,84 | 6,63 | 2,30 | 3,00 | 4,61 | 2,08 | 2,60 | 3,78 | 1,94 | 2,37 | 3,32 |
Приложение 2
Таблица критических значений t-статистики Стьюдента
| Число степеней свободы, d.f.=n-k-1 | Уровень значимости, α (двусторонний) | ||||||
| 0,40 | 0,30 | 0,20 | 0,10 | 0,05 | 0,02 | 0,01 | |
| 1,38 | 1,96 | 3,08 | 6,31 | 12,71 | 31,82 | 63,66 | |
| 1,06 | 1,39 | 1,89 | 2,92 | 4,30 | 6,97 | 9,93 | |
| 0,98 | 1,25 | 1,64 | 2,35 | 3,18 | 4,54 | 5,84 | |
| 0,94 | 1,19 | 1,53 | 2,13 | 2,78 | 3,75 | 4,60 | |
| 0,92 | 1,16 | 1,48 | 2,02 | 2,57 | 3,37 | 4,03 | |
| 0,91 | 1,13 | 1,44 | 1,94 | 2,45 | 3,14 | 3,71 | |
| 0,90 | 1,12 | 1,42 | 1,90 | 2,37 | 3,00 | 3,50 | |
| 0,89 | 1,11 | 1,40 | 1,86 | 2,31 | 2,90 | 3,36 | |
| 0,88 | 1,10 | 1,38 | 1,83 | 2,26 | 2,82 | 3,25 | |
| 0,88 | 1,09 | 1,37 | 1,81 | 2,23 | 2,76 | 3,17 | |
| 0,88 | 1,09 | 1,36 | 1,80 | 2,20 | 2,72 | 3,11 | |
| 0,87 | 1,08 | 1,36 | 1,78 | 2,18 | 2,68 | 3,06 | |
| 0,87 | 1,08 | 1,35 | 1,77 | 2,16 | 2,65 | 3,01 | |
| 0,87 | 1,08 | 1,35 | 1,76 | 2,15 | 2,62 | 3,00 | |
| 0,87 | 1,07 | 1,34 | 1,75 | 2,13 | 2,60 | 2,95 | |
| 0,87 | 1,07 | 1,34 | 1,75 | 2,12 | 2,58 | 2,92 | |
| 0,86 | 1,07 | 1,33 | 1,74 | 2,11 | 2,57 | 2,90 | |
| 0,86 | 1,07 | 1,33 | 1,73 | 2,10 | 2,55 | 2,88 | |
| 0,86 | 1,07 | 1,33 | 1,73 | 2,09 | 2,54 | 2,86 | |
| 0,86 | 1,06 | 1,33 | 1,73 | 2,09 | 2,53 | 2,85 | |
| 0,86 | 1,06 | 1,32 | 1,72 | 2,08 | 2,52 | 2,83 | |
| 0,86 | 1,06 | 1,32 | 1,72 | 2,07 | 2,51 | 2,82 | |
| 0,86 | 1,06 | 1,32 | 1,71 | 2,07 | 2,50 | 2,81 | |
| 0,86 | 1,06 | 1,32 | 1,71 | 2,06 | 2,49 | 2,80 | |
| 0,86 | 1,06 | 1,32 | 1,71 | 2,06 | 2,49 | 2,79 | |
| 0,86 | 1,06 | 1,32 | 1,71 | 2,06 | 2,48 | 2,78 | |
| 0,86 | 1,06 | 1,31 | 1,70 | 2,05 | 2,47 | 2,77 | |
| 0,86 | 1,06 | 1,31 | 1,70 | 2,05 | 2,47 | 2,63 | |
| 0,85 | 1,06 | 1,31 | 1,70 | 2,05 | 2,46 | 2,76 | |
| 0,85 | 1,06 | 1,31 | 1,70 | 2,04 | 2,46 | 2,75 | |
| 0,85 | 1,05 | 1,30 | 1,68 | 2,02 | 2,42 | 2,70 | |
| 0,85 | 1,05 | 1,30 | 1,67 | 2,00 | 2,39 | 2,66 | |
| 0,85 | 1,04 | 1,30 | 1,66 | 1,98 | 2,36 | 2,62 | |
| ∞ | 0,84 | 1,036 | 1,28 | 1,65 | 1,96 | 2,33 | 2,58 |