Показательный тренд установил, что численность занятых сокращается со среднегодовым темпом, равным 0,9825 или 98,3%. За период 1990-2001 гг. численность занятых ежегодно уменьшалась в среднем на 1,7%.
В данном случае, показатели тесноты изучаемой связи рассчитываются не как обычно – на фактических и расчётных значениях результата (
и 
), а с использованием линеаризованных значений результата 
и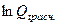 
, потому что именно для них выполняется требование МНК о наименьшей сумме квадратов отклонений. Расчёт выполнен в гр.8 и 9.
Выявлена весьма тесная зависимость численности занятых от комплекса систематических факторов: 
. Уравнение и его параметры статистически значимы и надёжны, т.к. Fфакт.= 112, что значительно превосходит Fтабл.= 5,12 (при d.f.1=1; d.f.2=11-1-1=9; α=0,05).
Средняя ошибка аппроксимации в данной задаче рассчитывается как обычно, с использованием и , т. к. при решении прогнозных задач производится оценка естественных, а не линеаризованных значений результата. Ошибка мала: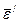 
=1,3% и поэтому модель может быть рекомендована для использования при прогнозировании. При этом, важно убедиться, что после выявления тренда формируются отклонения 
= 
, представляющие собой значения случайной переменной.
Для этого рассчитаем коэффициент автокорреляции отклонений: 
. Расчёт выполняется по линеаризованным значениям результата, то есть, с иcпользованием 
и 
.
Необходимая для расчёта информация представлена в табл. 5.
По аналогии с предыдущими расчётами определим коэффициент автокорреляции через определители второго порядка для двух рядов отклонений: и .
;
; 
;
; 
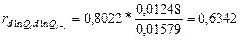Таблица 5
| (Y)
| (X)
| 
| 
| |
| 0,013 | — | — | — | |
| 0,010 | 0,013 | 0,00013 | 0,00016 | |
| 0,005 | 0,010 | 0,00005 | 0,00011 | |
| 0,006 | 0,005 | 0,00003 | 0,00002 | |
| -0,011 | 0,006 | -0,00006 | 0,00003 | |
| -0,025 | -0,011 | 0,00027 | 0,00012 | |
| -0,013 | -0,025 | 0,00032 | 0,00060 | |
| -0,015 | -0,013 | 0,00019 | 0,00017 | |
| -0,011 | -0,015 | 0,00017 | 0,00023 | |
| 0,009 | -0,011 | -0,00011 | 0,00013 | |
| 0,032 | 0,009 | 0,00030 | 0,00009 | |
| Итого | -0,013 | -0,032 | 0,00129 | 0,00166 |
| Средняя | -0,0013 | -0,0032 | — | — |
| Сигма | 0,01579 | 0,0124841 | — | — |
| D | 0,0002493 | 0,0001559 | — | — |
Отклонения от показательного тренда находятся в заметной зависимости, которая, по оценке F -критерия, является статистически значимой и надёжной: 
. Нулевая гипотеза о несущественной связи отклонений должна быть отвергнута с 5%-ой вероятностью ошибки. Это означает, что показательный тренд не является лучшим, т.к. не аккумулирует в себе влияния всего комплекса существенных факторов, а оставляет часть этого влияния в отклонениях от тренда. Поэтому показательный тренд не следует рассматривать как лучший.
4. Остановимся на порядке построения и использования степенной модели в решении поставленных задач. В данной модели реализуется концепция мультипликативного механизма воздействия фактора на результат: 
. Построению модели предшествует процедура линеаризации исходного уравнения п утём логарифмирования его элементов: 
. В расчёте параметров участвуют 
и 
. Необходимая для расчёта исходная и промежуточная информация представлена в табл. 6.
Расчёт определителей приводит к следующим результатам:
;
;
.
Значения параметров линеаризованного уравнения составят:
; 
,
а уравнение линейное в линейной форме имеет вид:
.
Таблица 6
| Годы |
|
| 
| 
| 
|
| 
|
| 0,000 | 4,321 | 0,000 | 0,000 | 4,346 | -0,025 | 0,00063 | |
| 0,693 | 4,301 | 0,480 | 2,981 | 4,291 | 0,010 | 0,00010 | |
| 1,099 | 4,278 | 1,207 | 4,700 | 4,259 | 0,019 | 0,00036 | |
| 1,386 | 4,261 | 1,922 | 5,907 | 4,236 | 0,025 | 0,00063 | |
| 1,609 | 4,227 | 2,590 | 6,803 | 4,219 | 0,008 | 0,00006 | |
| 1,792 | 4,196 | 3,210 | 7,518 | 4,204 | -0,009 | 0,00008 | |
| 1,946 | 4,190 | 3,787 | 8,153 | 4,192 | -0,002 | 0,00000 | |
| 2,079 | 4,170 | 4,324 | 8,671 | 4,182 | -0,012 | 0,00014 | |
| 2,197 | 4,156 | 4,828 | 9,131 | 4,172 | -0,016 | 0,00026 | |
| 2,303 | 4,159 | 5,302 | 9,576 | 4,164 | -0,005 | 0,00003 | |
| 2,398 | 4,164 | 5,750 | 9,984 | 4,156 | 0,007 | 0,00005 | |
| Итого | 17,502 | 46,422 | 33,400 | 73,424 | 46,422 | 0,000 | 0,00234 |
| Средняя | 1,591 | 4,220 | — | — | — | — | 0,00021 |
| Сигма | 0,710 | 0,058 | — | — | — | — | — |
| D | 0,505 | 0,0034 | — | — | — | — | — |
После процедуры потенцирования получаем уравнения в естественной форме:
или иначе 
.
В модели нашло отражение единственная тенденция устойчивого сокращения численности занятых со снижающимся темпом этого сокращения. Если использовать модель для прогноза, то это будет прогноз снижения численности занятых, но при этом, процент её (численности) сокращения год от года будет уменьшаться.
Степенная модель выявляет связь, которая оценивается как весьма тесная и статистически значимая: 
. 
.
Особо отметим, что в данном случае, так же, как и при оценке тесноты связи показательной модели, расчёты общей и остаточной дисперсий проводятся по линеаризованным значениям признака-результата, то есть по и
Расчёт ошибки аппроксимации приводится в табл. 7. Её значение очень невелико и составляет 1,7%. При отсутствии автокорреляции в отклонениях от тренда степенная модель может использоваться для прогноза без формальных ограничений.
Таблица 7.
| Годы |
| 
| 
| 
|
|
|
| 
|
| 77,2 | -1,9 | 3,6 | 2,8 | -0,025 | — | — | — | |
| 73,1 | 0,7 | 0,5 | 1,1 | 0,010 | -0,025 | -0,00025 | 0,000610 | |
| 70,8 | 1,3 | 1,7 | 2,0 | 0,019 | 0,010 | 0,00019 | 0,000101 | |
| 69,2 | 1,7 | 2,9 | 2,6 | 0,025 | 0,019 | 0,00047 | 0,000355 | |
| 67,9 | 0,6 | 0,4 | 0,8 | 0,008 | 0,025 | 0,00020 | 0,000617 | |
| 67,0 | -0,6 | 0,4 | 0,8 | -0,009 | 0,008 | -0,00007 | 0,000065 | |
| 66,2 | -0,2 | 0,0 | 0,2 | -0,002 | -0,009 | 0,00002 | 0,000074 | |
| 65,5 | -0,8 | 0,6 | 1,1 | -0,012 | -0,002 | 0,00003 | 0,000006 | |
| 64,9 | -1,1 | 1,2 | 1,6 | -0,016 | -0,012 | 0,00019 | 0,000139 | |
| 64,3 | -0,3 | 0,1 | 0,5 | -0,005 | -0,016 | 0,00008 | 0,000271 | |
| 63,8 | 0,5 | 0,3 | 0,7 | 0,007 | -0,005 | -0,00004 | 0,000025 | |
| Итого | 749,73 | 0,1 | 11,7 | 14,1 | 0,025 | -0,007 | 0,00083 | 0,002265 |
| Средняя | — | — | 1,06 | 1,3 | 0,0025 | -0,0007 | — | — |
| D | — | — | — | — | 0,01283 | 0,01503 | — | — |
В табл. 7 приводятся результаты проверки остатков на их автокоррелированность. В результате установлено, что в остатках существует умеренная связь, но она не является статистически значимой, то есть ряд отклонений представляют собой случайную переменную.
; 
; 
; 
.
Следовательно, нулевая гипотеза о статистической незначимости взаимосвязи отклонений от степенного тренда должна быть принята, при том, что вероятность допустить ошибку не превысит общепринятого 5% уровня.
Следовательно, степенной тренд отражает влияние комплекса систематических факторов и после исключения этого влияния из фактических уровней в них остаются значения, случайные по своей природе. Поэтому нет формальных ограничений на использование степенной модели в прогнозных расчётах.
5.Выполним расчёт параметров уравнения параболы второго порядка и оценим возможность её использования для выполнения прогнозов.
Значения параметров рассчитаем, используя определители третьего порядка, формулы которых приведены в решении типовой задачи №1. Необходимые данные представлены в табл. 8. В результате получены следующие значения определителей системы нормальных уравнений:
Таблица 8
| Годы | 
| 
| 
| 
| 
| 
| 
|
|
|
|
|
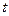
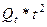
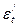
| 75,3 | 75,3 | 75,3 | 75,9 | -0,6 | 0,36 | 0,9 | |||||
| 73,8 | 147,6 | 295,2 | 73,7 | 0,1 | 0,01 | 0,1 | |||||
| 72,1 | 216,3 | 648,9 | 71,7 | 0,4 | 0,16 | 0,6 | |||||
| 70,9 | 283,6 | 1134,4 | 69,9 | 1,0 | 1,00 | 1,4 | |||||
| 68,5 | 342,5 | 1712,5 | 68,4 | 0,1 | 0,01 | 0,2 | |||||
| 66,4 | 398,4 | 2390,4 | 67,0 | -0,6 | 0,36 | 0,9 | |||||
| 66,0 | 462,0 | 65,9 | 0,1 | 0,01 | 0,1 | ||||||
| 64,7 | 517,6 | 4140,8 | 65,1 | -0,4 | 0,16 | 0,5 | |||||
| 63,8 | 574,2 | 5167,8 | 64,4 | -0,6 | 0,36 | 0,9 | |||||
| 64,0 | 640,0 | 64,0 | 0,0 | 0,00 | 0,0 | ||||||
| 64,3 | 707,3 | 7780,3 | 63,8 | 0,5 | 0,25 | 0,8 | |||||
| Итого | 749,8 | 4364,8 | 32979,6 | 749,8 | 0,0 | 2,68 | 6,5 | ||||
| Средняя | 68,2 | — | — | — | — | — | — | — | 0,24 | 0,6 | |
| Сигма | 4,01 | 3,16 | — | — | — | — | — | — | — | — | — |
| D | 16,08 | 10,0 | — | — | — | — | — | — | — | — | — |
; 
; 
; 
; 
; 
.
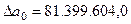Уравнение параболы второго порядка имеет вид: 
. Знак минус у коэффициента регрессии а2 указывает на то, что парабола обращена своей вершиной вниз. То есть, у параболы есть точка минимума, в которой результат принимает наименьшее значение. Достигается это минимальное значение при условии равенства нулю первой производной данной функции. В нашем примере 
или 
. Отсюда 
.
В соответствии с используемой моделью параболы второго порядка численность занятых в экономике РФ будет наименьшей в период между 11 и 12 годами, то есть в период 2000-2001 года. В этот момент численность занятых достигнет своего минимального значения в 63,8 млн. чел.:
(млн. чел.).
Начиная с этого момента, в соответствии с рассматриваемой моделью, численность занятых в экономике РФ будет постепенно увеличиваться. Проблема состоит в том, чтобы определить те временные границы, в которых рассматриваемая модель может использоваться с наибольшей результативностью, т.е. давать наиболее точные и достоверные прогнозы.
Для нас важной особенностью представляемой модели является то, что в ней реализуется гипотеза о стабилизации процесса снижения численности занятых и следующего за ним процесса постепенного увеличения контингента занятых. Но, при этом, очень важно, чтобы для модели были характерны высокие оценочные параметры.
В гр. 9, 10 и 11 представлены данные для расчёта показателей тесноты описанной параболой связи. Уравнение выявило весьма тесную связь ( 
), которая на 98,5% детерминирована системой устойчивых, статистически значимых факторов. Об этом говорит F-критерий, фактическое значение которого в десятки раз превышает его табличное значение: 
при d.f.1 =2; d.f.2 =8 при α =0,05.
Ошибка аппроксимации имеет весьма малое значение: 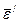=0,6%, что указывает на хорошие перспективы при использовании модели для прогнозных расчётов.
В табл. 9 представлены данные для проверки наличия автокорреляции в отклонениях фактических уровней ряда от теоретических, рассчитанных по уравнению параболы.
Рассчитаем определители для коэффициента регрессии отклонений с1 и по ним определим его значение: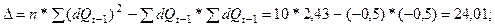 
С помощью коэффициента регрессии отклонений (с1) и значений средних квадратических отклонений каждого ряда остатков (
и 
) определим коэффициент автокорреляции:
; 
.
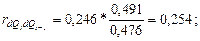
Таблица 9.
| Годы |
|
| 
|
|
|
| 77,2 | -0,6 | — | — | — | |
| 73,1 | 0,1 | -0,6 | -0,06 | 0,36 | |
| 70,8 | 0,4 | 0,1 | 0,04 | 0,01 | |
| 69,2 | 1,0 | 0,4 | 0,40 | 0,16 | |
| 67,9 | 0,1 | 1,0 | 0,10 | 1,00 | |
| 67,0 | -0,6 | 0,1 | -0,06 | 0,01 | |
| 66,2 | 0,1 | -0,6 | -0,06 | 0,36 | |
| 65,5 | -0,4 | 0,1 | -0,04 | 0,01 | |
| 64,9 | -0,6 | -0,4 | 0,24 | 0,16 | |
| 64,3 | 0,0 | -0,6 | -0,00 | 0,36 | |
| 63,8 | 0,5 | 0,0 | 0,00 | 0,00 | |
| Итого | 749,73 | 0,6 | -0,5 | 0,56 | 2,43 |
| Средняя | — | 0,06 | -0,05 | — | — |
| D | — | 0,476 | 0,491 | — | — |
Как показали расчёты коэффициента автокорреляции, отклонения от параболического тренда находятся в слабой взаимосвязи, которая не является статистически значимой, устойчивой и надёжной. То есть, парабола наилучшим образом отражает форму основной тенденции в фактических уровнях.
Кроме того, парабола способна реализовать прогноз, основанный на предположении о постепенной стабилизации численности занятых с её последующим увеличением. В качестве альтернативы может быть рассмотрен прогноз, основанный на гипотезе о снижающейся численности занятых, но с затухающими темпами этого снижения, то есть вариант стабилизирующейся численности занятых. Указанный вариант прогноза может быть выполнен либо по уравнению равносторонней гиперболы, либо по степенной модели. Окончательный выбор вариантов прогноза может быть сделан по результатам анализа оперативной информации о текущих изменениях численности занятых в экономике РФ.
Заканчиваем решение задачи выполнением прогноза по параболе второго порядка. Прогноз выполним на четыре года: на 2001 – 2004 гг. Условный фактор – фактор времени t, примет прогнозные значения, продолжающие натуральный ряд чисел, использованных для его обозначения. То есть, 
При подстановке значений 
и 
в уравнение параболы и после выполнения соответствующих расчётов получаем прогнозные значения численности занятых:
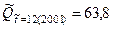млн. чел.;
млн. чел.;
млн. чел.;
млн. чел.