9. Рассчитайте интегральную и предельную ошибки прогноза (для a=0,05), определите доверительный интервал прогноза (
; 
), а также диапазон верхней и нижней границ доверительного интервала (
), оцените точность выполненного прогноза.
Задача №2.
Изучаются показатели социально-экономического развития экономики территорий Южного федерального округа РФ за 2000 год..
Y – валовой региональный продукт, млрд. руб.;
X1 – среднегодовая численность занятых в экономике, млн. чел.;
X2 – инвестиции предыдущего, 1999 года в основной капитал, млрд. руб.;
X3 – кредиты, предоставленные в предыдущем, 1999 году предприятиям, организациям, банкам и физическим лицам, млрд. руб.
Требуется изучить влияние указанных факторов на стоимость валового регионального продукта.
Предварительный анализ исходных данных по 12 территориям выявил одну территорию (Краснодарский край) с аномальными значениями признаков. Эта территория должна быть исключена из дальнейшего анализа. Значения приводимых показателей рассчитаны без учёта указанной аномальной единицы.
При обработке исходных данных получены следующие значения:
А) - линейных коэффициентов парной корреляции, средних и средних квадратических отклонений -σ:
N=11.
| Y | X1 | X2 | X3 | |
| Y | 0,9348 | 0,9578 | 0,7914 | |
| X1 | 0,9348 | 0,8696 | 0,7764 | |
| X2 | 0,9578 | 0,8696 | 0,7342 | |
| X3 | 0,7914 | 0,7764 | 0,7342 | |
| Средняя | 20,54 | 0,4995 | 3,379 | 0,2762 |
| σ | 21,85 | 0,4187 | 3,232 | 0,3159 |
Б) - коэффициентов частной корреляции
| Y | X1 | X2 | X3 | |
| Y | 0,6545 | 0,8211 | 0,2468 | |
| X1 | 0,6545 | -0,2352 | 0,1399 | |
| X2 | 0,8211 | -0,2352 | -0,0976 | |
| X3 | 0,2468 | 0,1399 | -0,0976 |
Задание:
1. По значениям линейных коэффициентов парной и частной корреляции выберите неколлинеарные факторы и рассчитайте для них коэффициенты частной корреляции. Проведите окончательный отбор информативных факторов во множественную регрессионную модель.
|
|
2. Выполните расчёт бета коэффициентов (b) и постройте с их помощью уравнение множественной регрессии в стандартизованном масштабе. Проанализируйте с помощью бета коэффициентов (b) силу связи каждого фактора с результатом и выявите сильно и слабо влияющие факторы.
3. По значениям b-коэффициентов рассчитайте параметры уравнения в естественной форме (a1, a2 и a0). Проанализируйте их значения. Сравнительную оценку силы связи факторов дайте с помощью общих (средних) коэффициентов эластичности - 
.
4. Оцените тесноту множественной связи с помощью R и R2, а статистическую значимость уравнения и тесноту выявленной связи - через F -критерий Фишера (для уровня значимости a=0,05).
5. Рассчитайте прогнозное значение результата, предполагая, что прогнозные значения факторов составят 106,7 процента от их среднего уровня.
6. Основные выводы оформите аналитической запиской.
Задача №3.
Для проверки рабочих гипотез (№1 и №2) о связи социально-экономических показателей в регионе используется статистическая информация за 2000 год по территориям Центрального федерального округа.
Y1 – среднемесячная начисленная заработная плата 1-го занятого в экономике, тыс. руб.;
Y2 – стоимость валового регионального продукта, млрд. руб.;
X1 – доля занятых в экономике в общей численности населения, %;
X2 - инвестиции текущего, 2000 года в основной капитал, млрд. руб.;
X3 - среднедушевые денежные доходы населения (в месяц), млн. руб.
Рабочие гипотезы:
Предварительный анализ исходных данных по 18 территориям выявил наличие трёх территорий (г. Москва, Московская обл., Воронежская обл.) с аномальными значениями признаков. Эти единицы должны быть исключены из дальнейшего анализа. Значения приводимых показателей рассчитаны без учёта указанных аномальных единиц.
|
|
При обработке исходных данных получены следующие значения линейных коэффициентов парной корреляции, средних и средних квадратических отклонений -σ:
N=15.
Для проверки рабочей гипотезы №1. Для проверки рабочей гипотезы №2.
| Y1 | X1 | X2 | Y2 | 
| X3 | ||
| Y1 | 0,6712 | 0,6745 | Y2 | 0,8179 | 0,6085 | ||
| X1 | 0,6712 | 0,3341 |
| 0,8179 | 0,5440 | ||
| X2 | 0,6745 | 0,3341 | X3 | 0,6085 | 0,5440 | ||
| Средняя | 1,553 | 44,23 | 5,600 | Средняя | 23,77 | 1,553 | 1,3246 |
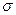
| 0,2201 | 2,1146 | 2,4666 |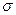
| 7,2743 | 0,2001 | 0,2123 |
Задание:
1. Составьте систему уравнений в соответствии с выдвинутыми рабочими гипотезами.
2. Определите вид уравнений и системы.
3. На основе приведённых в условии значений матриц коэффициентов парной корреляции, средних и средних квадратических отклонений:
- определите бета коэффициенты b) и постройте уравнения множественной регрессии в стандартизованном масштабе;
- дайте сравнительную оценку силы влияния факторов на результат;
- рассчитайте параметры a1, a2 и a0 уравнений множественной регрессии в естественной форме;
- с помощью коэффициентов парной корреляции и b- коэффициентов рассчитайте для каждого уравнения линейный коэффициент множественной корреляции (R) и детерминации (R2);
- оцените с помощью F -критерия Фишера статистическую надёжность выявленных связей.
4. Выводы оформите краткой аналитической запиской.
Задача 4.
|
|
Предлагается изучить взаимосвязи социально-экономических характеристик региона за период.
Y1 – среднее число детей в 1-ой семье региона, чел.
Y2 – среди населения в возрасте 18-49 лет процент лиц с полным средним образованием, %
Y3 – среднемесячная заработная плата 1-го занятого в экономике региона, тыс. руб.
X1 – среди членов семьи средний процент пенсионеров, %
X2 – приходится в среднем кв. м жилой площади на 1-го члена семьи в регионе, кв. м
X3 – инвестиции прошлого года в экономику региона, млрд. руб.
Приводится система рабочих гипотез, которые необходимо проверить.
Задание
1. Используя рабочие гипотезы, постройте систему структурных уравнений и проведите их идентификацию;
2. Укажите, при каких условиях может быть найдено решение каждого из уравнений и системы в целом. Дайте обоснование возможных вариантов подобных решений и аргументируйте выбор оптимального варианта рабочих гипотез;
3. Опишите методы, с помощью которых будет найдено решение уравнений (косвенный МНК, двухшаговый МНК).
Задача №5.
По территориям Сибирского и Уральского федеральных округов России имеются данные о следующих показателях за 2000 год:
Y1 – стоимость валового регионального продукта, млрд. руб.
Y2 - розничный товарооборот, млрд. руб.
X1 – основные фонды в экономике, млрд. руб.
X2 - инвестиции в основной капитал, млрд. руб.
X3- среднедушевые денежные расходы за месяц, тыс. руб.
Изучения связи социально-экономических показателей предполагает проверку следующих рабочих гипотез:
Для их проверки выполнена обработка фактических данных и получена следующая система приведённых уравнений:
Задание:
1. Постройте систему структурных уравнений и проведите её идентификацию;
2. Проанализируйте результаты решения приведённых уравнений;
3. Используя результаты построения приведённых уравнений, рассчитайте параметры структурных уравнений (косвенный МНК); проанализируйте результаты;
4. Укажите, каким образом можно применить полученные результаты для прогнозирования эндогенных переменных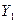 
и 
Задача №6.
Число крестьянских (фермерских) хозяйств (на конец года), -Zt, тыс., в 1993-2000 гг. в Российской Федерации характеризуется следующими сведениями:
| Годы | Zt | Годы | Zt |
| 182,8 | 278,6 | ||
| 270,0 | 274,3 | ||
| 279,2 | 270,2 | ||
| 280,1 | 261,1 | ||
| 278,1 | 261,7 |
Задание:
1. Постройте график фактических уровней динамического ряда -Zt
2. Рассчитайте параметры равносторонней гиперболы: 
3. Оцените полученные результаты:
- с помощью показателей тесноты связи (η и η2 );
- значимость модели тренда (F -критерий);
- качество модели через корректированную среднюю ошибку аппроксимации 
, а также через коэффициент автокорреляции отклонений от тренда - 
4. Выполните прогноз до 2003 года.
5. Проанализируйте полученные результаты.
Задача №7.
Данные о стоимости экспорта (
) и импорта (
) Великобритании, млрд. $, приводятся за период с 1991 по 2000 г.
В уровнях рядов выявлены линейные тренды:
для экспорта -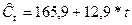 
, а для импорта – 
.
По указанным трендам произведено выравнивание каждого ряда, то есть рассчитаны теоретические значения их уровне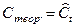й: 
и 
| Годы | Экспорт ()
| Импорт ()
| ||
 .
| 
| 
|
| |
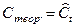
| 185,0 | 178,8 | 209,9 | 197,8 | |
| 190,0 | 191,7 | 221,6 | 213,6 | |
| 180,2 | 204,6 | 205,4 | 229,4 | |
| 204,9 | 217,5 | 227,0 | 245,2 | |
| 242,0 | 230,4 | 263,7 | 261,0 | |
| 260,7 | 243,3 | 286,0 | 276,8 | |
| 281,7 | 256,2 | 306,6 | 292,6 | |
| 271,8 | 269,1 | 314,0 | 308,4 | |
| 268,2 | 282,0 | 318,0 | 324,2 | |
| 281,4 | 294,9 | 334,3 | 340,0 |
Предварительная обработка исходной информации привела к следующим результатам:
| Сt | Qt | t | |
| Ct | 0,9795 | 0,9262 | |
| Qt | 0,9795 | 0,9262 | |
| T | 0,9262 | 0,9262 | |
| Итого | 2365,9 | 2686,5 | |
| Средняя | 236,6 | 268,7 | 5,5 |
| 39,89 | 46,87 | 2,87 |
Задание:
1. Для изучения связи рядов рассчитайте отклонения фактических значений каждого ряда от теоретических (
и 
);
2. Для оценки тесноты связи рассчитайте: 1) линейный коэффициент парной корреляции отклонений от линии тренда: 
; 2) уровней рядов: 
и 3) коэффициент частной корреляции уровней: 
; поясните их значения, укажите причины различий значений парных коэффициентов корреляции (пп. 1 и 2) и схожести коэффициентов парной корреляции отклонений и частной корреляции уровней (пп.1 и 3);
3. Постройте уравнение множественной регрессии с участием временной составляющей:
4. Проанализируйте полученные результаты.
Решение типовых задач
Примечание к решению типовых задач.
При решении типовых задач в табличном процессоре EXCEL и вручную, на калькуляторе из-за особенностей программы при округления цифр промежуточных расчётов некоторые из итоговых результатов могут отличаться. Это не является ошибкой, а лишь особенностью пакетного и ручного решения.
Задача №1.
Приводятся данные за 2000 год по территориям Северо-Западного федерального округа
Таблица №1.
| Территории Северо-Западного федерального округа | Оборот розничной торговли за год, млрд. руб. | Общая сумма доходов населения за год, млрд. руб. |
| А | Y | X |
| 1.Респ. Карелия | 9,4 | 19,1 |
| 2.Респ. Коми | 16,7 | 37,3 |
| 3.Архангельская обл. | 16,3 | 30,0 |
| 4.Вологодская обл. | 12,1 | 27,5 |
| 5.Калининградская обл. | 14,0 | 19,0 |
| 6.Ленинградская обл. | 15,6 | 26,2 |
| 7.Мурманская обл. | 20,5 | 39,5 |
| 8.Новгородская обл. | 9,3 | 14,8 |
| 9.Псковская обл. | 7,3 | 11,6 |
| 10.г.Санкт-Петербург 1) | 83,1 | 133,6 |
| Итого | 121,2 | |
| Средняя | 13,47 | 25,0 |
|
| 4,036 | 9,120 |
| Дисперсия, D | 16,289 | 83,182 |
1) Предварительный анализ исходных данных выявил наличие одной территории (г.Санкт-Петербург) с аномальными значениями признаков. Эта территория исключена из дальнейшего анализа. Значения показателей в итоговых строках приведены без учёта указанной аномальной единицы.
Задание:
1. Расположите территории по возрастанию фактора X. Сформулируйте рабочую гипотезу о возможной связи Y и X.
2. Постройте поле корреляции и сформулируйте гипотезу о возможной форме и направлении связи.
3. Рассчитайте параметры а1 и а0 парной линейной функции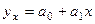 
, степенной 
, линейно-логарифмической функции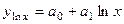 
и параболы второго порядка 
.
4. Оцените тесноту связи с помощью показателей корреляции (r и ρ) и детерминации (r2 и ρ2), проанализируйте их значения.
5. Надёжность уравнений в целом оцените через F-критерий Фишера для уровня значимости a=0,05.
6. На основе оценочных характеристик выберите лучшее уравнение регрессии.
7. По лучшему уравнению регрессии рассчитайте теоретические значения результата (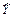
), по ним постройте теоретическую линию регрессии и определите скорректированную среднюю ошибку аппроксимации - ε'ср ., оцените её величину.
8. Рассчитайте прогнозное значение результата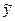 
, если прогнозное значение фактора (
) составит 1,062 от среднего уровня (
).
9. Рассчитайте интегральную и предельную ошибки прогноза (для a=0,05), определите доверительный интервал прогноза (; ), а также диапазон верхней и нижней границ доверительного интервала (), оценивая точность выполненного прогноза.
Решение:
1.Для построения графика расположим территории по возрастанию значений фактора 
. См. табл. 2. Если график строится в табличном процессоре EXCEL, то в исходной таблице фактор должен находиться на первом месте, а результат – на втором. Из графика может быть сделан вывод о возможной форме связи оборота розничной торговли (Y) с общей суммой доходов населения (X). В этом случае для описания зависимости следует построить несколько моделей разного вида и на основе оценочных характеристик выбрать оптимальную форму модели.
Таблица №2.
| Территории Северо-Западного федерального округа | Общая сумма доходов населения за год, млрд. руб. | Оборот розничной торговли за год, млрд. руб. |
| А |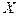 
| 
|
| 1.Псковская обл. | 11,6 | 7,3 |
| 2.Новгородская обл. | 14,8 | 9,3 |
| 3.Калининградская обл. | 19,0 | 14,0 |
| 4.Респ. Карелия | 19,1 | 9,4 |
| 5.Ленинградская обл. | 26,2 | 15,6 |
| 6.Вологодская обл. | 27,5 | 12,1 |
| 7.Архангельская обл. | 30,0 | 16,3 |
| 8.Респ. Коми | 37,3 | 16,7 |
| 9.Мурманская обл. | 39,5 | 20,5 |
| Итого | 121,2 | |
| Средняя | 25,0 | 13,47 |
|
| 9,120 | 4,036 |
| Дисперсия, D | 83,182 | 16,289 |
2. Обычно моделирование начинается в построения уравнения прямой: 
, отражающей линейную форму зависимости результата Y от фактора X.
3. Расчёт неизвестных параметров уравнения выполним методом наименьших квадратов (МНК), построив систему нормальных уравнений и решая её, оносительно неизвестных а0 и а1. Для расчёта используем значения определителей второго порядка Δ, Δа0 и Δа1 Расчётные процедуры представим в разработочной таблице, в которую, кроме значений Y и X, войдут X2, X*Y, а также их итоговые значения, средние, сигмы и дисперсии для Y и X. См. табл.3.
Расчётная таблица №3
| № |
|
| 
| 
| 
| 
| 
| 
|
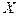
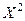
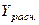
| А | ||||||||
| 11,6 | 7,3 | 134,6 | 84,7 | 8,1 | -0,8 | 0,6 | 5,2 | |
| 14,8 | 9,3 | 219,0 | 137,6 | 9,4 | -0,1 | 0,0 | 0,4 | |
| 19,0 | 14,0 | 361,0 | 266,0 | 11,1 | 2,9 | 8,4 | 19,5 | |
| 19,1 | 9,4 | 364,8 | 179,5 | 11,1 | -1,7 | 2,9 | 11,2 | |
| 26,2 | 15,6 | 686,4 | 408,7 | 13,9 | 1,7 | 2,9 | 10,9 | |
| 27,5 | 12,1 | 756,3 | 332,8 | 14,5 | -2,4 | 5,7 | 15,7 | |
| 30,0 | 16,3 | 900,0 | 489,0 | 15,5 | 0,8 | 0,6 | 5,5 | |
| 37,3 | 16,7 | 1391,3 | 622,9 | 18,4 | -1,7 | 2,9 | 11,3 | |
| 39,5 | 20,5 | 1560,3 | 809,8 | 19,3 | 1,2 | 1,4 | 8,0 | |
| Итого | 225,0 | 121,2 | 6373,6 | 3331,0 | 121,2 | 0,0 | 25,4 | 98,4 |
| Средняя | 25,0 | 13,5 | — | — | — | — | — | 10,9 |
| Сигма | 9,12 | 4,04 | — | — | — | — | — | — |
| Дисперсия, D | 83,18 | 16,29 | — | — | — | — | — | — |
| Δ= | 6737,76 | — | — | — | — | — | — | — |
| Δа0= | 23012,4 | 
| 3,415 | — | — | — | — | — |
| Δа1= | 2708,91 | 
| 0,402 | — | — | — | — | — |
3. Расчёт определителя системы выполним по формуле:
9*6373,6 – 225,0*225,0 = 6737,76;
Расчёт определителя свободного члена уравнения выполним по формуле:
121,2*6373,6 – 3331,0*225,0 = 23012,4.
Расчёт определителя коэффициента регрессии выполним по формуле:
9*3331,0 – 121,2*225,0 = 2708,91.
4.Расчёт параметров уравнения регрессии даёт следующие результаты:
; 
.
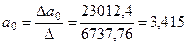В конечном счёте, 
получаем теоретическое уравнение регрессии следующего вида:
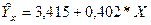
В уравнении коэффициент регрессии а0 = 0,415 означает, что при увеличении доходов населения на 1 тыс. руб. (от своей средней) объём розничного товарооборота возрастёт на 0,415 млрд. руб. (от своей средней).
Свободный член уравнения а0 =3,415 оценивает влияние прочих факторов, оказывающих воздействие на объём розничного товарооборота.
5.Относительную оценку силы связи даёт общий (средний) коэффициент эластичности:
В нашем случае, когда рассматривается линейная зависимость, расчётная формула преобразуется к виду:
Это означает, что при изменении общей суммы доходов населения на 1% от своей средней оборот розничной торговли увеличивается на 0,744 процента от своей средней.
6. Для оценки тесноты связи рассчитаем линейный коэффициент парной корреляции:
