ПОЛНОТА СИСТЕМЫ ФУНКЦИЙ АЛГЕБРЫ Л0ГИКИ

ОСНОВНЫЕ ПОНЯТИИ

Развитие вычислительной техники потребовало разработки специфического математического аппарата, основой которого стали фундаментальные понятия математической логики. Дискретность процессов арифметических вычислений и логических выводов требовала создания специальных физических устройств, реализующих эти процессы, причем с максимально возможной скоростью, что, в свою очередь, стимулировало разработку математических моделей дискретных процессов, которые в наиболее общей форме реализовались в новом разделе математики - дискретной математике, построенной на основных понятиях математической логики.

Известно, что если некоторая величина задана в какой-либо системе счисления, например в десятичной, то ее всегда можно перевести в двоичную систему, использующую для записи всего два знака, например 0 и I. Двоичный код удобен тем, что большинство физических приборов, реализующих те или иные автоматы, имеют два состояния - активное и пассивное. В связи с этим будем рассматривать функции от любого конечного числа переменных , каждая из которых, а также каждый аргумент которых принимают лишь два значения 0 и I. Независимые переменные этих функций, называемые пропозициональными переменными, будем обозначать не только через , но и любыми строчными буквами латинского алфавита. В математической логике (в алгебре логики) 0 идентифицируется с ложным суждением, а I - с истинным.

Если - некоторое суждение, то посредством обозначим его отрицание. Формула , читаемая "х и х₂ ", выражает логическое умножение, которое будет являться истинным тогда и только тогда, когда истинно каждое из суждений и . Логическое умножение называют конъюнкцией. Через обозначают логическое сложение, называемое дизъюнкцией и читаемое как " или ". Дизъюнкция истинна, если истинно хотя бы одно из составляющих ее суждений или .

Выражение "из следует ", обозначаемое , называют импликацией. Условились считать, что импликация ложна лишь в том случае, когда суждение истинно, а ложно.

Нетрудно убедиться, что импликация эквивалентна .

Говорят, что суждения и эквивалентны (и обозначают это по­средством ), если оба суждения и одновременно истинны или ложны.

Истинность или ложность перечисленных выше элементарных операций над суждениями отражены в табл. I.

 

Таблица I

				I	I	I
	I		I	I		I
I			I
I	I	I	I	I	I	I

Из простых суждений с помощью введенных операций "и", "или" и "не", а также импликации и эквиваленции можно составлять слож­ные суждения. Правила подобных построений составляют раздел ал­гебры логики. Прежде чем переходить к операциям алгебры логики, введем понятие функции алгебры логики.

Функцией алгебры логики назовем любую функцию , принимающую лишь значения 0 и I и определенную на множестве переменных 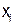, принимающих также только значение 0 и I. Функ­ция f будет определена, если заданы ее значения при всех значе­ниях ее аргументов . Поскольку число всех возможных наборов двоичных переменных 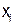равно 2, то число всех возмож­ных функций алгебры логики, зависящих от n переменных 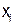, равно

Это число очень быстро возрастает с ростом n, и поэто­му задавать такие функции в виде нижеследующих таблиц при n> 5 становится практически невозможным; в этом случае их задают не таблицами, а формулами. Табличное представление функции чаще всего дается в форме табл. 2.

Таблица 2

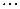
0 0	0 0	f (0,...,0)
I I	I 0	f (I,...,I,0)
I I	I I	f (I,...,I)

Множество всех функций алгебры логики обычно обозначают че­рез .

Переменная 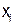называется существенной, а функция - существенно зависящей от этой переменной, если найдется такой набор значений переменных (),что имеет место не­равенство . В противном случае переменная 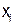называется несущест­венной, или фиктивной. Две функции равны, если они отличаются друг от друга на фиктивную переменную. Существует два вида функ­ций, не содержащих существенных переменных - это функции, тож­дественно равные 0 или I.

По определению пропозициональные переменные и константы 0 и I называются формулами. Формулами считаются также любые выра­жения, составленные из формул c применением операций конъюнк­ции, дизъюнкции, импликации, эквиваленции и отрицания.

Каждая формула определяет некоторую функцию алгебры логики, причем различным формулам может отвечать одна и та же функция. Например, формуле, задающей импликацию , отвечает та же функция , что и формуле .В качестве другого примера рассмотрим, например, формулу , определяющую сложение по модулю 2. То, что это сложение определяет формулу алгебры логики, следует из равенства (табл. 3).

Таблица 3

 

	I	I	I
I		I	I
I	I

 

Нетрудно убедиться также, что формулы и -задают одну и ту же функцию алгебры логики, так же как одну и ту же функцию задают и формулы и . Чтобы убедиться в этом, достаточно построить таблицу значений функций, определенных этими формулами.

В дальнейшем формулы, отличные от пропозициональных пере­менных, будем обозначать большими буквами и использовать в фор­мулах по возможности меньше скобок, условившись, что знаки конъюнкции и дизъюнкции определяют более тесную связь, чем зна­ки импликации и эквиваленщи, а знак конъюнкции задает более сильную связь, чем знак дизъюнкции. При подобных предположениях в отношении обозначений можно существенно уменьшить число ско­бок в формулах, например, формулу

можно переписать в виде

Операции конъюнкции, дизъюнкции, эквиваленции и отрицания обладают рядом свойств, позволяющих существенно упрощать формулы алгебры логики.

 

 

1. Операции конъюнкции и дизъюнкции обладают следующими свойствами, очень сходными c аналогичными свойствами в теории множеств, если операции конъюнкции сопоставить операцию пересе­чения множеств, а операции дизъюнкции - операцию объединения

множеств:

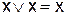, (закон идемпотентности);

, , ,

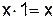2. Следующие три закона отражают естественные отношения в логике высказываний:

(одновременно и то, и ему противоположное невозможно);

(т.е. это или ему противоположное достоверно);

(двойное отрицание есть утверждение).

1. Закон ассоциативности конъюнкции, дизъюнкции и эквиваленции:

что позволяет вообще отказаться от скобок, когда одна и та же операция повторяется последовательно более одного раза. 6

4. Операции конъюнкции, дизъюнкции и эквиваленции облада­ют также свойством коммутативности:

1. Операции конъюнкции и дизъюнкции обладают свойством дистрибутивности (распределительности) относительно друг друга:

Используя сформулированные свойства, можно упрощать слож­ные формулы, приводя их к элементарным, называемым тупиковыми, не допускающим дальнейшего упрощения.

Обратимся к выводу общих формул представления функций ал­гебры логики.

Покажем, что любая функция алгебры логики может быть вы­ражена через конъюнкцию, дизъюнкцию и отрицание.

Теорема I. Любая функция алгебры логики допускает разло­жение по любому числу К переменных из множества n всех пере­менных:

 

где

Доказательство. Как следует, из обозначений теоремы, 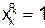в том и только том случае, если . Для проверки теоремы достаточно подставить в функцию f и ее разложе­ние произвольное множество допустимых значений

и учесть указанное свойство 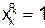при и 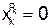в ином случае:

Следствие. Любая функция алгебры логики () может быть выражена через конъюнкцию, дизъюнкцию и отрицание:

где логическое суммирование проводится только по тем комбинаци­ям 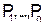), для которых f = I. Это разложение функции алгебры логики называют совершенной дизъюнктивной нормальной формой.

 

Разложим, например, функцию f (, приведя ее к совершенной дизъюнктивной нормальной форме: .

Если все значения функции заданы, то, подставляя их в эту формулу, полу­чаем окончательный вид разложения. Например, пусть функция f задана своими значениями: .

Тогда .

Любая функция алгебры логики, исключая тождественно равную нулю, может быть представлена в совершенной дизъюнктивной нор­мальной форме (СДНФ), составленной из произведений (), соединенных операцией . Можно, однако, показать, что функция алгебры логики могут быть также представлены в виде произведения членов вида (). Подобное представление называется совершенной конъюнктивной нормальной фор­мой (СКНФ). Для нахождения связи между двумя этими представле­ниями полезно предварительно ввести понятие двойственной функ­ции: функция называется двойственной к функции

Очевидно, , а следовательно, двойственная функция получается из таблицы значений исходной функция в результате взаимной замены 0 и I и переворачивания столбца значе­ний функции (табл. 4).

Таблица 4

		I	I
	I	I	I
I
I	I

 

Из определения двойственной функции следует, что 0 и I двойственны друг другу, функции и двойственны самим себе, повторное применение операции двойственности возвращает к ис­ходной функции, т.е. .

Следующая теорема позволяет по заданной формуле А, опре­деляющей функцию , построить формулу В, определяющую двойственную функцию .

Теорема 2. Пусть - некоторая функция алгебры логики, представляющая собой суперпо­зицию более простых функций алгебры логики , i-я из которых зависит от произвольного числа переменных /из множества /, обобщенно обозначенного через .

Тогда

Доказательство:

Следствие. Если формула A() определяет функцию. , то формула определяет двойственную функцию . Нетрудно проверить, что функции взаимно двойственны друг другу. Отсюда следует, что для получения фор­мулы , двойственной к , следует взаимно поменять 0 и I и дизъюнкцию и конъюнкцию, например:

 

Из определения двойственной функции следует, что , а отсюда, в свою очередь, следует правило де Моргана: чтобы получить отрицание некоторой формулы, следует образовать двойственную формулу и заменить в ней аргументы их отрицаниями, или, в другой формулировке, отрицание всякой фор­мулы, выраженной через отрицание, дизъюнкцию в конъюнкцию, мо­жет быть получено заменой аргументов их отрицаниями и взаимной заменой операций дизъюнкции и конъюнкции.

 

Примеры: I) , ;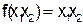

2) , .

Покажем теперь, что любую функцию алгебры логики можно представить в виде СКНФ. Пусть , а следовательно, .

Разложим в СДНФ:

Применяя правило де Моргана и обозначая через П произведение (конъюнкцию), получаем

.

Из сравнения представлений функции алгебры логики в виде СДНФ и в виде CKНФ следует правило перехода от СДНФ к СКНФ: необходимо образовать логическую сумму дизъюнктивных членов, не входящих в СДНФ, поменять местами операции дизъюнкции и конъюнкции и заменить аргументы их отрицаниями.

При операциях c формулами алгебры логики полезными оказы­ваются следующие правила:

I. Логическое произведение двух разных дизъюнктивных чле­нов вида () равно нулю. Это следует из того, что в разных дизъюнктивных членах найдется по крайней мере одна та­кая переменная , что в один из членов она входит в вида , а в другой - в виде , а следовательно, с учетом свойства коммутативности конъюнкции произведение можно будет представить в виде )(•), где первый сомножитель равен нулю.

 

2. Логическая сумма двух разных конъюнктивных членов вида

)() равна единице. Это следует из того, что подобную сумму можно представить в вида (,где пер­вая сумма равна единице, а следовательно, равна единице и всясумма. 3. Логическая сумма всех попарно различных дизъюнктивных членов равна единице. Это следует из теоремы представления произвольной функции алгебры логики в ви­де СДНФ и из того, что если в данном представлении фигурируют вcе дизъюнктивных членов, то это означает, что функция тож­дественно равна единице.

4. Логическое произведение всех попарно различныхконъюнктивных членов

равно нулю, что следует из теоремы о представлении произвольной функции f в ви­де СКНФ и из того, что если в этом представлении присутствуют все конъюнктивные члены (а в произведении участвуют только чле­ны, для которых ), то .

 

ПОЛНОТА СИСТЕМЫФУНКЦИЙ АЛГЕБРЫЛ0ГИКИ

Выше было показано, что любая функция алгебры логики может быть выражена через конъюнкцию, дизъюнкцию и отрицание, т.е. через функции . Можно поставить вопрос: существуют ли еще какие-либо системы функций, через которые можно выразить любую функцию из класса всех булевых функций? Как увидим, ответ на этот вопрос положительный. Более того, най­дены даже необходимые и достаточные условия того, чтобы задан­ная система функций обладала подобным свойством (полноты).

Система функций { } называется полной, если любую функ­цию из множества всех булевых функций можно задать в виде некоторой формулы от функций этой системы.

Примеры. Полными будут системы всего из двух функций поскольку посредством операции от­рицания первая из них может быть дополнена конъюнкцией

линейных функций,

а вторая - дизъюнкцией

что приводит к системе функций полнота которой уже была

установлена ранее. Более того, можно показать, что всего одна функция ,

по определение равная функцииc и называемая функцией Шеффера, образует полную систему. Функция Шеф-фера равна нулю (т.е. ложному суждению), только когда равны единице (т.е. когда истинны) и . Составляя таблицу этой функции, легко видеть, что отрицание может быть получено, ес­ли в этой функции берутся одинаковые аргументы , а дизъюнкция равна ,что следует из определения отрицания и определения самой функции Шеффера (табл. 5).

Таблица 5

		I
	I	I	I
I		I	I
I	I		I

 

Существует множество других наборов полных функций. Оце­нить полноту произвольного набора функций посредством эквива­лентных преобразований этих функций в функции какого-либо из известных наборов полных функций бывает не всегда просто и удобно. Ниже будет определено пять классов функций, опираясь на которые можно сформулировать критерий полноты системы функ­ций. Но прежде чем переходить к рассмотрению этих пяти классов, укажем на полезное свойство замкнутости класса функций.

Если М - подмножество функций из , то замыканием М в , обозначаемым [ М], называется множество всех тех функ­ций из , которые могут быть выражены в виде формул через функции из множества М. Класс функций называется замкнутым, если он совпадает со своим замыканием. Например, класс L всех линейных функций

замкнут, поскольку любая функция из , определяемая как неко­торая линейная комбинация, принадлежит этому классу.

Класс L будет играть роль одного из пятb классов функций, через которые выражается критерий полноты системы функций.

Заметим, что если H - некоторая система функций и если , * то H - полная система функций.

Вторым классом функций, важным для оценки полноты системы функций, является класс всех булевых функций , сохраняющих 0, т.е. таких, которые удовлетворяют условию

.

функциями из класса являются, например, следующие:

,

а также любые однородные линейные функции. Не принадлежат этому классу, например, .

Класс замкнут, поскольку если функции f, принадлежат классу , то и функция

принадлежит этому классу. В самом деле, имеем

Третьим классом является класс всех функций алгебры ло­гики, сохраняющих единицу, т.е. удовлетворяющих условию

.

В этот класс входят, например, функции , но не входят функции . Поскольку класс является двой­ственным классу , то он тоже замкнут, как и .

К четвертому классу относится класc S так называемых само­двойственных функций, т.е. таких, что f *= f, называемых также "нечетными": поскольку , что как раз и выражает свойство нечетности. Самодвойственной является, на­пример, функция , так как , а также функция x.

Замкнутость класса S следует из того, что если , то и .

В самом деле, имеем (согласно теорема о двойственной функции):

Пятый класс функций образует класс М монотонных функций, т.е. функций, удовлетворяющих следующему условию:

если . Нетрудно проверить, что монотонными являются функции 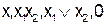и I. Примем без доказательства, что класс монотонных функций замкнут.

Основываясь на пяти построенных классах функций, можно сформулировать теорему о функциональной полноте системы функций алгебры логики.

Теорема. 3 (о полноте). Чтобы система функций { } была полной необходимо и доста­точно, чтобы она не содержалась целиком в одном из пяти классов .

Эта теорема позволяет проверить, является некоторая вы­бранная система функций полной или нет. Понятно, что система заведомо неполна, если все функции этой системы принадлежат не­которому классу , поскольку в этой системе нет функции, не принадлежащей классу . В то же время система функций не окажется полной, если в ней не будет функции, кото­рая не является функцией класса , где под понимается лю­бой из пята классов .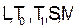

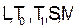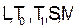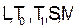В ряда случаев удобнее вместо пяти классов говорить о пяти свойствах . В подобной трактовке можно сказать, что система функций не будет полной, если в ней не найдется функции, не обладающей свойством ( - любое из свойств ). Например, система функций () и ) не является полной, так как обе эти функции удовлет­ворят свойству и в этой системе нет функции, не удовлетво­ряющей давнему свойству. Если же к этой системе добавить, на­пример,I то система станет полной, так как 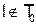. Можно про­верить и убедиться, что функция Шеффера не обладает ни одним из пяти свойств, а следовательно, она образует полную систему. В общем случае доказано, что из всякой полной системы можно вы­делить полную подсистему, содержащую не более четырех функций.

Легко проверить, что система функций полна: так как обладает свойствами не обладает свойствами L и S, то вся система не обладает всеми пятью свой­ствами, т.е. не содержится ни в одном из пяти классов.