ПРИМЕР ФИЗИЧЕСКОЙ РЕАЛИЗАЦИИ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ

Рассмотрим некоторые простейшие реализации введенных выше элементарных функций алгебры логики ва примерах простых радио­электронных устройств. В таких устройствах можно принять, что высокое напряжение соответствует числу I в алгебре логики, а низкое - числу 0. В подобной интерпретации однокаскадный тран­зисторный усилитель можно рассматривать в качестве прибора, реализующего функцию отрицания. Действительно, рассмотрим уси­лительный каскад на одном транзисторе в схеме о общим эмитте­ром (например, с транзистором структуры n-р-n). В отсутст­вие сигнала на базе транзистора (т.е. при ) транзиcтop не проводит и на его выхо­де имеется максимально возможное напряжение которое обозначим через I (рис. I).

Рис. I

При подаче на вход положительного напряжения, которое обо­значим через , транзистор открывается, на его выходе напряжение становится очень малым и его можно считать (по срав­нению с напряжением закрытого транзистора) приближенно равным нулю: . Отсюда следует, что транзистор реализует

функцию . Можно сказать также, что оператор транзистора .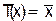

Если же усилительный каскад построен по схеме с общим кол­лектором, т.е. является эмиттерным повторителем, то он выдает на выходе напряжение той же фазы и почти той же амплитуда, что и на входе. Таким образом, катодный повторитель реализует функ­цию , т.е. оператор катодного повторителя К(х) = х, (рис. 2).

Если же объединить эмиттеры двух катодных повторителей и подавать сигналы на их базы одновременно или порознь, то не­трудно убедиться, что подобный каскад реализует функцию .

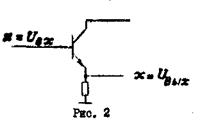
Рис. 2

В самом деле, напряжение на выхода будет отсутствовать только тогда, когда оно будет от­сутствовать одновременно на обеих базах транзисто­ров; это как раз и означает реализацию операции дизъ­юнкции (рис. 3). •

Рис. 3

Таким образом, двойной эмиттерный повторитель совместно с усилительным каскадом с общим эмиттером представляет собой фи­зическую систему, реализующую полную систему функций алгебры логики, т.е. функции и .

Дизъюнкцию можно реализовать также с помощью диодов и других более сложных схем (рис. 4).

Функцию Шеффера, обра­зующую полную систему функ­ций, можно получить с помощью схемы, составленной из двух последовательно включенных транзисторов, работающих на общую нагруз­ку (рис. 6). Действительно, в этом случае сигнал на выходе схемы будет максималь-

Рис. 4 ным (равным единице) в той случае, если отсутствует сигнал (положи­тельный) хотя бы на одной из баз транзистора. И только в случае, когда на обеих базах сигнал поло­жительный, на выходе сигнал будет минимальным (поскольку транзисторы проводят сразу оба), т.е. равным 0. Если теперь сигнал в виде функции Шеффера подать на усилительный каскад с общим эмиттером, то на выходе получится сигнал, равный отрицанию функции Шеффера (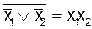), что равно конъюнкции.

Нетрудно убедиться, что если два транзистора работают на общую нагрузку в схеме с общим эмиттером, то реализуется функция , Дей­ствительно, когда открыт один тран­зистор (на входе I), то на выходе 0. Если же они закрыты оба, т.е.

, то на выходе напряжение максимально (т.е. равно I), а подоб­ная функция алгебры логики как раз и определяет 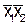(рис, в).

Риc. 5

Рис. 6