УПРОЩЕНИЕ ЛОГИЧЕСКИХ ФОРМУЛ

Известно несколько методов упрощения формул алгебры логи­ки. Однако эти методы весьма трудоемка, когда число переменных велико. При минимизации дизъюнктивных нормальных форм обычно используют операцию поглощения , где под функцией f понимается произвольная элементарная дизъюнкция или конъюнкция. Это свойство является очевидным следствием свойства дистрибутивности дизъюнкции. При преобразованиях коньюнктивных нормаль­ных форм используется аналогичное свойство , вытекающее из свойств дистрибутивности, например из отношений

На практике часто применяют также операции склеивания и ,

получающиеся из формулы

Упрощение формул с помощью операций алгебры логики, как уже говорилось, весьма трудоемко. Если число переменных в функ­ции 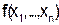не более пяти, удобным оказывается метод не­определенных коэффициентов, который применим как при аналити­ческом задании функции с помощью формулы, так и при задании ее с помощью таблицы значений. Пусть, например, значения функции заданы в виде таблицы. Напишем общее разложение этой функции:

При имеем

При

При

При

Подставляя значения функции из таблицы, получим все неиз­вестные коэффициенты. Поскольку число коэффициентов больше числа уравнений, то часть коэффициентов можно положить равными нулю. Обычно нулю полагают наиболее сложные коэффициенты. Рас­смотрим процедуру нахождения аналитического минимального вида функции на примере.

Пример. Пусть f(0,0)=0, f(0,l) = 0, f(l,0)=0, f(1,1)=1. Подставляя эти значения в уравнения для определения коэффициентов, получаем .

Отсюда следует: . Таким образом,

функция алгебры логики имеет вид

Если функция зависит от трех и более перемен­ных, то задавать таблицу ее значений в том виде, как мы это делай раньше, представляется слишком громоздким. В этом слу­чае переменные разделяют на две группы и задают такую функцию в форме табл. 6 для случая, когда число аргументов равно трем.

Таблица 6

Переменные
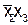
	I	I
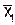
	I			I

Иногда значения функции бывают заданы не для всех наборов переменных . Это означает, что подобная функция не всюду определена. Однако формула алгебры логики всегда задает функ­цию, определенную всюду. Поэтому подобную функцию следует до­определить. Доопределение значений функции может проводиться произвольно, но лучше доопределять ее так, чтобы задающая ее аналитическая формула оказалась как южно более простой.

ПРЕДИКАТЫИ КВАНТОНЫ

Изложенные выше операции алгебры логики можно применять и к двоичным переменным, зависящим от переменных, принимающих значения из некоторого (не обязательно конечного) множества м. Такие функции называют предикатами в предметной области М. С помощью операций коньюнкции, дизъюнкции и отрицания можно записывать многие высказывания. К сожалению, этих операций не­достаточно для выражения более сложных высказываний. Например, невозможно на изложенном математическом языке выразить фразу: "для любого >0 найдется > 0, такое, что как только ". Легко видеть, что для запи­си этой фразы в виде формулы необходимо еще формализовать на математическом языке (языке алгебры логики) понятая "существо­вания" и "общности". Операции существования и общности, вводи­мые в математической логике (в логике предикатов), изображают­ся кванторами существования и общности. С их помощью рассмат­ривавшийся выше язык исчисления высказываний расширяется до так называемого языка исчисления предикатов.

В математической логике запись f (х) = I означает, что суждение х обладает свойством f истинно. Предикат f(x), зависящий от одной переменной, называется одноместным предика­том, а если независимых переменных несколько, то - многоместным предикатом. Квантор существования обозначают обычно посред­ством , а квантор общности . Запись () f(x) означает, что существует такое х, для которого выполняется свойство f, Если, например, /(х)- предикат, означающий, что "x четно", то суждение ()f(x) будет истинным, если под х понимается, например, множество натуральных чисел, а суждение ( x)f(x) будет ложным, так как не все натуральные числа четны.

Квантор общности можно считать обобщением конъюнкция. В самом доле, если, например, 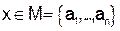, то запись

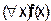эквивалентна конъюнкция ,

а запись f(x) эквивалентна дизъюнкции .

В формулах предметная переменная, относящаяся к квантору, называется связанной переменной; например, в записи переменная является связанной, а перемен­ная свободна. По аналогии, например, с переменной интегриро­вания связанную переменную можно обозначать любой буквой, переименовывая её в формулах произвольным образом.

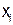Формула может включать несколько предикатов и несколько свободных переменных, например , где А, В,С,... - предикаты, а - свободные переменные. Если предикаты в этой формуле рассматривать в качестве переменных, то формула будет определять некоторый оператор T, отображающий пространство переменных предиката А,В,С... d n-мерный переменный предикат .

В логике исчисления предикатов не всякую формулу можно считать за формулу исчисления предикатов, а только такую, которая определяет осмысленную выражение. Кроме того, даже а осмысленных выражениях не допускается использование одной и той же переменной в качестве связанной и свободной. Формулы исчисления предикатов должны удовлетворить следующим условиям,

1. Всякий предикатный символ А(), рассматриваемый как функция от некоторых предметных переменных, считается формулой, а все предметные переменные этого предиката являются свободными переменными; формулами считаются также I (истина) и 0 (ложь).

2. Если Ф(,А,В,С,...)- формула исчисления высказываний, где А,В, С,.,, - двоичные переменные, то она останется формулой при замене A,B,C,.,, на любые формулы если лю­бая свободная переменная в любой из формул 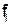не будет входить

в качестве связанной переменной ни в одну из других формул; каковы были переменные (предметные) в формулах 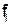, т.е. сво­бодными или связанными, такими они должны остаться и в сложной формуле Ф().

3. Если А(... 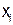...)- формула, в которой 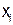- свободная переменная, то выражения и также являются формулами, в которых переменная 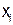оказывается связанной, а остальные переменные остаются такими же, какими они были в исходной формуле А.

Все формулы в логике предикатов должны удовлетворять пере­численным требованиям. Если в п. 3 формула А(.... ...) содер­жит какие-либо кванторы, то они считаются подчинёнными квантору() или , примененному к формуле А,

В общем случае квантор имеет единичный ранг, если ему не подчинены никакие другие кванторы, Квантор имеет ранг K+1, если в формуле, на которую он действует, есть хотя бы один квантор ранга К и нет кванторов большего ранга. Внешний квантор формулы всегда имеет наивысший ранг. Наивысший ранг формулы называется кванторной глубиной формулы.

Формулы исчисления предикатов, как включающие, так и не включающие кванторы, допускают многие из тех тождественных преобрааований, которые рассматривались выше. Тождественные преоб­разования формул, включающих кванторы, должны проводиться с уче­том специфики последних. Определенную помощь здесь оказывает тот факт, что между квантором общности и конъюнкцией, с одной стороны, и квантором существования и дизъюнкцией, о другой сто­роны, существует тесная связь, отмеченная выше.

Формулы алгебры логик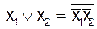и и , определяющие эквивалентности, вытекающие из правила де Моргана, переносятся и на формулы исчисления предикатов, включающие кванторы; при этом отрицание квантора общности заменяется квантором существования, и наоборот, например: ()

;здесь квантор существует неявно предполагает выполнение операции дизъюнкции, а квантор общности -операция конъюнкции. Приведенные тождества называются эквивалентностями с отрицаниями.

Аналогами свойств дистрибутивности конъюнкции и дизъюнкции относительно друг

друга служат следующие эквивалентности для предикатов:

.

Однако полностью свойства дистрибутивности и перестановоч­ности операций, имеющие место в алгебре логики, не сохранятся для предикатов. Аналогом вышеприведенной формулы эквивалентно­сти для квантора существования, примененного к дизъюнкции, слу­жит эквивалентность для квантора общности, примененного к коньюнкции

а аналогом перестановочности кванторов существования служит перестановочность кванторов общности

;

в то же время левые и правые части следующих отношений не явля­ются эквивалентными друг другу:

Заметим, что если в этих высказываниях справедливы левые части, то нельзя утверждать, что и правые будут справедливы; однако если истинны правые части, то истинными будут и левые. Напри­мер, в отношении всех вещественных чисел можно сказать: , и это высказывание, очевидно, истинно; в то же время высказывание явно ложно

Из сравнения приведенных отношений можно заключить, что если в формуле имеется несколько кванторов существования и от­сутствуют кванторы общности, то кванторы существования могут рассматриваться в любой последовательности. Это справедливо и в отношении кванторов общности в отсутствие в той же формуле кванторов существования. Однако если в формуле стоят одновре­менно кванторы существования и общности, то перестановка этих кванторов меняет смысл формулы. Наконец, можно заключить, что квантор существования дистрибутивен относительно дизъюнкции (а следовательно, может выноситься за скобки), что является следствием того, что этот квантор является по существу аналогом операции дизъюнкции. Точно так же квантор общности, являющийся аналогом конъюнкции, дистрибутивен относительно конъюнкции, т.е. может выноситься за скобки, когда применяется к предика­там, связанным операцией конъюнкции.

Подобно тому, как в математическом анализе постоянный множитель может быть вынесен за знак интегрирования или диффе­ренцирования, в логике предикатов можно выносить из-под знака квантора ту часть формулы, которая не зависит от предметной переменной (x), с которой связан квантор, например: . Легко записать и остальные три случая выноса постоянной из-под знака квантора:

Всюду в приведенных выше формулах своего рода "независимой переменной" кванторов у нас служили предметные переменные х, у,.... Однако еще большая формализация языка достигается, если в качестве "независимых переменных" кванторов рассматри­вать не только предметные переменные, но и предикатные перемен­ные, или же независимыми переменными считать только предикатные переменные. Например, если А(х)- одноместный предикат, а х -предметная переменная, то высказывание выражает тот факт, что утверждение справедливо для любого од­номестного предиката при всех значениях переменной х, являю­щейся в данном случае свободной. Очевидно, приведенное высказы­вание ложно при любых х. Рассмотренные выше эквивалентности для предикатов распространяются и на случай, когда квантор дей­ствует не на предметную, а на предикатную переменную.

Для многих приложений в качестве предметных переменных X, у,... целесообразно рассматривать натуральный ряд чисел, ко­торый можно интерпретировать так же, как дискретные значения времени. Подобная интерпретация делает естественный введение понятия ограниченного кванторе, например ограниченного квантора существования и ограниченного квантора общности .

Скажем, выражение означает существование t из интервала (), для которого удовлетворяется требование X(t). Приведенное высказывание о использованием понятия ограниченного квантора можно выразить, однако, и с по­мощью обычного квантора (без ограничений): . Иными словами, понятие ограниченного квантора не вносит ничего нового в логику высказываний, а всего лишь упрощает обозначе­ния.

Установленные выше эквивалентности для кванторов имеют место и для ограниченных кванторов, за исключением лишь свойст­ва коммутативности кванторов, что означает недопустимость изме­нения порядка применения ограниченных кванторов. В самой деле, например,

поскольку в правой части этого неравенства переменная t оказыва­ется одновременно и свободной, и связанной, что недопустимо по определению формул алгебры логики.

Все формулы, выводимые в исчислении предикатов, выражают тождественно истинные высказывания, и любая тождественно истин­ная формула выводила в исчислении предикатов. Отсюда следует, что в исчислении предикатов невыводимы какие-либо действительно содержательные высказывания, например математические теоремы. Но если к аксиомам исчисления предикатов добавить какие-либо невыводимые в этом исчислении формулы, то можно надеяться выве­сти и еще какие-то формулы и получить нетривиальные результаты. Подобный подход позволяет рассматривать с позиций математичес­кой логики такие дисциплины, как арифметика, геометрия, теория множеств. Однако при этом необходимо исследовать вопрос о внут­ренней непротиворечивости рассматриваемых аксиом.

Исчисление высказываний называют непротиворечивым, если в нем нельзя вывести никакую пару формул, отрицающих друг дру­га. Исчисление называется противоречивым, если в нем можно од­новременно вывести пару формул А и . В противоречивой системе можно вывести все формулы, а значит, в такой системе неразличимы истина и ложь.

Следовательно, чтобы утверждать о непротиворечивости си­стемы, достаточно показать, что в этой системе существует хотя бы одна формула, которую нельзя вывести. Для доказательст­ва непротиворечивости какой-либо системы исчисления необходимо привлечь некие факты, не следующие из аксиом этой системы. Понятно, что эти факты должны браться из источника, в отношения непротиворечивости которого у нас не имеется сомнений. В на­стоящее время в качестве такого источника используют теории множеств, рассматривая ее как наиболее общий источник предпосы­лок для доказательства более частных систем исчисления. Однако и сама теория множеств нуждается в доказательстве непротиворе­чивости, что, правда, уже выходит за возможности современной математики.

Пользуясь тем, что для доказательства непротиворечивости системы исчисления достаточно показать существование какой-либо формулы, которую нельзя вывести из этой системы, можно доказать, например, непротиворечивость ограниченной ариф­метики, получающейся, если из исходных понятий аксиоматической арифметики устранить аксиому полной математической индукции. Для доказательства непротиворечивости ограниченной арифметики достаточно показать, что в ней невыводима формула " ".