ДЕТЕРМИНИРОВАННЫЕ ОПЕРАТОРЫ И СЕТИ

Рассмотрим некоторые приложения аппарата математической логики к проектированию и исследованию работы автоматических устройств, связанных с переработкой дискретной информации. Пусть автомат имеет m входов и n выходов , каждый из которых может принимать конечное число различных со­стояний. Например, пусть вход может иметь лишь два состоя­ния, а выход - три различных состояния. Это означает, что вход : может воспринимать только информацию, записанную в дво­ичной система, а выход - информацию в троичной система. Или, иначе, будем говорить, что вход работает в двоичном ал­фавите (коде), а выход - в троичном алфавите. Соответствен­но будем говорить, что алфавит входа состоит из двух букв (например,0 и I), а алфавит выхода - из трех букв (напри­мер, 0, 1, 2). Если на вход 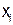в последовательные дискретные моменты времени поступает последовательность букв двоичного ал­фавита, скажем, 010001001, то будем называть эту последователь­ность словом в данном алфавите.

Под синхронностью работы автомата будем понимать тот факт, что если на входы системы в дискретные моменты времени поступает последовательность сигналов, то и на выходах в каждый момент реализуется точно по одной букве. Транзистор, например, можно рассматривать как синхронный автомат, перерабатывающий входную информацию в выходную, причем обе информации реализованы в дво­ичном алфавите.

Если на вход некоторого автомата синхронного действия по­ступает последовательность сигналов принимаю­щая значения из некоторого алфавита A, а на выходе наблюдается последовательность принимающая значения из не­которого алфавита В, то можно сказать, что автомат реализует некоторый оператор F,

Всякий синхронный автомат считается устройством без пред­восхищения, т.е. устройством, сигнал на выходе которого в мо­мент t зависит только от сигналов, поступивших не позднее этого момента.

Оператор F называется детерминированным, если в каждой мо­мент t выходной сигнал у (t) есть однозначная функция от слова

Детерминированный оператор преобразует всякое входное сло­во в слово той же длины, причем если первые К букв у двух вход­ных слов одинаковые, то одинаковыми будут и первые К букв у со­ответствующих выходных слов.

Наиболее интересными простейшими операторами является так называемые истинностный и константный операторы.

Истинностный оператор задает однозначное отображение y(t)= F(x(t)) т.е. это оператор без предвосхищения и без памяти, ставящий в соответствие в каждый момент t каждой вход­ной букве x(t) некоторую выходную букву у (t). Подобный опе­ратор может быть описан системой функций алгебры логики:

или же задан в виде некоторой формулы алгебры логики. Например, оператор транзистора задается функцией .

Константный оператор характеризуется тем, что любое вход­ное слово oн переводит в заданное (всегда од­но и то же) слово например, любая последовательность входных букв всегда переходит в последовательность OIOOOIIOOI...

Описывать работу автомата часто бывает удобно c помощью деревьев, позволяющих в нагляд­ной форме изображать входную и выходную информацию произволь­ного конечного автомата.

Пусть, например, входная информация является двоичной. Возьмем некоторую точку А и примем ее за корень некоторого дерева (рис. 7). Эту точку на­зывают также вершиной первого ранга. Проведём из 0 два отрез­ка, определяющих два возможных входных состояния автомата (О и I), называемых ребрами первого ранга. Из их концов, называемых вершинами второго ранга, проведем еще по два отрезка, называемые ребрами второго ранга, и т.д. Множество всех ребер k -го ранга образует k -и ярус де­рева (в данном случае - в двоичном алфавите). Если на вход автомата поступает последовательность сигналов х 1) = 1,x (2) =1, х(3) = 0, х(4)=1,...т.е. последовательность II0I... эта после­довательность на приведенном дереве изобразится путем, выделен­ным жирными стрелками. На этом же дереве можно изобразить и вы­ходную информацию. В таком случае дерево называется нагружен­ным. Пусть, например, выходная информация автомата, входная ин­формация которого изображена на рис. 7 в виде стрелок на дере­ве, выдается в троичном.коде (012), и пусть входной последова­тельности IIOI... отвечает выходная последовательность 1032... Чтобы получить нагруженное дерево, припишем соответствующим ребрам дерева входной информации буквы троичного алфавита вы­ходной последовательности (выходного слова) I0I2...

Легко видать, что любой оператор, задаваемый нагруженным деревом, является детерминированным и, наоборот, всякий детер­минированный оператор может быть задан в вида нагруженного де­рева.

Пусть 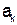- некоторая вершина ранга К дерева D. Ветвью ранге К дерева D назовём дерево , за корень которого примемы вершину . Если все дерево D задает некоторый детерминированнный оператор F, то дерево тоже задает детерминированный оператор 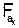, называемый остаточным оператором ранга К.

В этом случае исходный оператор можно считать остаточным опера­тором ранга I. Два оператора с одинаковым входным алфавитом различимы, если найдется хотя бы одно входное слово, которое перерабатывается ими в разные выходные слова. В противном слу­чав операторы неразличимы. У неразличимых операторов нагружен­ные деревья тождественны.

Реальные физические устройства, перерабатывающие дискрет­ную информацию, могут находиться лишь в конечном числе различ­ных состояний. В связи с этим имеет смысл среди всех детермини­рованных операторов выделить некоторый подкласс, моделирующий указанные физические устройства.

Определение. Детерминированный оператор называется ограни­ченно детерминированным (или оператором с конечной памятью), если во множестве всех его остаточных операторов имеется лишь конечное число попарно различимых операторов. Минимальное число попарно различимых операторов в этом случае называется весом оператора.

Пример. Всякий истинностный оператор имеет вес К = I, по­скольку он характеризуется тем, что каждой входной буква отве­чает вполне определенная выходная, а следовательно, в его дере­ве выходящие из любой вершины ребра нагружена одинаково. Про­стейшим примером подобного оператора может служить оператор, реализуемый транзистором; дерево этого оператора изображено на рис. 8.

Рис. 8

Ветви всех деревьев любого истинностного оператора попарно неразличимы.

Пример. Константный оператор (непериодический) служит при­мером оператора, имеющего вес К = . Этот оператор характери­зуется тем, что в его дереве все ветви одного ранга неразличи­мы, т.е. всем ребрам одинакового яруса приписывается одна и та же буква выходного алфавита. Это является следствием того, что выходная последовательность константного оператора фиксиро­вана, т.е. в каждый момент t = I, 2,... на выходе реализуется фиксированная буква y(k), зависящая только от k, а не от вход­ного сигнала. Например, пусть при двоичном входном и выходном кода на выходе всегда получается последовательность 10101001... (Дерево такого оператора показано на рис. 9.) Число попарно раз­личимых ветвей подобного дерева равно бесконечности, и все оста­точные операторы являются константными. Константный оператор не является ограниченно детерминированным (ОД). Можно показать, что любой ОД оператор можно реализовать в некоторой автомате синхронного действия.

Риc. 9

Базисом детерминированного оператора назовем любую систему его попарно различимых операторов, такую, что любой из остаточ­ных операторов содержится в этой системе. Оператор с весом К имеет базис из K операторов.

Перефразируя это определение в отношении дерева, можно сказать, что в дерево о максимальным числом К попарно различимых ветвей базис состоит из К вершин (или ветвей). Например, в изображенном на рис. 10 дереве базис состоит из двух ветвей, в качестве которых можно взять две ветви (две вершины) второго ранга. Вершины этого базиса обозначены через и .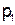

Если базис ОД оператора равен К, то можно ввести К -значный алфавит пометив вершины дерева оператора эти-ми буквами, задающими К различных состояний системы. Если система описывается ОД оператором, то всякий выходной сигнал y(t), который всегда может быть изображен на нагруженном дереве с отмеченными в его вершинах последовательными состояниями р(t), является однозначной функцией от текущего состояния p(t) и входного сигнала х (t). При этом следующее состояние системы p(t+1) также является однозначной функцией текущего входного сигнала и текущего состояния р(t). Таким образом, ОД оператор можно описать уравнениями (называемыми каноническими)

Изображенное выше дерево (с базисом 2) соответствует следующим каноническим уравнениям "двоичного счетчика":

В общем случае каждое из приведённых канонических уравне­ний является вектор-уравнением, в котором

Эти уравнения при заданных начальных условиях однозначным образом определяют ОД оператор, вес которого не превышает числа букв в алфавите состояний. По этим уравнениям легко строится нагруженное дерево, в котором неразличимы вершины, помеченные одной и той же буквой состоя­ния.

Любой конечный автомат можно описать каноническими уравне­ниями, приведенными выше. Реальные автоматические устройства обычно состоят из множества простейших устройств, называемых элементами. Каждый элемент представляет собой ячейку с внутренним алфавитом ,содержит m входных и n выходных

каналов и описывается каноническими уравнениями такого же вида. Отходящие от элемента концы каналов называют входными и выход­ными полюсами.

Входные и выходные алфавиты называют внешними алфавитами. Величину , где К - число букв внутреннего алфавита, на­зывают объемом внутренней памяти элемента автомата. Если алфа­вит состоит всего из одной буквы , то объем внутренней памя­ти равен нули, что имеет место, например, для истинностного оператора.

Схемой называют модель автомата, в которой определены эле­менты и их соединения; можно также сказать, что схема - это граф с ориентированными ребрами (каналами) и вершинами двух ти­пов: ячейками (характеризуемыми внутренними алфавитами) и полю­сами (характеризуемыми внешними алфавитами).

Рассмотрим некоторые из простых типовых элементов, из ко­торых составляют сложные схемы:

I. Двоичный счетчик с каноническим уравнениями

(Рис. II).

2. Сложение по модулю 2 (рис. 12)

 

Рис. 11

 

 

 

 

3. Элемент задержки (рис. 13)

y(t)=p(t), p(t+1)=x(t)

 

В уравнениях элемента задержки выходной сигнал не зависит от входного, а определяется только внутренним состоянием элемента. В таких случаях говорят, что выход не подчинен входу.

Из элементов можно составлять сложные схема, соединяя их полюса различным образом. При этом в схеме возможно образование обратных связей - ориентированных циклов (петель). Например, объединяя элементы Мс и , замкнув выход второго со входом первого, получаем схему, изображенную на рис. 14.

 

 

 

Рис. 14

 

 

 

Рис. 15

 

 

Однако следует избегать подобных схем, характеризующихся тем, что в них полюса в цикле попарно подчинены друг другу. Циклы необходимо строить так, чтобы хотя бы одан из полюсов цикла не подчинялся другим полюсам этого же цикла. Этого южно достичь, включив в цикл, например, элемент задержки . В изображенной схеме полюс оказывается не подчиненным полю­су , поскольку в уравнениях элемента задержки выход не за­висит от входа, а зависит лишь от внутреннего состояния эле­мента (рис. 15).

Говорят, что цикл (петля) правильный, если хотя бы один из составляющих его полюсов не подчинен ни одному из остальных. В противном случае цикл считается неправильным и в нем возника­ет порочный круг в передаче информации. Таким образом, схема, составленная из элементов, должна быть правильной.в том смысле, что в ней с физической точки зрения должны протекать естествен­ные процессы.

Будем говорить, что система уравнений правильна, если ока удовлетворяет следующим условиям:

I) система удовлетворяется для любых входных переменных x(t);

2) вектор выходных переменных является единственным;

3) оператор, описываемый уравнениями, удовлетворяющими условиям I) и 2), является ОД.

Если несколько схем без общих полюсов являются правильно организованными, что, в частности, предполагает правильность системы уравнений, то и формальная совокупность этих схем без каких-либо отождествлений их полюсов, представляется правильно организованной схемой.

Посмотрим теперь, что получится, если в правильно органи­зованной схеме отождествить некоторые из входов. Пусть, напри­мер, отождествлены входные полюса и . В результате число входов в схеме уменьшится "на единицу, а система уравнений по-прежнему останется правильной: в ней лишь две переменные и заменятся одной. С физической точки зрения допустимо так­же и объединение выходов; однако с рассматриваемых позиций идеализированного математического моделирования подобное объ­единение не имеет смысла.

Рассмотрим теперь условия сохранения правильной организации схемы в случав отождествления входных полюсов с входами. Пусть выходной полюс замкнут на входной полюс . В этом случае следует потребовать независимостъ выхода от входа . Канонические уравнения для подобным образом сформулированной схем могут быть получены из исходных уравнений, если в этих последних вместо 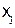подставить .

B результате в правой части кано­нически уравнений будет отсутствовать переменная .

Определение логической сети. Отдельный элемент определяет­ся как логическая сеть; совокупность двух логических сетей без общих полюсов тоже есть логическая сеть; логическая сеть оста­ется таковой при отождествлении выходного полюса с таким ее входным полюсом , которому выход не подчинен; логическая сеть, в которой отождествлены входы и , остается логичес­кой сетью.

Отвечавшая логической сети система уравнений является пра­вильной, задающей некоторый ОД оператор. Можно доказать следующее: чтобы схема была логической сетью, необходимо и достаточ­но, чтобы ни в какой полюс не втекало более одного выходного канала и чтобы в схеме не было неправильных петель. Отсюда,

в частности, следует, что всякая схема (без петель) в виде де­рева, в каждый полюс которой втекает не более одного выходного канала, есть логическая сеть.

Внутренним алфавитом логической сети, составленной из q, элементов, будет прямое произведение этих алфавитов, вклю­чающее букв, где 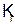- число букв внутреннего алфавита i -го элемента. А логарифм этого произведения определяет объем внутренней памяти логической сети. Таким образом, объем внут­ренней памяти сети равен сумме объемов внутренней памяти эле­ментов сети.

Рассмотрим теперь вопрос о физической реализуемости ОД операторов, ограничиваясь (без потери общности) случаем двоич­ного алфавита (0,1). Проще всего этот вопрос решается в отно­шении истинностного оператора, описываемого следующей системой функций алгебры логики:

Любая функция алгебры логика осуществима в той или иной логической сети, если имеются элементы, воплощающие отрицание и конъюнкцию или дезъюнкцию. Реализация функции алгебры логики, очевидно, возможна и при любом другом наборе элементов, обра­зующих полную систему, например, при наличии всего одного элемента, позволяющего получить функцию Шеффера. Таким образом, все истинностные операторы физически реализуемы.

Рассмотрим теперь общий случай построения ОД операторов, определяемых каноническими уравнениями

всегда можно реализовать канонические уравнения ОД оператора. Таким образом, при наличии полного набора элементов, позволяющего получать функции алгебры логики, и элемента задержки можно пост­роить логическую сеть, реализующую ОД оператор. Поскольку элементы задержки физически осуществимы, то возможно построение и любого ОД оператора.

 

 

ЛИТЕРАТУРА

1. Клики С.К. Математическая логика: Пер. о франц. М,: Мир, 1973.

2. Кобринский Н.Е., Трахтенброт Б.А. Введение в теорию ко­нечных автоматов. U.: Физшттиз, 1962.

3. Мендельсон Э. Введение в математическую логику: Пер. с англ. М.: Наука, 1984.

4. Новиков П.С. Элементы математической логики. М.: 1973.

5. Трахтенброт Б.А. Алгоритмы и вычислительные автоматы. М.: Сов. радио, 1974.

6. Шолоиов I.A. Основы теории дискретных логических и вы­числительных устройств. II.: Наука, 1980.

7. Яблонский С.B. Введение в дискретную математику. М,: Наука, 1966.