Задачи линейного программирования решаются с помощью симплексного метода с искусственным базисом в том случае, когда в условиях задачи имеются ограничения типа «≥» или «=». При канонической форме записи таких ограничений возникает необходимость введения дополнительной переменной с отрицательным знаком, что противоречит условию неотрицательности переменных. Так как отрицательную дополнительную переменную нельзя вводить в базис, то в этом случае естественного базиса задачи не существует и её нельзя решить по алгоритму симплексного метода.
Для решения таких задач применяют алгоритм симплексного метода с искусственным базисом. Искусственный базис создают путем введения в левую часть уравнения в канонической форме искусственной переменной y.
Так, если по условиям задачи имеется ограничение типа «≥» (или «=»):
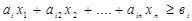, (3.18)
то в канонической форме записи оно выглядит:
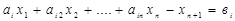, (3.19)
а с введением искусственной переменной «у» оно будет представлено в виде:
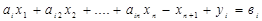. (3.20)
В первой симплексной таблице искусственные переменные «у i » вводятся в базис, как и положительные дополнительные переменные x n+1. Для последующего исключения искусственных переменных «у i » из оптимального плана в функцию цели их вводят с очень большими по абсолютной величине коэффициентами. При этом коэффициенту присваивается знак «-», если задача решается на максимум, и знак «+», если задача решается на минимум.
В симплексной таблице в дополнение к индексной строке m+1 вводится строка m+2. Значения элементов для обеих индексных строк рассчитывается по формуле (3.14). При этом в строку m+2 записываются слагаемые, которые содержат величину М. В связи с этим строку m+2 называют М-строкой, а сам метод называют М-методом.
|
|
Порядок заполнения первой симплексной таблицы в М-методе не отличается от порядка, рассмотренного в симплексном методе за исключением заполнения m+2 строки.
Проверка плана на оптимальность осуществляется по тем же признакам, что описаны выше, но по коэффициентам индексной m+2 строки до её выбытия из расчетов.
Если план не оптимален, то для целей его улучшения (перерасчета) выбираются ключевые К-столбец и l -строка. Ключевой столбец выбирают, руководствуясь коэффициентами m+2 строки, не обращая внимания на строку m+1. Ключевую l -строку выбирают по минимальному положительному отношению, т.е. как и в обычном симплексном методе.
В процессе последовательного улучшения планов искусственные переменные «у» будут выведены из базиса и их столбцы вычеркиваются, а коэффициенты m+2 строки будут равны «0» и в ней отпадает необходимость. В базисе останутся только основные и положительные дополнительные переменные, поэтому дальнейший поиск оптимального плана осуществляется по алгоритму симплексного метода, руководствуясь m+1 строкой.
При решении задач М-методом соблюдается та же последовательность (этапы), что и в симплексном методе.
Пример решения задачи симплексным методом с искусственным базисом.
1. Постановка задачи
В хозяйстве планируется использовать массив пашни площадью 1000 га под посевы: пшеницы (Х1), овса (Х2) и ячменя (Х3).
Объем производства зерна ячменя должен быть равен 3200 ц, а пшеницы не менее 8000 ц. Затраты труда на производство продукции на данном массиве пашни должны составлять не более 4000 чел. - дней.
|
|
Необходимо составить оптимальную структуру посевов указанных культур, обеспечивающих максимальную стоимость валовой продукции (Zmax).
Исходную информацию представим в виде таблицы (3.8).
2. Составление экономико-математической модели задачи.
В соответствии с условиями задачи экономико-математическая модель в развернутом виде выглядит следующим образом:
Zmax =84Х1+72Х2+56Х3.
пи условиях: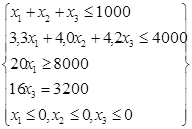 
(3.21)
Таблица 3.8
Исходная информация
| № п/п | Показатели | Единица измерения | Затраты ресурсов на 1 га посевов культур | Тип ограничения | Размер ресурса | ||
| пшеница | овес | ячмень | |||||
| 1. | Площадь пашни | га | ≤ | ||||
| 2. | Урожайность | ц/га | |||||
| 3. | Объем производства пшеницы | ц | - | - | ≥ | ||
| ячменя | ц | - | - | = | |||
| 4. | Трудовые ресурсы | чел. - дней | 3,3 | 4,0 | 4,2 | ≤ | |
| 5. | Стоимость валовой продукции | тыс. руб. | → | макс. |
С введением дополнительных переменных задача примет следующий вид:
Zmax =84Х1+72Х2+56Х3+0∙Х4+0∙Х5+0∙Х6-М(у1+ у2)
пи условиях: 
(3.22)
Введем в уравнения, полученные из исходной системы неравенств и имеющие вначале ограничения типа «≥» или «=», искусственные переменные у1 и у2:
Zmax =84Х1+72Х2+56Х3+0Х4+0Х5-М(у1+ у2)
пи условиях: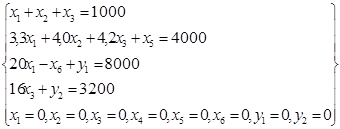 
(3.23)
3. Составление исходного плана (первой симплексной таблицы)
Исходный план (первая симплексная таблица) заполняются в следующей последовательности (таблица 3.9):
- в базис (столбец 2) из системы уравнений (3.23) вводим дополнительные переменные Х4, Х5, и искусственные переменные у1, у2;
|
|
- в столбец 3 (Сi) записываются коэффициенты целевой функции при дополнительных и искусственных переменных, вошедших в базис. При дополнительных переменных это нули, а при искусственных переменных это коэффициент М (с положительным знаком при Z→min и с отрицательным Z→max);
- в столбец 4 (вi) записываются значения свободных ресурсов (свободных членов);
- в столбцы 5-12 по строкам (ограничениям) записываются коэффициенты (аij) при основных, дополнительных и искусственных переменных;
- строки m+1 и m+2 заполняются коэффициентами, рассчитанными по формуле (3.14). Для столбца вi (столбец 4) данная формула примет вид:
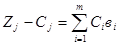, (3.24)
Рассчитанные по данной формуле значения записываются в строку m+1 – без коэффициентов М, а в строку m+2 – с коэффициентами М. Так, для столбца 4 (вi) для строк m+1 и m+2 значения рассчитаны следующим образом:
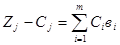=0∙1000+0∙4000+(М∙8000)+(-М∙3200)=0-11200М.
Исходя из этого «0» записываем в строку m+1, а значение -11200М в строку m+2.
Для столбца 5 (аналогично и для столбцов 6-12 таблицы 3.5) коэффициенты для заполнения строк m+1 и m+2 получены следующим образом:
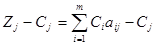=0∙1+0∙3,3+(-М∙20)+(-М∙0)-84=-84-20М.
Коэффициент -84 записываем по строке m+1, а -20 по строке m+2;
- столбец 13 («сумма по строке») заполняется путем суммирования коэффициентов столбцов 4-12 по строке.
После заполнения данной таблицы можно переходить к анализу исходного плана на оптимальность.
4. Анализ плана на оптимальность
До тех пор, пока в базисе имеются искусственные переменные (у1, у2), проверка плана на оптимальность осуществляется по коэффициентам m+2 строки.
В нашем примере исходный план (таблица 3.9) не оптимален, т.к. в m+2 строке стоят отрицательные коэффициенты М. Они должны быть выведены из m+2 строки в процессе решений.
После выведения из базиса искусственных переменных (у1 и у2) план на оптимальность анализируется по коэффициентам m+1 строки, как и в симплексном методе.
В рассматриваемой задаче искусственные переменные были выведены из базиса в таблицах 3.10-3.11. Поэтому четвертая и пятая симплексные таблицы (таблицы 3.12-3.13) анализировались на оптимальность по коэффициентам m+1 строки. Оптимальным является план в пятой симплексной таблице (таблица 3.13), т.к. в m+1 строке нет отрицательных коэффициентов.
5. Улучшение плана
Для улучшения исходного плана (таблица 3.9) в качестве ключевого К-столбца выбран столбец 5 (переменная Х1), имеющий в m+2 строке наибольший по абсолютной величине отрицательный коэффициент (-20М).
По наименьшему положительному отношению (8000׃20=400) в столбце 14 выбираем ключевую l -строку.
Общий порядок улучшения плана в симплексном методе с искусственным базисом мало чем отличается от порядка улучшения плана в обычном симплексном методе. Особенностью улучшения плана в М-методе является то, что при выведении из базиса искусственной переменной (y i) её столбец вычеркивается из дальнейшего рассмотрения. Однако для получения правильной суммы коэффициентов по строке (для заполнения столбца 13 и сравнения её со значением по строке в столбце 15) необходимо выполнять расчеты коэффициентов аij и по этим столбцам (см. таблицы 3.10-3.13).
Первые четыре симплексные таблицы (таблицы 3.9-3.12) содержали неоптимальные планы, поэтому по уже известному алгоритму было выполнено их улучшение.
6. Контроль правильности решения задачи
Контроль правильности решения расчетов выполнен посредством сравнения значений в столбцах 13 и 15 по каждой из строк в симплексных таблицах (таблицы 3.10 -3.13).
Контроль правильности решения задачи выполняется также путем подстановки полученных численных значений основных и дополнительных переменных, вошедших в базис, в систему неравенств (3.21).
Если условия неравенств соблюдается, то полученные значения базисных переменных допустимы и соответствуют оптимальным.
7. Анализ оптимального решения задач и значений коэффициентов последней симплексной таблицы
Численные значения переменных, составляющие оптимальное решение задачи, содержатся в столбце вi (см. столбец 4 таблицы 3.13). В базис последней симплексной таблицы могут входить как основные, так и дополнительные переменные.
Их экономический смысл заключается в следующем: основные переменные выражают величины использованных ресурсов, а дополнительные переменные – недоиспользованные (при ограничении типа «≤») или перерасходованные (при ограничении типа «≥») ресурсы.
Так, в рассматриваемой задаче численные значения основных переменных Х1=800 и Х3=200 выражают оптимальные размеры посевных площадей, соответственно пшеницы и ячменя. Основная переменная Х2 не вошла в базис, что указывает на нецелесообразность посева овса.
Дополнительная переменная Х5=480 чел.- дн. показывает величину недоиспользованных трудозатрат, а дополнительная переменная Х6=8000 ц, показывает величину дополнительного объема производства пшеницы, превышающего установленное ограничение ≥8000 ц (см. формулу 3.21).
Оптимальное значение функции цели стоит на пересечении столбца вi (столбец 4 таблицы 3.13) и m+1 строки. Оно составляет 78400 тыс. руб. и выражает максимальную стоимость валовой продукции при поставленных в задаче условиях.