РЕШЕНИЕ ЗАДАЧ ПРОГРАММИРОВАНИЯ СИМПЛЕКСНЫМ МЕТОДОМ

СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

 

Симплексный метод линейного программирования относится к универсальным методам, обеспечивающим эффективное решение разнообразных землеустроительных и других экономических задач. Универсальность данного метода проявляется в том, что он позволяет решать задачи различной размерности, в которых технико-экономические коэффициенты (α_ij) при переменных (Х _ij) выражены в разных единицах измерения.

Сущность симплексного метода заключается в нахождении оптимального решения задачи путем последовательного рассмотрения и анализа ее допустимых базисных решений. Геометрически каждое допустимое базисное решение соответствует одной из вершин многоугольника в n –мерном пространстве ограничивающего в соответствии с условиями задачи область допустимых решений (ОДР).

В процессе решения задачи на каждой итерации осуществляется переход из одной вершины ОДР в смежную, связанную с не худшим значением целевой функции. Для этого используется процедура метода главных элементов. Количество итераций, необходимых для получения оптимального решения, находится в пределах от m до 2m, где m -количество ограничений в задаче.

Экономико-математические модели задач линейного программирования, решаемых симплексным методом, могут быть представлены в структурной форме или в развернутом виде. Структурная модель задачи записывается следующим образом:

Найти Z_max,min = (3.1)

при условиях: / i=1,2,…m/ (3.2)

Если подробно описать все условия задачи в виде системы неравенств и уравнений, то такая экономико-математическая модель называется развернутой.

В зависимости от сложности решаемых задач экономико-математические модели могут иметь разные размеры, которые определяются произведением количества ограничений на количество переменных (m∙n).

РЕШЕНИЕ ЗАДАЧ ПРОГРАММИРОВАНИЯ СИМПЛЕКСНЫМ МЕТОДОМ

Экономико-математические модели линейного программирования структурно состоят из трех частей: целевой функции, системы ограничений и условия не отрицательности переменных. Целевая функция выражает основное условие задачи, критерий её оптимальности, ориентированный на максимум или на минимум.

Система ограничений в экономико-математических моделях задач, решаемых симплексным методом, записывается в стандартной форме, т.е. в виде неравенств и уравнений. В зависимости от типа ограничений задачи решаются по алгоритму симплексного метода, или алгоритму данного метода с искусственным базисом.

Рассмотрим алгоритм решения задач симплексным методом, который применяется и при решении задач с искусственным базисом за исключением некоторых особенностей алгоритма на начальных этапах их решения.

Методика решения задач симплексным методом предусматривает соблюдение следующих этапов их решения:

1. Постановка задачи;

2. Составление экономико-математические модели задачи;

3. Составление исходного плана (первой симплексной таблицы);

4. Анализ плана на оптимальность;

5. Улучшение плана;

6. Контроль правильности решения задачи;

7. Анализ оптимального решения задачи и формулирование ответа.

Для более наглядного представления алгоритма симплексного метода решим задачу, выраженную в условных единицах измерения.

 

1. Постановка задачи

При постановке задачи формулируется (словесно): оптимальные значения, каких неизвестных необходимо найти, при каких условиях (ограничениях) по видам и размерам ресурсов, какая функция цели и на что она ориентирована (на максимум или минимум). Например, необходимо определить оптимальное сочетание объемов производства трех видов продукции (Х₁, Х₂, Х₃) при имеющихся в хозяйстве трех видах ресурсов в размере в₁=100, в₂=40, в₃=50 (это могут быть трудовые ресурсы, удобрения, капиталовложения и т.п.) с целью получения максимальной денежной выручки (или валовой продукции и т.п.).

 

2. Составление экономико-математические модели задачи

Экономико-математическая модель в симплексном методе составляется в следующей последовательности:

- записывается уравнение функции цели, правая часть которого представляет собой сумму произведений искомых неизвестных (Х₁, Х₂, Х₃) на соответствующие им по условиям задачи коэффициенты целевой функции:

Z_max =20Х₁+10Х₂+30Х₃ (3.3)

- условия задачи записываются в виде неравенств с ограничениями типа ≤. Каждое из неравенств выражает собой ограничения по одному из видов ресурсов, поэтому в левой части неравенства проставляют искомые переменные с коэффициентами, выражающими расход данного вида ресурса на единицу искомой переменной или, наоборот, выход данного вида ресурса с единицы соответствующей переменной. В правой части неравенства проставляется тип ограничения ≤ и величина соответствующего вида ресурса;

- количество неравенств в системе ограничений обусловлено условиями задачи. При записи неравенств необходимо контролировать правильность их оформления: технико-экономические коэффициенты при переменных, состав переменных (в левой части неравенства), вид и размер ресурса (в правой части неравенства) должны строго соответствовать условиям задачи и характеру её постановки.

Таким образом, система ограничений выглядит следующим образом:

3Х₁+5Х₂+8Х₃≤100 (3.4)

2,5Х₁+3Х₂+6Х₃≤40 (3.5)

2Х₁+4Х₂+3Х₃≤50 (3.6)

- после записи основных условий задачи в виде системы ограничений обязательно формулируется условие не отрицательности переменных, так как алгоритм симплексного метода позволяет решать задачи только с положительными значениями переменных (Х _j):

Х₁≤0; Х₂≤0; Х₃≤0. (3.7)

Представленная выше форма записи условий задачи в виде неравенств называется стандартной. Для заполнения первой симплексной таблицы (исходного плана) необходимо перейти от стандартной формы записи условий задачи к канонической, а от неё – к симплексной.

Каноническая форма записи условий задачи предусматривает преобразование неравенств (стандартной формы записи) в уравнения, для этого в левую часть каждого из неравенств вводят дополнительные переменные со следующими знаками: с плюсом, если неравенство типа «≤ » и с минусом, если неравенство типа «≥ ». Дополнительным переменным (Х₄, Х₅, Х₆) поочередно присваиваются номера, продолжающие нумерацию основных переменных (Х₁, Х₂, Х₃). В уравнение дополнительные переменные вводятся с коэффициентом 1, а в целевую функцию с нулевыми коэффициентами для исключения их влияния на результаты решения задачи.

Преобразуем приведенную выше систему неравенств в систему уравнений:

3Х₁+5Х₂+8Х₃+Х₄≤100 (3.8)

2,5Х₁+3Х₂+6Х₃+Х₅≤40 (3.9)

2Х₁+4Х₂+3Х₃+Х₆≤50 (3.10)

Для дальнейшего преобразования канонической формы записи в симплексную система уравнений решается относительно дополнительных переменных:

Х₄=100-(3Х₁+5Х₂+8Х₃) (3.11)

Х₅=40-(2,5Х₁+3Х₂+6Х₃) (3.12)

Х₆=50-(2Х₁+4Х₂+3Х₃) (3.13)

Исходя из симплексной формы записи условий задачи, становится ясен экономический смысл дополнительных переменных. На начальном этапе решения задачи принимается условие, что основные переменные равны нулю, а значения дополнительных переменных, исходя из симплексной формы записи, будут равны величинам ресурсов. В нашем примере: при Х₁=0, Х₂=0, Х₃=0 будем иметь Х₄=100, Х₅=40, Х₆=50.

В экономическом отношении это означает, что пока не реализовано ни одно из мероприятий, намечаемых по условиям задачи, ресурсы остаются неиспользованными. Исходя из данной установки, создается исходный базис (исходное условие), на основе которого начинается поиск оптимального решения задачи из числа допустимых её решений.

Если в системе уравнений отражающих условие задачи, количество переменных (n) больше количества ограничений (m), то система имеет множество решений. При этом допустимым решением системы называется любой набор переменных, удовлетворяющих условиям задачи, а допустимым базисным решением – допустимое решение, содержащее не больше, чем m не нулевых переменных. Поэтому первая симплексная таблица (исходный план) содержит допустимое базисное решение задачи. Рассмотрим порядок заполнения первой симплексной таблицы (таблица 3.1).

 

3. Составление исходного плана (первой симплексной таблицы)

Содержание первой симплексной таблицы и порядок её заполнения рассмотрим последовательно по столбцам и строкам.

Столбец 1 – приводится нумерация строк, соответствующая нумерации ограничений в задаче.

Столбец 2 – записывается только дополнительные переменные (Х₄, Х₅, Х₆), т.к. они составляют исходный базис для начала решения задачи.

Столбец 3 – записываются коэффициенты целевой функции при дополнительных переменных, вошедших в базис. Они равны нулю, т.к. дополнительные переменные (Х₄, Х₅, Х₆), вошедшие в базис, в целевую функцию введены с нулевыми коэффициентами (С_ij =0) для исключения влияния дополнительных переменных на величину функции цели (Z).

Столбец 4 – записывается значение ресурсов (свободных членов), стоящих в правой части соответствующего неравенства (уравнения). Исходя из симплексной формы записи условий рассматриваемой задачи дополнительные переменные, вошедшие в базис, выражают неиспользованные ресурсы, поэтому: Х₄=100, Х₅=40, Х₆=50. Следовательно, в столбец свободных членов (в _j) записываются исходные величины ресурсов.

Столбцы 5-7 – это столбцы основных переменных (соответственно, Х₁, Х₂, Х₃). В них на пересечении со строками соответствующих уравнений проставляются технико-экономические коэффициенты (а_ij), стоящие в данных уравнениях при каждой из основных переменных. Так, из первого уравнения (3.8) 3Х₁+5Х₂+8Х₃+Х₄=100 коэффициенты при основных переменных (Х₁, Х₂, Х₃), соответственно 3,5 и 8 занесены в столбцы данных переменных по первой строке таблицы (3.1).

Столбцы 8-10 – это столбцы дополнительных переменных (Х₄, Х₅, Х₆), в которых проставляются коэффициенты при данных переменных по каждому уравнению (соответствующим им строкам таблицы), в которое входит соответствующая переменная. Так, дополнительная переменная Х₄ входит в первое уравнение с коэффициентом 1, поэтому данный коэффициент записываем в столбец 8 (это столбец Х₄) по первой строке таблицы (это строка первого уравнения 3.8). В остальных столбцах дополнительных переменных Х₅ и Х₆ (столбцы 9,10) по первой строке проставляем нули, т.к. данные дополнительные переменные не входят в первое уравнение.

Столбец 11 – в него записывается суммы, полученные путем сложения свободного члена (в _j) и коэффициентов (а_ij) по соответствующей строке таблицы. Так, если сложить по первой строке таблицы (3.1) свободный член и коэффициенты (100+3+5+8+1=117), то получим число 117, которое и записано в столбце 11. аналогичным образом получаем значения для столбца 11 и по остальным строкам таблицы.

Столбец 12 – в него записываются значения, полученные в результате построчного деления значений свободных членов (в _j) на положительные коэффициенты ключевого (k -го) столбца.

Для выполнения таких расчетов необходимо предварительно выбрать ключевой столбец (k –й столбец). В качестве ключевого (k -го) выбирается столбец (из числа столбцов основных переменных Х₁, Х₂, Х₃, т.е. столбцов 5-7), по которому в индексной (m+n) строке таблицы стоит максимальное по абсолютной величине: отрицательное число при решении задачи на максимум и, наоборот, положительное число, при решении задачи на минимум.

В данной задаче таким максимальным по абсолютной величине числом является -30 (т.к. Z→max), стоящий в столбце основной переменной Х₃ (столбец 7), следовательно, это и будет ключевой столбец. Присвоим ему литер «К».

Теперь можно выполнить расчеты для заполнения столбца 12. По первой строке указанное отношение получаем, разделив свободный член 100 (в ₁ =100) на положительный коэффициент 8 (в₁ =8), стоящий по данной строке в ключевом столбце. Оно равно 12,5 (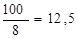). Запишем его в таблицу 3.1.

Аналогично определяем остальные значения для столбца 12.

Значения, записываемые в столбце 12 служат, в последующем основанием для выбора ключевой строки (l -строки), используемой вместе с ключевым (k- столбцом) столбцом для получения следующей симплексной таблицы (улучшенного плана).

Столбец m+1 – это индексная строка симплексной таблицы. На пересечении m+1 строки и столбца основных членов в _i (столбец 4), записывается численное значение функции цели (Z). В первой симплексной таблице (3.1) оно равно нулю (Z =0).

Все остальные элементы индексной (m+1) строки рассчитываются по формуле:

, (3.14)

где С_i – коэффициенты целевой функции при переменных, вошедших в базис;

C_j - коэффициенты целевой функции при переменных (Х _ij), по столбцам которых выполняется расчет;

а_ij – технико-экономические коэффициенты при переменных Х _j, стоящих в i -м ограничении.

Так, для столбца переменной Х₁ (столбец 3) элемент индексной строки будет рассчитан следующим образом:

Z₁-C₁ = (0∙3+0∙2,5+0∙2)-20=-20.

Так же рассчитываются остальные элементы индексной строки (для столбцов 5-10). В столбец 11 проставляется сумма элементов по индексной строке (-60).

Для упрощения расчетов часто при заполнении индексной строки первой симплексной таблицы используют следующий подход: при решении задачи на максимум в индексной строке записываются коэффициенты целевой функции (С_j), стоящие при основных переменных, со знаком «-», а при решении задачи на минимум – со знаком «+».

Заполненная первая симплексная таблица (3.1) представляет собой исходный план, который анализируется на оптимальность.

 

4. Анализ плана на оптимальность

Признаком оптимальности опорного (как исходного, так и последующих) плана является отсутствие в индексной (m+1) строке при решении задачи на минимум – положительных коэффициентов или нулей. Если это условие не выполняется, то план не оптимален и необходимо его улучшать.

В рассматриваемой задаче, решаемой на максимум, исходный план (таблица 3.1) не оптимален, т.к. в индексной строке имеются отрицательные коэффициенты (-20, -10, -30). В связи с этим его необходимо улучшать.

 

5. Улучшение плана

Новый, улучшенный план, получают на основе преобразования неоптимального плана. Вычислительная процедура улучшения плана заключается в выведении из базиса неоптимального плана одной из базисных переменных и введение в него новой, небазисной переменной. Для осуществления этой процедуры в неоптимальном (улучшаемом плане, т.е. в первой симплексной таблице) выбирают ключевой К-столбец и ключевую l -строку (таблица 3.1).

Ключевой столбец (К-столбец) выбирают, как было отмечено выше, по наибольшему по абсолютной величине: отрицательному коэффициенту индексной строки при решении задачи на максимум, и положительному коэффициенту при решении задачи на минимум.

В первой симплексной таблице (неоптимальном плане) в качестве ключевого нами выбран столбец переменной Х₃ (столбец 7), в котором по индексной строке стоит наибольший по абсолютной величине отрицательный коэффициент -30 (Z_max).

Ключевая строка (l -строка) выбирается по минимальному положительному коэффициенту, стоящему в столбце 12. В первой симплексной таблице рассматриваемой задачи в качестве ключевой l -строки выбрана вторая строка, по которой в столбце 12 стоит наименьший положительный коэффициент (6,67).

Коэффициент, стоящий на пересечении ключевой строки и ключевого столбца называется главным или генеральным элементом (a_lk).

Новую симплексную таблицу (улучшенный план) с новым базисным решением составляют в следующей последовательности:

- вычерчивают новую симплексную таблицу (3.2) по форме первой таблицы, добавляя столбец 13 (для контроля правильности вычислений). Вместо базисной переменной, стоявшей в базисе (столбец 2) по ключевой l -строке предыдущей таблицы в новую таблицу записывают переменную Х _j, столбец которой выбран в качестве ключевого. Этим самым в базис новой симплексной таблицы вводится новая базисная переменная, а прежняя – выводится из базиса;

- в столбец 3, рядом с новой переменной, введенной в базис, записывают её коэффициент целевой функции. Остальные базисные переменные и их коэффициенты целевой функции (столбцы 2 и 3) переписываются в новую таблицу из предыдущей без изменения;

- элементы () для заполнения в новой таблице строки, стоящей на месте ключевой l -строки предыдущей таблицы, вычисляются как отношение соответствующего элемента (a_lj) ключевой l -строки на главный элемент (a_lk) предыдущей таблицы, т.е. по формуле:

, (3.15)

- элементы остальных строк новой симплексной таблицы, за исключением строки, стоящей на месте бывшей ключевой l -строки, пересчитываются по одной из следующих формул:

, () (3.16)

или «способом конверта»

, () (3.17)

где , а_ij – однотипные коэффициенты, соответственно новой и предыдущей симплексной таблиц;

, а_lj – коэффициенты строки, стоящей в новой таблице на месте бывшей ключевой l -строки и, соответственно, коэффициенты ключевой l -строки в предыдущей таблице;

a_ik – коэффициенты ключевого К-столбца предыдущей симплексной таблицы;

a_lk – главный (генеральный) элемент предыдущей симплексной таблицы, стоящий на пересечении ключевых l -строки и К-столбца.

Расчеты по указанным выше формулам выполняются для заполнения всех строк новой симплексной таблицы, включая индексную (m+1) строку, но исключая ключевую l -строку.

В соответствии с вышеизложенным выполнены расчеты по улучшению первого и второго планов (таблицы 3.1 и 3.2) и получен оптимальный план (таблица 3.3).

Таблица 3.1

Первая симплексная таблица

 

Номера строк (ограничений), i	Номера переменных, вошедших в базис, Xn+i	Коэффициенты целевой функции при базисной переменной, Сi	Свободные члены (ресурсы), вi	Коэффициенты целевой функции, С j	Сумма по строке	Отношение
Коэффициенты при небазисных переменных	Коэффициенты при базисных переменных
Х1	Х2	Х3	Х4	Х5	Х6
	Х4										12,5
	Х5									52,5	6,67
	Х6										16,67
m+1	Zj-Cj		-20	-10	-30				-60

 

Таблица 3.2

Вторая симплексная таблица

 

i	Базис, Xn+i	Сi	вi							Сумма по строке		Контроль
Х1	Х2	Х3	Х4	Х5	Х6
	Х4		46,66	-0,333				-1,333		47,00	-	47,00
	Х3		6,667	0,417	0,5			0,167		8,751	15,86	8,751
	Х6			0,750	2,5			-0,5		33,750		33,750
m+1				-7,5						202,500	-	202,500

 

Таблица 3.3

Третья симплексная таблица

 

i	Базис, Xn+i	Сi	вi							Сумма по строке		Контроль
Х1	Х2	Х3	Х4	Х5	Х6
	Х4		51,990		1,399	0,799		-1,199		53,989		53,989
	Х1		15,988		1,199	2,398		0,400		20,985		20,985
	Х6		18,010		1,600	-1,799		-0,799		18,012		18,012
m+1			319,909		13,993	17,985		8,003		359,890		359,890

 

6. Контроль правильности решения задачи

Контроль правильности задачи должен осуществляться на всех этапах её решения: от составления экономико-математической модели задачи до анализа оптимального её решения.

В порядке осуществления текущего контроля правильности решения задачи и исключения «зацикливания», в поиске оптимального её решения необходимо иметь в виду следующее:

- если в ключевом К-столбце все коэффициенты (a_ik) отрицательные, то решения задачи не существует;

- если в столбце свободных членов (ресурсов) имеются нули, то при последующем решении задачи может произойти зацикливание (вырождение). Для преодоления вырожденности плана нули заменяют на малые положительные числа, не оказывающие влияния на результаты решения задачи;

- признаком возможной вырожденности плана также является наличие двух равных минимальных положительных отношений (в столбце 12) при выборе ключевой l -строки. Для преодоления вырожденности плана по данному признаку необходимо в качестве ключевой l -строки выбирать ту, по которой в ключевом К-столбце стоит наибольший положительный коэффициент;

- начиная со второй симплексной таблицы, следует ввести дополнительный столбец «контроль» (столбец 13), элементы которого вычисляются по формулам (3.16 и 3.17) на основе использования соответствующих элементов столбца 11 и предыдущей таблицы.

В каждой из симплексных таблиц, начиная со второй, элементы 11 и 13 по строкам должны полностью совпадать. В случае несовпадения даже одного из элементов необходимо проверить правильность расчета значений элементов данной таблицы по описанному выше алгоритму.

Если перечисленные условия контроля соблюдены, то это гарантирует получение оптимального решения задачи. Контроль оптимального плана осуществляется в процессе его анализа.

 

7. Анализ оптимального решения задачи и формулирование ответа

Оптимальное решение задачи содержится в последней третьей симплексной таблице, не имеющей в индексной строке отрицательных элементов, так как задача решалась на максимум.

В столбце 2 последней симплексной таблицы (таблица 3.3) содержатся переменные, а в столбце 4 (в_i) их численные значения, составляющие оптимальное решение задачи. В нашем примере: Х₁=15,988; Х₄=51,990; Х₆=18,010. При этом переменные, вошедшие в базис в последней симплексной таблице, имеют следующий смысл:

- основные переменные (в нашем примере Х₁=15,988) выражают размеры использованных ресурсов;

- дополнительные переменные (Х₄=51,990, Х₆=18,010) выражают размеры неиспользованных ресурсов в зависимости от того, в ограничении по какому виду ресурса они стоят.

Для контроля правильности решения задачи значения переменных, вошедших в базис, подставляются в соответствующие им уравнения, и проверяется соблюдение условия равенства. Если, в рассматриваемой задаче, поставить значения Х₁, Х₄, Х₆ в систему уравнений (3.8-3.10), получим следующее:

3Х₁+5Х₂+8Х₃+Х₄=3∙15,988+51,990=99,954=100

2,5Х₁+3Х₂+6Х₃+Х₅=2,5∙15,988=39,97=40

2Х₁+4Х₂+3Х₃+Х₆=2∙15,988+18,010=49,986=50

В результате постановки указанных переменных в уравнения видно, что условие равенства соблюдается, т.е. задача решена правильно. Полученное значение основной переменной Х₁=15,988 является оптимальным при поставленных в задаче условиях, обеспечивающим максимальное значение целевой функции (Z_опт). Оптимальное значение функции цели находится в индексной строке (m+1) по столбцу в_i =319,909.

Остальные переменные, не вошедшие в базис, равны нулю, т.к. при заданных условиях задачи мероприятия, обозначенные основными переменными Х₂ и Х₃, оказались неэффективными.

Исходя из содержания последней симплексной таблицы (оптимального плана) ответ можно сформулировать следующим образом: оптимальным планом предусматривается проведение мероприятия, соответствующего Х₁=15,988 единиц, что обеспечивает получение максимального значения функции цели при заданных размерах ресурсов, равное 319,909 единиц.

 

ТЕХНОЛОГИЯ РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ПОМОЩЬЮ НАДСТРОЙКИ ПОИСК РЕШЕНИЯ В ПРОГРАММЕ EXCEL

Идея симплекс метода (последовательного улучшения) заключается в том, что начиная с некоторого исходного опорного решения, осуществляется последовательно направленное перемещение по опорным решениям задачи к оптимальным. Симплекс-метод является универсальным, так как позволяет решить практически любую задачу линейного программирования, заданную в каноническом виде /2/.

ПРИМЕР РЕШЕНИЯ. В хозяйстве имеется три вида сельскохозяйственных угодий: пастбище, сенокос, пашня, на которых производят 3 вида сельскохозяйственной продукции. На производство требуется 4 вида ресурсов: площадь сельскохозяйственных угодий, трудовые ресурсы, минеральные удобрения, оросительная вода. Необходимо составить план производства трёх видов продукции, который обеспечит получение ее максимального количества в стоимостном выражении в условиях ограниченности ресурсов. Исходная информация представлена в таблице 3.4.

Таблица 3.4

Исходные данные задачи

 

Вид ресурса	Единицы измерения	Запасы	Коэффициент затрат ресурсов для производства единицы продукции
пастбище	сенокос	пашня
Площадь сельскохозяйственных угодий	га		0,01	0,04	0,02
Трудовые ресурсы	чел.-дн		0,3
Минеральные удобрения	кг		1,5
Оросительная вода	м3		0,2	0,25	0,3
Стоимость реализации продукции	руб.

 

Обозначим объем продукции с пастбищ – х₁, с сенокосов – х₂, с пашни – х₃. С учетом этих обозначений математическая модель задачи имеет следующий вид:

Z =15х₁+50х₂+100х₃→max.

Решим задачу с использованием поиска решения. Поиск решения – это надстройка Excel, которая позволяет решать оптимизационные задачи.

Введем исходные данные в таблицу 3.5.

Таблица 3.5

Данные задачи, представленные в виде таблицы

 

х1	х2	х3
0,01	0,04	0,02
0,3
1,5
0,2	0,25	0,3

 

Поместим курсор в ячейку Е3, нажмем на кнопку мастер функций. На экране появится диалоговое окно мастера функций (рис. 3.1).

 

Рис. 3.1 - Окно мастера функий

В окне функции выбираем СУММПРОИЗВ, и на экране появляется диалоговое окно СУММПРОИЗВ. В строку массив 1 введем $A$2:$С$2, в строку массив 2 – A3:С3.

 

Рис. 1.2 - Окно СУММПРОИЗВ

Введем зависимости для ограничений. Выделим ячейку D3, скопируем и вставим в содержимое ячеек по данному столбцу до ячейки D7. Полученная таблица будет иметь вид:

Таблица 3.6

Таблица зависимостей для ограничений

 

х1	х2	х3
0,01	0,04	0,02
0,3
1,5
0,2	0,25	0,3

 

Во вкладке данные выберем команду Поиск решения. Назначим ячейку для целевой функции $D$3. Отметим, что целевая функция равна максимальному значению. Поместим курсор в строку Изменяя ячейки. Введем адреса искомых переменных $A$2:$C$2. Поместим указатель мыши на слово добавить. В окне Добавление ограничения в строке ссылка на ячейку введем адрес $D$4, в строке ограничения ввести $E$4. Введем остальные ограничения по данному алгоритму. Далее выберем параметры для решения задачи линейного программирования. Установим флажок в окне Линейная модель и Неотрицательные значения.

 

Рис. 3.3 - Поиск решения

 

Нажмем кнопку выполнить. Через некоторое время появится диалоговое окно результатов поиска и заполненные ячейки А2:С2, в ячейке D3 отобразится максимальное значение целевой функции.

Таблица 3.7

Решение задачи

 

х1	х2	х3
		3333,33
			333333,0
0,01	0,04	0,02	66,67
0,3			13333,33
1,5			16666,67
0,2	0,25	0,3

 

Z = 0*х₁ + 0*х₂ + 3333,33*x₃ = 333333,0 руб.

Ответ: Для получения максимального выхода продукции, составляющей 333333,0 руб. в условиях ограниченности ресурсов всю площадь лучше использовать под пашню.

Задания для самостоятельной работы студентов по решению задач симплексным методом представлены в приложении 3.