Пример выполнения расчетно-графической работы
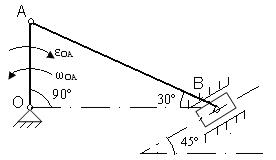
1. Исходные данные. Определить VA, VB, aA, aB, ω AB.
Дано: OA = 25см, АВ = 25см, ω OA = 2рад/с, ε OA = 4рад/с2

2. Решение
VA = ωOA· OA; VA = 50см/с; aA = ОА√ ω OA 4 + ε OA 2; aA = 140 см/с2. Для нахождения VB необходимо найти положение мгновенного центра скоростей (точку P) и воспользоваться VB= VABP/AP; ω AB= VA/AP. Для вычисления ускорения точки В необходимо воспользоваться теоремой о сложении ускорений, взяв точку А в качестве полюса.
Варианты заданий
КРИВОШИПНО-ШАТУННЫЙ МЕХАНИЗМ
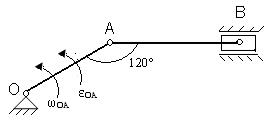
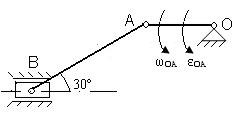
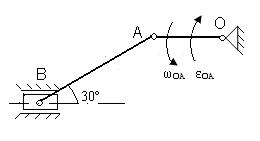
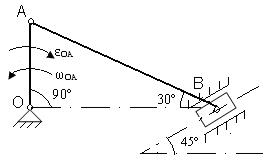
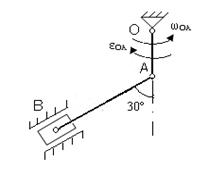
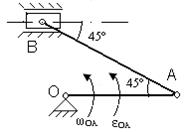
Для представленных на схемах механизмов, определить VA, VB, aA, aB, ωAB.
Исходные данные для расчета
| № вар. | Размеры, см | ω OA, рад/с | ε OA, рад/с2 | № вар. | Размеры, см | ω OA, рад/с | ε OA, рад/с2 | ||
| OA | AB | OA | AB | ||||||
1 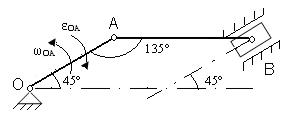
|

|

|

|

| 8 
|
|

|

|

|
|

|

|
|
|

|
|

|

|
|

| 26 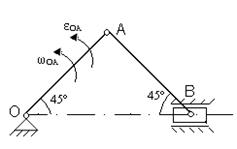
|

|
|

|

|

|

|

|

|
Сложное движение точки
Пример выполнения расчетно-графической работы
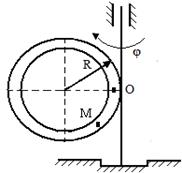
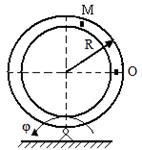
1. Исходные данные. ОМ(t) = t2 +t; φ (t) = t2 – t; R = 4м, t= 1c.


2. Решение. Определяем первоначально положение точки в заданный момент времени OM = 2м. Для нахождения абсолютной скорости необходимо найти относительную и переносную скорости:
Vот= ОМ(t)´= 2 t +1=3м/с; Vпер= ω∙ OM= φ (t) ´∙ OM=( 2 t- 1)∙ OM= 2м/с. Vабс=√V 2 от+V2пер-2Vот∙Vперcos β. Угол β - угол между вектором относительной скорости и вектором переносной скорости. cos β =OM/√R 2 +OM 2 = 2/√20=0,48. Тогда Vабс= 7,23м/с. Абсолютное ускорение находим согласно теореме Кориолиса.
Варианты заданий
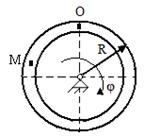
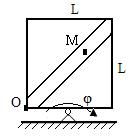
В приведенных схемах рассматривается движение точки М в желобе вращающегося тела. По заданным уравнениям относительного движения ОМ(t), переносного движения φ (t) и геометрическим размерам определить абсолютную скорость и абсолютное ускорение точки в указанный момент времени.
Исходные данные для расчета
| № вар. | ОМ(t), м | φ(t),рад | R или L,м | t,с |
| t 2 -t | 0,5 t 2 +t | |||
| 5π (t 2-3 ) | 3 t 2-8 t | |||
| t 3-4 t | 0,5 t 2 | |||
| 10π t 2 | 4 t 2-2 t | |||
| 2 t 2+2 t | 0,5 t 2 | |||
| 5π(2 t 2+ t) | 2 t 2 | |||
| 10π t 2 | 2 t 2- t | |||
| 3 t 2- t | t 2+3 t | |||
| 5π(t 2-2) | 2(t 2- t) | |||
| 8 t 2-2 t | 4 t 2 | 0,5 | ||
| 15π(t 2- t) | 6 t -4 t 2 | |||
| t 2+ t -1 | t 2 -t | |||
| 5π t 2 | t 2+ t | |||
| t 2 -t | 4 t - t 2 | |||
| 5π(2 t 2- t) | t 2+ t | |||
| t 2+ t | t 2- t | |||
| 5π t 2 | t 2+ t | |||
| t 2- t | 4 t - t 2 | |||
| 7π(2 t 2- t) | t 2+ t | |||
| 15π(t 2- t) | 6 t -4 t 2 | |||
| 8π t 2 | 2 t 2- t | |||
| 3 t 2 -t | t 2 + 3 t | |||
| 3π(t 2-2) | 2(t 2- t) | |||
| 8 t 2-2 t | 4 t 2 | |||
| 5π(2 t 2+ t) | 2 t 2 | |||
| 5π(t 2-3) | 3 t 2-8 t | |||
| t 3-4 t | 0,5 t 2 | |||
| 10π t 2 | 4 t 2-2 t | |||
| 2 t 2+2 t | 0,5 t 2 | |||
| t 2- t | 0,5 t 2+ t |

|

|

|

|

|

|

|

|
|
|

|

|

|

|

|
|

|

|

|

|

|

|

|

|

|

|

|

|
|

|
ДИНАМИКА
Основные понятия и определения
Таблица
Общие теоремы динамики
| Теорема об изменении количества движения |
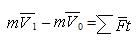
|
| Теорема об изменении кинетической энергии | mV 12/2 – mV 02/2 = ∑Ai=FS |
Таблица
Кинетическая энергия тела зависит от характера его движения.
| Поступательное движение | T = ½ mVc 2, Vc – скорость центра масс |
| Вращательное движение | T = ½ Jz ω2, Jz –момент инерции тела относительно оси вращения |
| Плоскопараллельное движение | T = ½ mVc 2 + ½ Jz ω2 |
Таблица
Момент инерции однородных тел
| Тело | Параметры тела | Ось | Момент инерции |
| Стержень | L – длина m- масса | Ось А -перпендикулярна стержню и проходит через его конец | JА =1/3mL2 |
| Тонкое круглое кольцо | R – радиус m - масса | Ось С - перпендикулярна плоскости кольца и проходит через его центр | JC = mR2 |
| Круглая пластина или цилиндр | R – радиус m- масса | Ось С - перпендикулярна плоскости пластины и проходит через его центр | JC =1/2mR2 |
| Сплошная прямоугольная пластина | m – масса А,В - стороны | Ось X – вдоль стороны А, ось Y – вдоль стороны В | JX =1/3mВ2 JY =1/3mА2 |
Принцип Даламбера. Основой для построения теоретической механики служат законы Ньютона. Однако на основе законов Ньютона можно получить некоторые другие общие законы, позволяющие составить уравнения, описывающие движение механической системы. Такие законы получили название принципов аналитической механики. Одним из них является принцип Даламбера. Пусть мы имеем систему, состоящих из n материальных точек. Выделим какую-нибудь из точек системы с массой 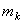 . Под действием приложенных к ней внешних и внутренних сил
. Под действием приложенных к ней внешних и внутренних сил  и
и 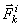 (в которые входят и активные силы, и реакции связи) точка получает по отношению к инерциальные системе отсчета некоторое ускорение
(в которые входят и активные силы, и реакции связи) точка получает по отношению к инерциальные системе отсчета некоторое ускорение  . Тогда оказывается, что движение точки обладает следующим общим свойством: если в каждый момент времени к фактически действующим на точку силам
. Тогда оказывается, что движение точки обладает следующим общим свойством: если в каждый момент времени к фактически действующим на точку силам  и
и 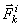 прибавить силу инерции
прибавить силу инерции  , то полученная система сил будет уравновешенной, т.е. будет
, то полученная система сил будет уравновешенной, т.е. будет  .
.
Это выражение отображает принцип Даламбера для одной материальной точки. Нетрудно убедиться, что оно эквивалентно второму закону Ньютона и наоборот. В самом деле, второй закон Ньютона для рассматриваемой точки дает  . Перенесем здесь член
. Перенесем здесь член  в правую часть равенства и придем к последнему соотношению. Принцип Даламбера для системы: если в любой момент времени к каждой из точек системы, кроме фактически действующих на ней внешних и внутренних сил, приложить соответствующие силы инерции, то полученная система сил будет находиться в равновесии и к ней можно будет применять все уравнения статики. Из статики известно, что геометрическая сумма сил, находящихся в равновесии, и сумма их моментов относительно любого центра О равны нулю, причём по принципу отвердевания это справедливо для сил, действующих не только на твёрдое тело, но и на любую изменяемую систему. Тогда на основании принципа Даламбера должно быть:
в правую часть равенства и придем к последнему соотношению. Принцип Даламбера для системы: если в любой момент времени к каждой из точек системы, кроме фактически действующих на ней внешних и внутренних сил, приложить соответствующие силы инерции, то полученная система сил будет находиться в равновесии и к ней можно будет применять все уравнения статики. Из статики известно, что геометрическая сумма сил, находящихся в равновесии, и сумма их моментов относительно любого центра О равны нулю, причём по принципу отвердевания это справедливо для сил, действующих не только на твёрдое тело, но и на любую изменяемую систему. Тогда на основании принципа Даламбера должно быть:
