1. Исходные данные.
Даны уравнения движения точки M:
X = 4t2 + 2, Y = 2t (где X,Y - в сантиметрах, t - в секундах).
Найти уравнение траектории точки M; для момента времени t1 = 1сек., найти положение точки на траектории, ее скорость, полное ускорение, касательное и нормальное ускорения, а также радиус кривизны в соответствующей точке.
2. Решение.
Из второго уравнения, подставляя значение t в первое уравнение, получим уравнение траектории X = Y2 + 2 – уравнение параболы.
Изобразим траекторию на координатной плоскости (рисунок).
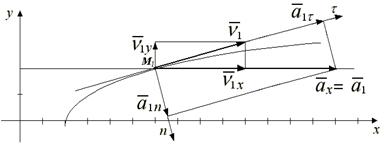
Найдем координаты, определяющие положение точки на траектории в момент времени t1=1сек.:X1=6см, Y=2см и точку обозначим М1.
Величину скорости точки М найдем по ее проекциям на координатные оси:
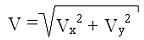
VX = (4t2 + 2)' = 8tсм/с, VY = (2t)' = 2см/с.
Тогда движение точки неравномерное. В момент времени t1=1сек.:V1X = 8см/с, V1Y = 2 см/с, V1 = 8,2 см/с.
Выберем масштаб и построим вектор скорости в положении М1 по составляющим V1X и V1Y.
Модуль ускорения точки Мопределяем аналогично

ax = 8см/с2, ay = 0
Полное ускорение a=ax=8см/с2 является постоянным.
Касательное ускорение определяется по формуле aτ = dV/dt.
Нормальное ускорение характеризует изменение скорости по направлению. В случае криволинейного движения, оно всегда существует и определяется по формуле an = V2/ρ, где ρ - радиус кривизны траектории в соответствующей точке. Т.к. радиус кривизны параболы в точке М 1 неизвестен, то величину нормального ускорения можно определить следующим образом:
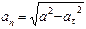
Радиус кривизны параболы в точке М1 найдем из выражения
ρ1 = V21/a1n = 68/1,8 = 37,8см
Ответ: точка М совершает криволинейное ускоренное движение, т.к. вектор касательного ускорения во все время движения совпадает с направлением вектора скорости.
Варианты заданий
Точка М движется в плоскости xOy согласно уравнениям: x=x(t), y=y(t).
Определить траекторию движения точки, для заданного момента времени t найти положение точки на траектории, ее скорость и ускорение и показать их на рисунке, а также определить радиус кривизны траектории в данной точке.
Таблица
Исходные данные для расчета
| № вар | X, см | Y, см | t, с | № вар | X, см | Y, см | t, с |
| 4t2 + 3t + 7 | 8t2 + 6t + 1 | t2 + 4t + 3 | t2 + 8t + 1 | ||||
| 3t2 + 6t + 2 | 3t | -t - 1 | -2/(t + 1) | ||||
| 3cos(πt/3) | 5sin(πt/3) | t2 | 3t - 2 | ||||
| 3/(t+1) | 3t+3 | 2sin(πt/8)+2 | 2cos(πt/8)-1 | ||||
| 2sin(πt/3) +1 | 3cos(πt/3) | 2t3 + 3 | 6t3 + 12 | ||||
| 3t2 + 2t + 5 | 9t2 + 6t + 11 | -3/(t + 1) | -3t - 3 | ||||
| 2t2 + 6t + 2 | 2t | t4 + 1 | t4 - 2 | ||||
| t2 - 4t + 1 | t + 1 | 3cos(t) | 3sin(t) | π/6 | |||
| -4/(t + 1) | -2t - 2 | 10/(5t + 1) | 2,5t | ||||
| 2t2 + 4 | 3t + 1 | 2cos(πt/6) | 3sin(πt/6)+3 | ||||
| 3sin(πt/4) +2 | 4cos(πt/4)- 1 | 3cos(πt/3)+2 | 3sin(πt/3)-2 | ||||
| 7t + 1 | -8/(7t + 1) | 3t2 + 3t + 3 | 8t2 + 8t + 5 | ||||
| 3cos(πt/6)+1 | 2sin(πt/6) -2 | t2 + 6t + 2 | 2t | ||||
| 4t + 5 | 5t2 + 1 | 5/(t+1) | 5t+5 | ||||
| 4cos(πt/4) | 4sin(πt/4)- 1 | 2cos(πt/3) | 3sin(πt/3)+2 |
Простейшие виды движения твердого тела
Пример выполнения расчетно-графической работы
1. Исходные данные.
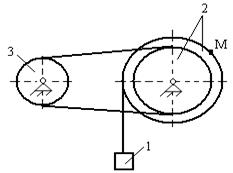
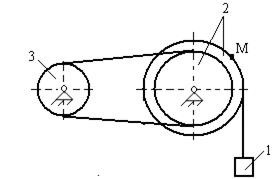
Определить скорость и ускорение точки М, а также скорость и ускорение груза 1 в заданный момент времени.
Дано: x(t) = 7t2, R2 = 25см, r2 = 15см, R3 = 20см, r3 = 10см, t1 = 1c

2. Решение
V1 = x´(t) = 14t; a1 = 14м/с2;
V1(t1) = 14м/с
VМ = V1(r2· r3)/(R2· R3); VМ =4,2t;
VM(t1) = 4,2м/с
aM = √aτ2 + an2;
aτ = VМ´ = 4,2м/с2; an = VМ2/ r3 = 1,76 м/с2;
aM =4,55 м/с2
Тогда
| V 1 | a 1 | VМ | aM |
| 14м/с | 14м/с2 | 4,2м/с | 4,55 м/с2 |
Варианты заданий
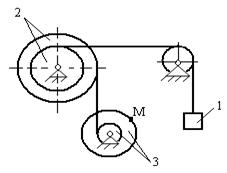
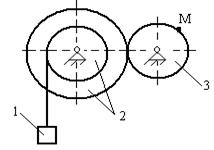
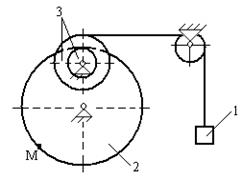
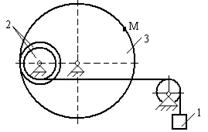
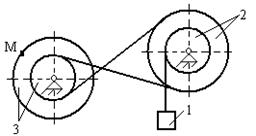
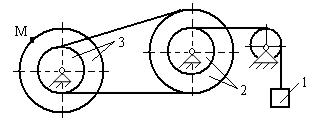
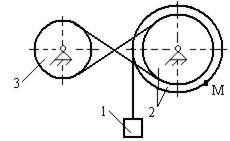
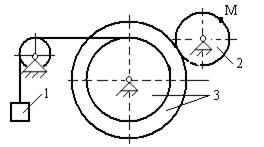
Для приведенных схем механизмов по известным характеристикам движения определить и показать на рисунке скорость и ускорение точки М, а также скорость и ускорение груза 1 в заданный момент времени. Исходные данные приведены в таблице. Обозначения: V1 - скорость тела 1, a1 - ускорение тела 1, x(t) - уравнение движения тела 1, φ3(t) - уравнение движения тела 3, R2, r2, R3, r3 - радиусы шестерен, шкивов и барабанов.
Исходные данные для расчета
Исходные данные для расчета
| № вар. | Характеристики движения | Радиусы, см | Время, с | |||
| R 2 | r 2 | R 3 | r 3 | |||
| V 1=0,5м/с, a 1=-0,7м/с2 | - | - | ||||
| x(t)= 5 t 2 м | 0,5 | |||||
| φ3(t)=0,5 t 3-2 t 2 рад | - | |||||
| φ3(t)= t -2e0.5 t рад | - | |||||
| φ3 (t)=t 3-7 t рад | - | |||||
| φ3(t) =3 t 2+5 рад | - | 0,25 | ||||
| V 1=0,25м/с, a 1=0,6м/с2 | - | - | ||||
| x(t)= 42 t -0,6 t 3 м | ||||||
| V 1=-0,5м/с, a 1=1,0м/с2 | - | - | ||||
| x(t)= 22 t- 5 t 2 м | ||||||
| V 1=1,0м/с, a 1=2,0 м/с2 | - | - | ||||
| x(t)= 42 t -5 t 2 м | ||||||
| V 1=-1,5м/с, a 1=4,5м/с2 | - | - | ||||
| φ3(t)=5(1- cos (π t /6)) рад | - | |||||
| V 1=0,4м/с, a 1= 0,4 м/с2 | - | - | ||||
| φ3(t)=4 t -0,5 t 2 рад | - | |||||
| V 1=0,6м/с, a 1= -0,9 м/с2 | - | - | ||||
| φ3 (t)= 8 sin (π t /3) рад | - | |||||
| x(t)= 5 t -0,5 t 3 м | ||||||
| V 1=0,8м/с, a 1= 12,8 м/с2 | - | - | ||||
| x(t)= 5 t- 15 sin (π t /6) м | ||||||
| x(t)= 0,5(1- cos (π t)) м | 1/6 | |||||
| φ3(t)= t 2-2e t рад | - | 0,5 | ||||
| V 1 =- 1,5 м/с, a 1=4,5 м/с2 | - | - | ||||
| V 1=0,5м/с, a 1= -0,9 м/с2 | - | - | ||||
| φ3 (t)=10 t -2 t 2 рад | - | |||||
| φ3 (t)=5(1- cos (π t /6)) рад | - | 1,5 | ||||
| V 1=0,25 м/с, a 1=0,7м/с2 | - | - | ||||
| φ3(t)=0,5 t 3-2 t 2 рад | - | 1,5 | ||||
| φ3(t)=3 t 2+5 рад | - | 0,35 |

|

|

|

|
|
|

|
|

|

|

|

|

|
|

|

|

|

|
|

|
|

|
|
|

|

|
|
|

|

|