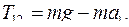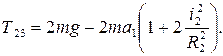Динамика механических систем с одной степенью свободы

Пример выполнения расчетно-графической работы

1.Теорема об изменении кинетической энергии

 

 

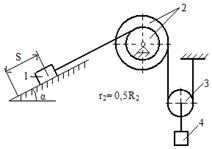
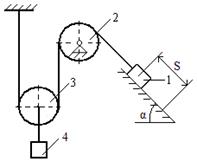
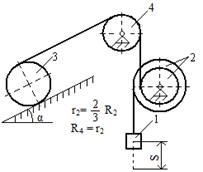
Дано: m₁=m; m₂=2m; m₃=m; R₂=2r₂; 2R₃=r₂; i ₂; δ; S₁; α.

Найти: ; .

Решение:

1. Теорема об изменении кинетической энергии.

 

 

2. Кинематика системы.

V₁;

1 тело – поступательное движение;

2 тело – вращательное движение;

3 тело – плоскопараллельное движение.

3. Моменты инерции тел.

 

;

.

 

4. Кинетическая энергия тел и системы.

Т = Т ₁ + Т ₂ + Т ₃ .

;

;

;

.

 

5. Работа внешних сил.

.

, (т.к. h₁ = S₁);

;

;.

.

6. Используя теорему, находим искомые величины

;

 

7. V₁ = f ₁(t); S₁= f ₂(t);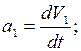

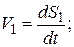
, т.к. а

 

 

или

 

2. Теорема об изменении кинетического момента

Дано: m₁=m; m₂=2m; m₃=m; R₂=2r₂; 2R₃=r₂; i ₂; δ; α.

Найти: .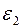

Решение:

 

1. Теорема об изменении кинетического момента

. .

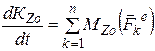2. Кинематика системы.

т.к. R ₂ = 4 R ₃, r ₂ = 2 R _3.

3. Моменты инерции тел.

;

.

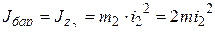4. Моменты количества движения тел и системы.

, т.к. V ₁ = ω ₂ · R ₂.

.

, т.к. ω₃ = ω₂.

.

 

5. Момент сил относительно т. О.

тело 1. ;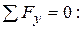

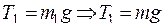тело 3. ;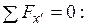

тело 2. .

6. Находим искомую величину, используя теорему об изменении кинетического момента.

т.к. .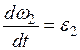

Следовательно:

3. Принцип Даламбера при исследовании механических систем

 

Дано: m₁=m; m₂=2m; m₃=m; R₂=2r₂; 2R₃=r₂; i ₂; δ; α.

Найти:

Решение:

1. Ускорения точек тел и тел системы

2. Главные векторы и главные моменты сил инерции

 

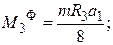
3. Принципы Даламбера для тела 1.

.

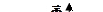
Уравнение равновесия

 

.

 

4. Принципы Даламбера для тела 2.

 

Уравнение равновесия

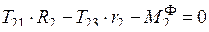Т ₂₁ = Т ₁₂

(r ₂ = 0,5 R ₂)

.

 

.

5. Принципы Даламбера для тела 3.

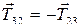Т ₃₂ = Т ₂₃

 

Уравнение равновесия

;

 

 

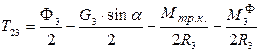Умножим уравнение на

.

Сгруппируем слагаемые

.

Откуда .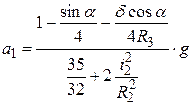

4. Исследование механической системы с помощью общего уравнения динамики

Дано: m₁=m; m₂=2m; m₃=m; R₂=2r₂; 2R₃=r₂; i ₂; δ; α.

Найти: .

 

Решение:

1. Конечные перемещения точек и тел системы

δS₁; .

 

2. Ускорения точек тел и тел системы.

a ₁; .

3. Главные векторы и главные моменты сил инерции.

; ; ;

; ; ;

;

.

 

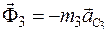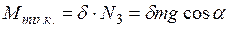4. Общее уравнение динамики системы.

;

 

;

 

 

.

 

 

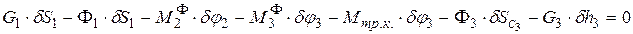
5. Общее уравнение динамики для тела 1.

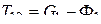
6. Общее уравнение динамики для тела 2.

;

 

(по условию );

 

;

;

;

(3)

Варианты заданий

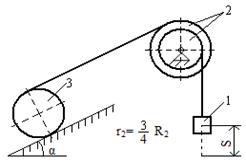
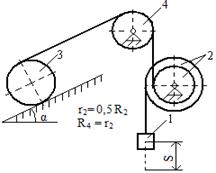
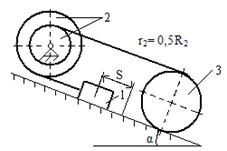
Механическая система под действием силы тяжести приходит в движение из состояния покоя. Начальное положение системы показано на схемах. Учитывая трение скольжения тела 1 и сопротивление качению тела 3, определить ускорение тела 1 в тот момент времени, когда пройденный им путь станет равным S. Задачу можно решить одним из трех способов: используя теорему об изменении кинетической энергии, используя принцип Даламбера или используя общее уравнение динамики.

Таблица

Исходные данные для расчета

№ вар.	m 1	m 2	m 3	m 4	R 2	R 3	i 2	i 3	α	β	f	δ, см
кг	см	град
	m	m	1/9 m	m	-	-	-	-		-	0,10	-
	m	1/4 m	1/4 m	1/5 m	-	-	-	-		-	0,10	-
	m	1/2 m	1/3 m	-	-		-				0,22	0,20
	m	1/3 m	1/4 m	-	-		-				0,20	0,10
	m	1/4 m	m	1/9 m	-	-	-	-		-	0,10	-
	m	4 m	1/5 m	4/3 m	-	-	-	-		-	0,10	-
	m	1/3 m	1/4 m	1/9 m	-	-	-	-		-	0,20	-
	m	1/3 m	1/9 m	-	-		-				0,15	0,24
	m	2 m	m	0,5 m	-		-				0,12	0,10
	m	3 m	m	-	-		-	-			0,10	0,28
	m	1/3 m	1/9 m	1/5 m	-	-	-	-		-	0,15	-
	m	5 m	4 m	-	-		-	-			0,26	0,15
	m	4 m	1/5 m	4/5 m	-	-	-	-		-	0,20	-
	m	1/2 m	1/4 m	1/3 m	-	-	-	-		-	0,10	-
	m	4 m	3 m	-	-		-	-			0,10	0,25
	m	1/4 m	1/8 m	m	-		-	-			0,20	0,20
	m	1/2 m	1/4 m	-	-		-				0,17	0,15
	m	1/3 m	1/4 m	1/8 m	-	-	-	-		-	0,25	-
	m	2 m	2 m	-				-		-	-	0,20
	m	1/2 m	1/3 m	-	-		-	-			0,15	0,20
	m	3 m	2 m	-	-		-	-			0,10	0,20
	m	1/4 m	1/5 m	m	-		-	-			0,25	0,20
	m	1/3 m	1/5 m	-	-		-				0,20	0,10
	m	2 m	3 m	-				-		-	-	0,25
	m	3 m	1/5 m	4/5 m	-	-	-	-		-	0,25	-
	m	1/2 m	1/5 m	1/3 m	-	-	-	-		-	0,15	-
	m	1/2 m	1/3 m	-	-		-				0,15	0,20
	m	1/3 m	1/4 m	1/8 m	-	-	-	-		-	0,15	-
	m	2 m	1,5 m	0,5 m	-		-				0,2	0,10
	m	1/4 m	1/4 m	1/4 m	-	-	-	-		-	0,10	-

15
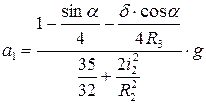