Практическое вычисление пределов основывается на свойствах пределов, описанных в теоретической части.
Задача 1. Найти  .
.
 Основываясь на свойствах пределов (предел суммы и произведения), имеем
Основываясь на свойствах пределов (предел суммы и произведения), имеем
 .
.
 |
Напомним, что элементарные функции непрерывны в своей области определения, а значит, предел функции в точке области определения равен значению функции в этой точке. Поэтому для того чтобы найти предел элементарной функции, когда аргумент стремится к значению, принадлежащему области определения этой функции, нужно в выражение функции вместо аргумента подставить его предельное значение. Тогда вычисление последнего предела можно оформить так:  .
.
Кроме того, при вычислении пределов необходимо помнить и о свойствах бесконечно малых и бесконечно больших функций.
 Задача 2. Найти
Задача 2. Найти 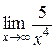 .
.
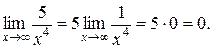
 Поскольку знаменатель дроби
Поскольку знаменатель дроби  при
при  является бесконечно большой величиной, то обратная величина
является бесконечно большой величиной, то обратная величина  есть бесконечно малая, а значит,
есть бесконечно малая, а значит,  .
.
Однако не всегда подстановка предельного значения аргумента в функцию позволяет сразу получить результат. Часто возникают неопределенности различных видов:  .
.
Рассмотрим задания, связанные с раскрытием различных видов неопределенностей.
1. Неопределенность 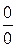
Говорят, что выражение  представляет неопределенность вида
представляет неопределенность вида 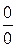 при
при  , если
, если  . Раскрыть эту неопределенность – значит, найти
. Раскрыть эту неопределенность – значит, найти  . Приведем основные методы раскрытия такой неопределенности.
. Приведем основные методы раскрытия такой неопределенности.
а) Разложение многочленов, присутствующих в числителе и знаменателе дроби, на множители
Задача 3. Найти  .
.
 При подстановке предельного значения
При подстановке предельного значения  в функцию убеждаемся, что имеем неопределенность вида
в функцию убеждаемся, что имеем неопределенность вида 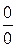 .
.
Разложим числитель и знаменатель на множители. Поскольку в числителе присутствует квадратный трехчлен, то для его разложения найдем корни ( ). В знаменателе используем формулу сокращенного умножения – сумму кубов. Получим:
). В знаменателе используем формулу сокращенного умножения – сумму кубов. Получим:
 .
.

б) Перевод иррациональности из знаменателя в числитель и наоборот
При вычислении пределов, содержащих иррациональные выражения, для снятия неопределенности вида 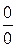 применяется перевод иррациональности из знаменателя в числитель и, наоборот, путем домножения числителя и знаменателя дроби на выражение, сопряженное к имеющемуся в дроби иррациональному выражению.
применяется перевод иррациональности из знаменателя в числитель и, наоборот, путем домножения числителя и знаменателя дроби на выражение, сопряженное к имеющемуся в дроби иррациональному выражению.
Задача 4. Найти  .
.
 Имеем неопределенность
Имеем неопределенность 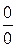 . Домножим числитель и знаменатель дроби на выражение
. Домножим числитель и знаменатель дроби на выражение 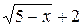 , являющееся сопряженным к числителю исходной дроби. Получим:
, являющееся сопряженным к числителю исходной дроби. Получим:

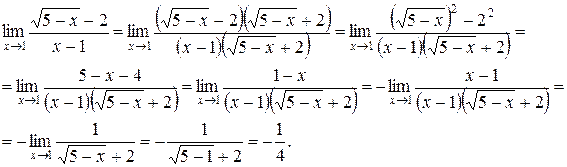
в) Применение первого замечательного предела
При вычислении некоторых пределов, содержащих тригонометрические функции можно использовать первый замечательный предел:
 .
.
Задача 5. Найти  .
.

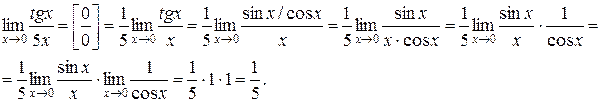
 Предел
Предел  вычислили непосредственной подстановкой предельного значения аргумента в функцию.
вычислили непосредственной подстановкой предельного значения аргумента в функцию.
г) Применение таблицы эквивалентности
Данный метод основан на том, что предел отношения двух бесконечно малых функций не изменится, если эти бесконечно малые заменить им эквивалентными.
Таблица эквивалентности (при  )
)

Задача 6. Найти  .
.
 Имеем неопределенность вида
Имеем неопределенность вида 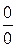 . Поскольку
. Поскольку  при
при  , то
, то  , т.е. является бесконечно малой функцией, а значит, на основании таблицы эквивалентности
, т.е. является бесконечно малой функцией, а значит, на основании таблицы эквивалентности 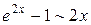 .
.
Получаем:

 .
.
Задача 7. Найти  .
.

 .
.
 Т.е. поскольку
Т.е. поскольку 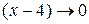 при
при  , то
, то  , а значит,
, а значит,  .
.
2. Неопределенность 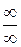
Говорят, что выражение  представляет неопределенность вида
представляет неопределенность вида 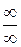 при
при  , если
, если  . Раскрыть эту неопределенность – значит найти
. Раскрыть эту неопределенность – значит найти  .
.
Примером такой неопределенности является дробно-рациональная функция  , где
, где 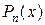 и
и  – многочлены с действительными коэффициентами степени
– многочлены с действительными коэффициентами степени 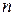 и
и  соответственно. Для раскрытия такой неопределенности необходимо числитель и знаменатель дроби разделить на старшую из степеней многочленов
соответственно. Для раскрытия такой неопределенности необходимо числитель и знаменатель дроби разделить на старшую из степеней многочленов  и
и  , а затем использовать теоремы о пределах.
, а затем использовать теоремы о пределах.
Задача 8. Найти  .
.
 Разделим числитель и знаменатель дроби на
Разделим числитель и знаменатель дроби на  (как старшую из степеней числителя и знаменателя), получим:
(как старшую из степеней числителя и знаменателя), получим:
 .
.
 При этом использовали свойства пределов (предел дроби, суммы, вынесение константы за знак предела), а также, что функции
При этом использовали свойства пределов (предел дроби, суммы, вынесение константы за знак предела), а также, что функции 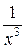 и
и 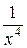 бесконечно малые при
бесконечно малые при  , а значит,
, а значит,  .
.
Вообще, используя этот прием можно показать, что справедливо следующее правило:

Задача 9. Найти  .
.
 Разделим числитель и знаменатель дроби на
Разделим числитель и знаменатель дроби на 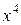 :
:

 ,
,
поскольку обратная к бесконечно малой величине есть бесконечно большая.
3. Неопределенность 
Говорят, что выражение  представляет неопределенность вида
представляет неопределенность вида 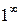 при
при  , если
, если 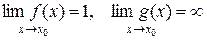 .
.
При раскрытии такой неопределенности используется второй замечательный предел: 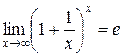 или
или  .
.
Задача 10. Найти  .
.


 .
.
Задача 11. Найти  .
.



Задача 12. Найти  .
.



4. Неопределенности 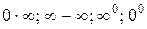
Неопределенности 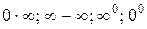 алгебраическими преобразованиями сводятся к уже рассмотренным выше неопределенностям.
алгебраическими преобразованиями сводятся к уже рассмотренным выше неопределенностям.
Задача 13. Найти 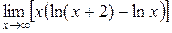 .
.
 Используя свойства логарифма, выполним преобразования под знаком предела:
Используя свойства логарифма, выполним преобразования под знаком предела:

На основании непрерывности логарифмической функции перейдем к пределу под символом логарифма:

 |
 Задача 14. Найти
Задача 14. Найти  .
.
В данном случае, чтобы раскрыть неопределенность  , необходимо умножить и разделить рассматриваемое выражение на «сопряженное», чтобы прийти к разности квадратов. Таким образом, получаем:
, необходимо умножить и разделить рассматриваемое выражение на «сопряженное», чтобы прийти к разности квадратов. Таким образом, получаем:

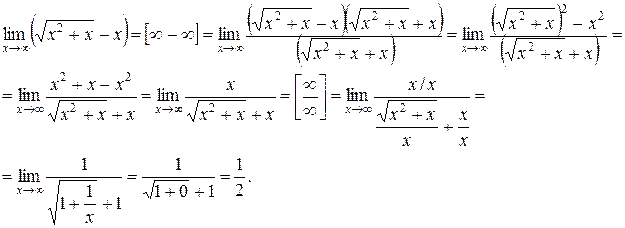 Итак,
Итак, 