Производная функции
Таблица производных основных элементарных функций
1.  , с =const.
, с =const.
2.  , где
, где 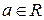 . В частности,
. В частности, 
3. 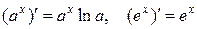 .
. 
4. 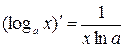 ,
,  .
. 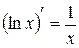 .
.
5. 
6. 
7. 
8. 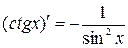
9. 
10. 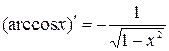
11. 
12. 
Правила дифференцирования
Пусть  , с - const.
, с - const.
1. 
2. 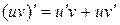 . В частности,
. В частности,  .
.
3. 
4. (Сложная функция). 
Задача 1. Найти производные функций:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
 е)
е) 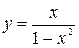 .
.
а) 

 ;
;
б) 
 ;
;
в) 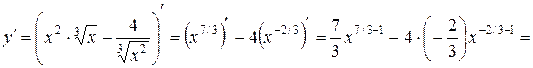
 ;
;
г)  ;
;
д) 

 ;
;
 е)
е)  .
.
Задача 2. Найти производные функций:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
е)  .
.
 Данные функции являются сложными, поэтому при их дифференцировании применим правило дифференцирования сложной функции.
Данные функции являются сложными, поэтому при их дифференцировании применим правило дифференцирования сложной функции.
а)  ;
;
б)  ;
;
в)  ;
;
г) 
 ;
;
д) 
 ;
;
е)

 |
Логарифмическое дифференцирование
Логарифмическое дифференцирование применяется для дифференцирования степенно-показательной функции, т.е. функции вида  , а также дробно-рациональных функций.
, а также дробно-рациональных функций.
 Задача 3. Найти производную функции
Задача 3. Найти производную функции 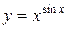 .
.
1) прологарифмируем обе части равенства:

 ;
;
2) продифференцируем обе части, учитывая, что  :
:

 ;
;
3) выразим  :
:

 ;
;
4) подставим  :
:

 Итак,
Итак, 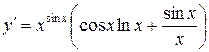 .
.
Дифференцирование неявной функции
 Задача 4. Найти производную
Задача 4. Найти производную  функции
функции  .
.
1) Продифференцируем обе части равенства, учитывая, что  :
:
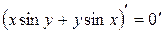



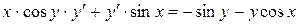
 .
.
2) Выразим  :
:


Задача 5. Найти производную второго порядка функции  .
.



 .
.
Задача 6. Найти производную функции  в точке x=2.
в точке x=2.
 Функция представляет собой частное, поэтому применяем правило дифференцирования дроби, а также формулу производной степенной функции (для
Функция представляет собой частное, поэтому применяем правило дифференцирования дроби, а также формулу производной степенной функции (для  и для
и для  ):
):

Вычисляем производную в заданной точке, для этого подставляем в найденное выражение значение x=2:

 =
= 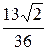 .
.
Задача 7. Найти дифференциал функции  .
.
 |
Используем формулу дифференциала функции одной переменной:
 .
.

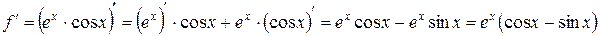 тогда
тогда  .
.
Дифференцирование функций, заданных
параметрически
Пусть функция задана параметрическими уравнениями  ,
,
тогда 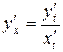 , или
, или 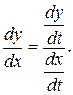
Задача 8. Найти  , если
, если




Правило Лопиталя
Если при вычислении пределов затруднительно использование эквивалентностей, то можно применить следующее утверждение.
Правило Лопиталя. Пусть функции f(x) и g(x) определены и дифференцируемы в окрестности точки a, а также являются одновременно бесконечно малыми (или бесконечно большими) при 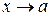 . Пусть, далее,
. Пусть, далее,  в окрестности точки a (кроме, возможно, самой точки). Если существует
в окрестности точки a (кроме, возможно, самой точки). Если существует 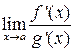 , то существует и
, то существует и 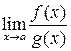 , причем
, причем  .
.
Задача. Найти с помощью правила Лопиталя:
 а)
а)  ; б)
; б) 
a)В данном случае после подстановки x= 0 замечаем, что и числитель, и знаменатель дроби обращаются в нуль, т.е. мы имеем дело с неопределенностью  . Однако использовать замечательные пределы и перейти к эквивалентным функциям нельзя, так как в числителе – сумма функций. Воспользуемся правилом Лопиталя, предварительно проверив все его условия.
. Однако использовать замечательные пределы и перейти к эквивалентным функциям нельзя, так как в числителе – сумма функций. Воспользуемся правилом Лопиталя, предварительно проверив все его условия.
Неопределенность  уже отмечена. Функции, стоящие в числителе и знаменателе, дифференцируемы при всех действительных x и
уже отмечена. Функции, стоящие в числителе и знаменателе, дифференцируемы при всех действительных x и  при
при  . В силу сформулированного выше утверждения, если в этом случае существует предел отношения производных, то его значение совпадет со значением искомого предела. Предположим, что это так, и проведем вычисления:
. В силу сформулированного выше утверждения, если в этом случае существует предел отношения производных, то его значение совпадет со значением искомого предела. Предположим, что это так, и проведем вычисления:

Итак, 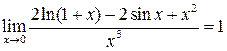
При решении этого примера правило Лопиталя фактически было применено трижды (в тех местах, где над знаком равенства указан вид неопределенности). При этом для обеспечения строгости рассуждений необходимо каждый раз проверять условия правила Лопиталя.
Рассмотрим теперь задание б). Очевидно, что здесь вообще нет эквивалентных функций. Кроме того, при 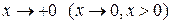
 и
и  . Это неопределенность вида
. Это неопределенность вида  , к которой правило Лопиталя не применяется, однако можно учесть, что если f(x) – бесконечно малая при
, к которой правило Лопиталя не применяется, однако можно учесть, что если f(x) – бесконечно малая при 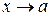 функция, то
функция, то 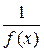 будет бесконечно большой при
будет бесконечно большой при 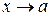 . Таким образом, поскольку
. Таким образом, поскольку
 ,
,
мы приходим к неопределенности  и далее действуем так, как при решении задания а). Обе функции требуемым условиям удовлетворяют, поэтому
и далее действуем так, как при решении задания а). Обе функции требуемым условиям удовлетворяют, поэтому

 (учтено, что
(учтено, что  ). Итак,
). Итак,  .
.