1. Экстремумы функции. Интервалы монотонности функции.
План нахождения локального экстремума
1. Найти критические точки функции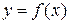 
, для чего решить уравнение 
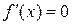, а также найти точки, где 
не существует.
2. Полученными точками разбить числовую ось на интервалы.
3. В каждом интервале определить знак производной 
и применить достаточное условие экстремума функции одной переменной: Если меняет свой знак при переходе через критическую точку, то в ней локальный экстремум (минимум, если знак меняется с «-» на «+», максимум – иначе), иначе экстремума в рассматриваемой критической точке нет.
Задача 1. Найти интервалы возрастания и убывания функции, экстремумы функции 
.
.
Для нахождения критических точек решим уравнение:
.
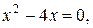
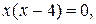
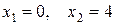Точек, в которых производная не определена нет, т.к. 
определена при любых х.
Далее отметим найденные точки на числовой оси и определим знаки производной в получившихся промежутках:
 |
+ – +
0 4
На основании достаточного условия экстремума функции одной переменной заключаем: х =0 – точка максимума, х =4 – точка минимума.
.
Таким образом, экстремумами функции являются значения: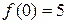 
– максимум, 
– минимум.
Интервалы возрастания функции: 
, убывания: 
.
 |
2. Нахождение наибольшего и наименьшего значения функции 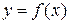на отрезке [a,b].
План нахождения наибольшего и наименьшего значений функции на отрезке
1. Найти критические точки функции 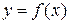на отрезке [a,b].
2. Вычислить значения функции 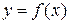в критических точках и на концах отрезка.
3. Выбрать из полученных значений наибольшее (наименьшее).
Задача 2. Найти наименьшее и наибольшее значение функции на отрезке 
на отрезке [-3;2].
1) найдем критические точки функции:
, 
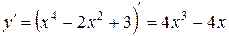или
, тогда
.
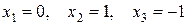Отметим, что все три точки лежат в указанном отрезке [-3;2].
2) Вычислим значения функции в критических точках и на концах отрезка:
3) Из найденных значений функции выбираем наибольшее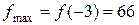 
и наименьшее 
.
3. Интервалы выпуклости, вогнутости. Точки перегиба.
План нахождения точек перегиба функции
1. Найти 
.
2. Найти корни уравнения 
, а также точки, в которых 
не существует.
3. Полученными точками 
разбить числовую ось на интервалы.
4. Определить знак в этих интервалах. Если в рассматриваемом интервале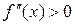 
, то здесь кривая 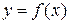вогнута, а если 
, то выпукла. Если при переходе через меняет свой знак, то эта точка является точкой перегиба.
Задача 3. Найти точки перегиба и промежутки выпуклости и вогнутости функции 
.
,
при 
.
При х =5 производная 
не существует.
На числовой оси отметим лишь точку х =5, и определим знаки в полученных интервалах:
– +
Поскольку при переходе через точку х =5 вторая производная меняет свой знак, то х =5 – точка перегиба, 
.
На промежутке 
функция выпукла, на промежутке 
– вогнута.
4. Асимтоты.
1) Вертикальная асимптота.
Прямая х=а является вертикальной асимптотой для функции 
, если выполняется одно из условий 
! Непрерывные функции на своей области определения не имеют вертикальных асимптот.
2) Наклонная асимптота.
Для наклонная асимптота у = kx + b находится по формулам:
. Если k =0, то наклонная превращается в горизонтальную асимптоту у = b.
Задача 4. Найти асимптоты графика функции 
.
Область определения функции: 
.
Прямая 
является вертикальной асимптотой, т.к. 
.
Найдем наклонную асимптоту: 
;
.
Итак, 
- наклонная асимптота, – вертикальная асимптота.
5. Построение графиков функций.
План исследования функции и построения ее графика
1. Найти область определения функции.
2. Исследовать функцию на четность, нечетность, периодичность. В случае, когда, например, функция является нечетной (четной), достаточно проводить исследования и строить эскиз графика при 
с последующим симметричным его отображением (относительно начала координат для нечетной функции или относительно оси OY для четной).
3. Определить координаты точек пересечения графика функции с осями координат (для нахождения точки пересечения графика с осью OX решаем уравнение f(x)= 0; для нахождения точки пересечения графика с осью OY подставляем в аналитическое выражение функции значение x= 0).
4. Определить промежутки знакопостоянства функции (т.е. промежутки, где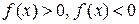 
).
5. Определить асимптоты графика функции.
6. Определить интервалы монотонности функции, экстремумы функции.
7. Определить интервалы выпуклости и вогнутости графика функции, найти точки перегиба.
8. Построить эскиз графика.
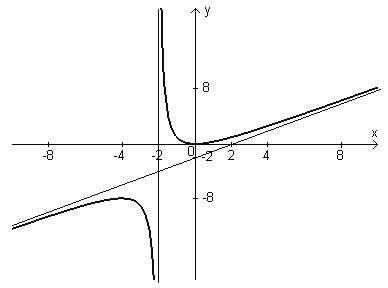
Задача 5. Провести полное исследование и построить график функции 
.
Придерживаемся предложенной схемы исследования.
1. Функция определена при всех действительных x, кроме x = -2.
2. Исследуем функцию на четность (нечетность):
, кроме того, 
.
Таким образом, функция не является ни четной, ни нечетной, т.е. имеем функцию общего вида. Функция не является периодической.
3. Решая уравнение f(x)= 0, находим, что график функции пересекает оси координат в точке ( 0, 0 ).
4. Определим промежутки знакопостоянства функции. Для этого на числовой оси отметим нули функции, т.е. точки пересечения с осью Ох, и точки, в которых функция не определена. А далее определим знаки функции в получившихся промежутках:
– + +
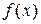-2 0
Таким образом, функция положительна (а значит ее график расположен над осью Ох) на промежутке 
; функция отрицательна (а значит ее график расположен под осью Ох) на промежутке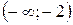 
.
5. В силу свойств непрерывных функций функция 
непрерывна там, где определена, т.е. при всех действительных x, кроме
x=- 2. Поэтому, поскольку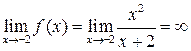 
, то прямая x = - 2является вертикальной асимптотой графика.
Найдем теперь уравнение наклонной асимптоты:
.
Таким образом, прямая 
– наклонная асимптота.
6. Для определения экстремумов функции найдем первую производную: 
,
и решим уравнение: 
, т.е. 
.
Откуда получаем критические точки: 
.
+ – – +
-4 -2 0
Таким образом, x = - 4 – точка максимума, x = 0– точка минимума. Экстремумы функции: 
.
Кроме того, f(x) возрастает на интервалах 
и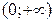 
, а убывает на интервалах 
и 
.
7. Найдем теперь вторую производную:
Очевидно, что знак второй производной зависит только от знака знаменателя. При x>- 2 
и график направлен выпуклостью вниз, а при x>- 2 
и график направлен выпуклостью вверх.
Используя полученную информацию о функции, строим эскиз графика.
