ВЫЧИСЛЕНИЕ КЛАССИЧЕСКОЙ ВЕРОЯТНОСТИ

МИНЕСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

 

Государственное образовательное учреждение высшего профессионального образования

ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

Филиал ВЗФИ в г. Барнауле

Региональная кафедра Математики и информатики

 

Г.В. Черняев

 

Теория вероятностей. Часть 1.

Методические указания к решению задач по теории вероятностей

 

 

Барнаул - 2009

УДК 51

ББК 22.143+22.161

 

Черняев Г. В. Теория вероятностей. Часть 1: Методические указания к решению задач по дисциплине “Теория вероятностей и математическая статистика” / Филиал ВЗФЭИ в г. Барнауле

 

 

Методические указания предназначены для самостоятельной работы студентов 2-го курса всех специальностей, бакалавров и слушателей ФНО по дисциплине «Теория вероятностей и математическая статистика».

 

 

Печатается по решению региональной кафедры математики и информатики филиала ВЗФЭИ в г. Барнауле (протокол № 11 от 19.06. 2009г.)

Рецензент - Свердлова Е.Г., к.ф.-м.н., доцент кафедры математики и информатики филиала ВЗФЭИ в г. Барнауле.

 

 

 

 

 

ОГЛАВЛЕНИЕ

 

ПРЕДИСЛОВИЕ

1. СЛУЧАЙНОЕ СОБЫТИЕ

2. ВЫЧИСЛЕНИЕ КЛАССИЧЕСКОЙ ВЕРОЯТНОСТИ

3. ВЫЧИСЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ВЕРОЯТНОСТЕЙ

4. ВЕРОЯТНОСТИ СЛОЖНЫХ СОБЫТИЙ

5. ФОРМУЛЫПОЛНОЙ ВЕРОЯТНОСТИ И БАЙЕСА

6. ФОРМУЛА БЕРНУЛЛИ

7. ФОРМУЛЫПУАССОНА И МУАВРА-ЛАПЛАСА

8. ОТВЕТЫ

 

 

ПРЕДИСЛОВИЕ

Цель пособия - помочь студентам приобрести навыки применения вероятностно-статистических методов к решению различных задач. Поэтому при подборе задач и методов их решения основное внимание было обращено не на формально-математическую сторону, а на их прикладное содержание.

Учебное пособие состоит из 7 разделов. В начале каждого раздела приведена краткая сводка теоретических сведений и формул, необходимых для решения задач этого раздела; затем даны решения типовых задач и задачи для самостоятельного решения. Все задачи снабжены ответами. Задачи, имеющиеся в пособии, различны по трудности. Среди них есть как задачи для простого приобретения навыков применения готовых формул и теорем, так и более сложные задачи, решение которых требует некоторой изобретательности.

При отборе задач были использованы источники, список которых приведен в конце пособия.

СЛУЧАЙНОЕ СОБЫТИЕ

В теории вероятностей для каждого эксперимента строится множество Ω элементарных исходов Ω = { , , ,...}, определяемое условием: результатом эксперимента всегда является ровно один исход из Ω.Сами элементы , , ,... называются элементарными исходами. Случайное событие - это некоторое множество, состоящее из элементарных исходов A = { , , ,...}. При этом исходы , , ,... называются благоприятствующими событию A. Поскольку не все элементарные исходы благоприятствуют событию A, случайное событие A при данном эксперименте может либо появиться, либо не появиться. Событие, которое происходит при любом эксперименте, называется достоверным и обозначается через E. Ясно, что достоверное событие содержит все элементарные исходы из Ω, то есть, E = Ω. Событие, не происходящее ни при одном эксперименте, называется невозможны м и обозначается через ∅; это событие не содержит ни одного элементарного исхода.

Произведением AB событий A и B называется новое событие, состоящее в одновременном появлении событий A и B. Суммой A + B называется событие, состоящее в появлении либо A, либо B, либо в их одновременном появлении. Разностью А\В называется событие, состоящее в появлении A и непоявлении B. Событие называется противоположным к событию A, если происходит при непоявлении А. Ясно, что A = ∅, A + = E. События A и B называются несовместными, если они не могут происходить одновременно. Ясно, что для несовместных событий AB = ∅.

Пример 1. Одновременно подбрасываются два кубика (игральные кости). Контролируется число очков на их верхних гранях. Описать множество элементарных исходов Ω и построить события: A = {в сумме выпадет 6 очков}, B = {суммарное число выпавших очков кратно 3}, C ={на кубиках выпало одинаковое число очков}.

Решение. Рассмотрим события: = {на верхней грани первого кубика выпадет k очков, второго - j очков, (k,j = 1,2,...,6). Ясно, что эти события являются элементарными исходами, поэтому Ω = { }. Событию A благоприятствуют исходы: , поэтому A = { }. Поскольку событие B п роисходит, если на верхних гранях в сумме выпадет 3 или 6, или 9, или 12 очков, то B ={ }. Очевидно C = { }.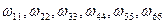

Пример 2. Из таблицы случайных чисел наудачу взято одно число. Вводятся события: A = {выбранное число делится на 5}, B = {выбранное число оканчивается нулем}. Выяснить смысл событий AB, A + B.

Решение. Согласно определению, АВ описывается так: выбранное число делится на 5 и одновременно оканчивается нулем, т.е. число, оканчивающееся нулем. Значит, AB = B. Согласно определению A + B описывается так: выбранное число или делится на 5, или оканчивается нулем, т.е. число, делящееся на 5. Значит, A + B = A.

Ответ: AB = B; A + B = A.

Пример 3. На рис 1.1 изображена электрическая схема. Вводятся события: A = {работает блок а}, ={работает блок , k=1,2}, C = {схема работает}. Записать выражение для C и .

Решение. Параллельное соединение блоков работает, если работает, хотя бы один из них, поэтому = {работает параллельное соединение блоков}. Событие С произойдет, если одновременно с этим работает блок a. Значит, C = A(). Схема не работает, если не работает или блок a, или параллельное соединение блоков , или и то, и другое сразу. Значит, .

Ответ: C = A (), .

 

 

Рис. 1.1.

 

В задачах 1.1-1.4 построить множество элементарных исходов и выразить через эти исходы указанные события.

1.1. Кубик (игральная кость) подбрасывается один раз. События: A = {на верхней грани выпало четное число очков}, B = {на верхней грани выпало число очков, кратное 3}.

1.2. Одновременно подбрасываются две монеты. События: A = {герб выпадает на одной монете}, B = {герб выпадает на двух монетах}.

1.3. Из четырех отобранных тузов наугад вытаскивается две карты. События: A = {обе карты черной масти}, B = {карты разного цвета}.

1.4. Монета подбрасывается три раза. События: A = {герб выпал ровно один раз}, B = {ни разу не выпала цифра}, C = {выпало больше гербов, чем цифр}, D = {герб выпал не менее чем два раза подряд}.

1.5. Три изделия проверяются на стандартность. Вводятся события: A = {все изделия стандартны}, B = {хотя бы одно изделие нестандартно}. Выяснить смысл событий A + B, AB, , A \ B.

1.6. Два шахматиста играют одну партию. Вводятся события: A ={выигрывает первый игрок}, B = {выигрывает второй игрок}.Описать события AB, \ B, , A + B + ().

1.7. Из колоды в 36 карт наугад вытаскивается карта. Вводятся события: A = {вытащен туз}, B = {вытащена карта красной масти}, C = {вытащена карта масти "пик"}. Выяснить смысл событий: AB, AC, BC,A \ B, B \ C, B \ A, , B + C.

1.8. Одновременно подбрасывается 4 монеты. Вводятся события: A = {гербов выпало больше, чем цифр}, B = {выпали все гербы}, C = {выпали все цифры}. Выяснить смысл событий: , , A \ B, A + B,AB, \С, ⋅ C, \ A.

1.9. Из урны, в которой находятся белые и черные шары, производится последовательное извлечение шаров. Вводятся события = {при k-ом извлечении появится белый шар}, k=1,2,3,... Описать события .

1.10. Двухмоторный самолет терпит аварию, если одновременно отказывают оба двигателя или выходит из строя системы управления. Вводятся события: = {выходит из строя k-ый двигатель}, k=1,2, B = {выходит из строя система управления}, C = {самолет терпит аварию}. Найти события C и .

1.11. Из двух коробок, в каждой из которых красные и синие карандаши, наугад берется по карандашу. Вводятся события: = {из k-ой коробки вытащен красный карандаш}, k=1,2. Построить множество элементарных исходов, выразив каждый элементарный исход через . Представить в алгебре событий следующие события: A = {вытащено два красных карандаша}, B = {вытащено два синих карандаша}, C ={вытащены карандаши одного цвета}, D = {вытащены карандаши разных цветов}.

1.12. Орудие дважды стреляет по цели. Пусть = {попадание в цель при k-ом выстреле}, k=1,2. Построить множество элементарных исходов, выразив каждый элементарный исход через . Представить в алгебре событий следующие события: A = {произойдет ровно одно попадание}, B = {не будет ни одного попадания}, C = {произойдет хотя бы одно попадание}, D = {произойдет хотя бы один промах}.

 

ВЫЧИСЛЕНИЕ КЛАССИЧЕСКОЙ ВЕРОЯТНОСТИ

Если некоторый эксперимент (опыт) имеет n равновозможных исходов, из которых k благоприятствуют появлению события А, то вероятность этого события находится по формуле

P (A) = k / n. (2.1)

При этом исходы эксперимента считаются равновозможными, если они имеют одинаковую возможность появиться. Напоминаем, что исход считается благоприятствующим, если событие A происходит при его появлении.

Пример 1. Датчик случайных чисел генерирует двузначное случайное число. Какова вероятность того, что сгенерированное число делится на 5?

Решение. Так как всего 90 двузначных чисел (от 10 до 99), то общее число исходов n=90. Число исходов, благоприятствующих нашему событию, равно k =17. Поэтому по формуле (2.1) получаем p = 17/90= 0,189.

Ответ: 0,189.

 

Во многих задачах вычисление классической вероятности ведется на основе формул комбинаторики. Большинство задач комбинаторики ставятся следующим образом. Имеется конечное множество X из элементов произвольной природы . Из этого множества выбирается k элементов и из них строится группа (). Если учитывается порядок расположения элементов внутри группы (т.е. группы, составленные из одних и тех же элементов, но расположенных в разном порядке, считаются разными), то такая группа называется размещением. Если порядок расположения элементов внутри группы не учитывается, то такая группа называется сочетанием. Размещение, cоставленное сразу из всех элементов множества X, называется перестановкой. Число размещений 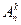, перестановок , сочетаний 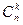находятся по формулам

(2.2)

 

(2.3)

 

(2.4)

 

При вычислении вероятностей часто используются также два основных правила комбинаторики: правило суммы и правило произведения.

Правило суммы. Если все группы элементов можно разбить на несколько классов, причем каждая группа входит только в один класс, то общее число групп равно сумме групп по всем классам.

Правило произведения. Если одну часть группы элементов можно выбрать способами, вторую часть группы - способами, то всю группу можно выбрать способами. При разбиении группы на s частей аналогично всю группу можно выбрать 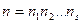способами.

Пример 2. Одновременно бросаются два кубика (игральные кости). Найти вероятность того, что суммарное число выпавших очков меньше 5.

Решение. Найдем n - общее число исходов. Так как с каждой из 6 граней одного кубика возможно появление любой из 6 граней другого кубика, то согласно правилу произведения . Число благоприятствующих исходов найдем простым их пересчетом: 1+1, 1+2, 1+3, 2+1, 2+2, 3+1, т.е. k=6. Следовательно, по формуле (2.1) p = k / n = 6/36= 1/6.

Ответ: 1/6.

Пример 3. В урне находятся 13 белых и 17 черных шаров. Извлекаются 5 шаров. Найти вероятности событий: А = {извлечено два белых шара}, В = {извлечен хотя бы один белый шар}.

Решение. Найдем общее число исходов. Вытащить 5 шаров – означает составить группу из 5 шаров, если всего их 30, причем порядок извлечения шаров безразличен. Значит, речь идет о сочетаниях по 5 элементам из 30. Число таких сочетаний равно , и по формуле (2.4)

 

 

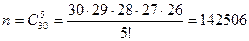
Найдем число исходов, благоприятствующих событию A. Исход благоприятствует A, если из 13 белых шаров извлечем два, а из 17 черных шаров - три, причем порядок извлечения безразличен. Поэтому согласно правилу произведения число исходов, благоприятствующих А, равно

 

 

Теперь по формуле (2.1) .

Чтобы решить вторую часть задачи, введем в рассмотрение противоположное событие 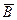= {извлечены все черные шары}. Число исходов, благоприятствующих 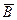, равно = = 6188. Значит,

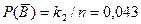и .

Ответ: 0,372; 0,957.

Пример 4. Слово АБРАКАДАБРА разрезается на буквы, которые затем буквы перемешиваются. Одна за другой вытаскиваются 5 букв и прикладываются друг к другу слева направо. Найти вероятности событий: A = {случайно сложится слово РАДАР}, B = {случайно сложится слово БАРКА}.

Решение. Находим n - общее число исходов. Всего 11 букв, из них набирается группа в 5 букв, порядок внутри должен учитываться (ибо слово - упорядоченная группа букв). Значит, речь идет о размещении. По формуле (2.2)

.

 

Найдем число исходов, благоприятствующих слову РАДАР. В исходном слове АБРАКАДАБРА содержится 2 буквы "Р", 5 букв "А", 1 буква "Д". Поэтому в слове РАДАР первую букву "Р" можно выбрать двумя способами, а вторую - всего лишь одним (одна "Р" уже взята). Первую букву "А" можно выбрать 5 способами, вторую - 4 способами. Букву "Д"- одним способом. По правилу произведения число благоприятствующих исходов равно 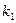= 2 ⋅ 5 ⋅ 1 ⋅ 4 ⋅ 1 = 40. Следовательно,

P(A) = 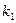/n = 40 / 55440 = 7,22 ⋅

Аналогично число исходов, благоприятствующих слову БАРКА, равно = 2 ⋅ 5 ⋅ 2 ⋅ 1 ⋅ 4 = 80. Следовательно, P(B) = /n = 80 / 55440 = 1,44 ⋅ .

Ответ: 7,22 ⋅ ; 1,44 ⋅ ..

Пример 5. Десять книг, из которых три по математике, случайным образом расставляются на полке. Найти вероятность того, что книги по математике окажутся рядом.

Решение. Общее число исходов равно числу перестановок из 10 книг, т.е. согласно (2.3) n = = 10!. Чтобы найти число благоприятствующих исходов, рассмотрим одну фиксированную расстановку книг на полке (см. рис. 2.1).

 

Рис. 2.1.

 

Здесь первые три позиции занимают книги по математике, на 4-10 позициях поставлены остальные семь книг. Сколькими способами можно получить такую расстановку? На первых трех позициях книги по математике можно ра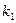сставить = = 3! способами, на остальных позициях другие книги можно расставить = = 7! способами. Поэтому согласно правилу произведения вся расстановка книг, изображенная на рис 2.1, может быть получена = 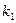⋅ = 3!⋅7! способами. Чтобы получить все требуемые условием задачи расстановки книг, нужно тройку книг по математике переставить с 1-3 позиций на 2-4, 3-5,..,8-10 позиции, не изменяя порядок расположения книг внутри "математической" и "нематематической" групп. Таких "сдвижек" будет 8, и для каждой такой "сдвижки"

возможна перестановка книг внутри "математической" и "нематематической" групп способами. Значит, общее число благоприятствующих исходов равно k = 8 = 8 ⋅ 3!⋅7!. Вероятность события находим по формуле (2.1) и получаем

p = k/n = 8 ⋅ 3! ⋅ 7!/10! = 1/ 15 = 0,067.

Ответ: 0,067.

Пример 6. Пять мужчин и десять женщин случайным образом по трое рассаживаются за 5 столиков. Какова вероятность того, что за каждым столиком окажется мужчина?

Решение. Найдем сначала общее число исходов. За первый столик могут сесть любые три человека из 15, такая посадка осуществляется способами. За второй столик может сесть любая тройка из оставшихся 12 человек, такая посадка осуществляется способами.

Аналогично посадку за 3,4,5 столики можно осуществить , , способами. Поэтому по правилу произведения общее число исходов равно

n = ⋅ ⋅ ⋅ ⋅ = ⋅ ⋅ ⋅ ⋅ = 15! / .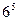

Аналогично одного мужчину и две женщины за первый столик можно посадить

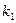= 5⋅ способами, за второй, третий, четвертый, пятый столики - соответственно способами. Значит, число благоприятствующих исходов равно

k = 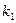⋅ ⋅ ⋅ ⋅ = 5!⋅ ⋅ ⋅ ⋅ = 5!⋅10!/ .

Следовательно,

 

Ответ: 0,081.

 

2.1. В магазин поступило 30 новых телевизоров, среди которых 5 имеют скрытые дефекты. Найти вероятность того, что купленный телевизор не имеет скрытых дефектов.

2.2. Игральная кость подбрасывается один раз. Найти вероятности событий: A = {число очков на верхней грани равно 6}, B = {число очков кратно 3}, C = {число очков меньше 5}.

2.3. Из колоды в 36 карт наугад вытаскивается одна. Найти вероятности событий: A = {карта имеет масть "пик"}, B = {карта имеет черную масть}, C = {вытащен туз}, D = {вытащен туз "пик"}.

2.4. Куб, все грани которого окрашены, распилен на 1000 кубиков одинакового размера. Кубики перемешиваются, а затем наугад вытаскивается один из них. Найти вероятности событий: A = {кубик имеет три окрашенные грани}, B = {кубик имеет две окрашенные грани}, C = {кубик имеет одну окрашенную грань}.

2.5. На шахматную доску случайным образом ставят две ладьи: белую и черную. Какова вероятность того, что ладьи не бьют друг друга?

2.6. На 9 карточках написаны цифры от 1 до 9. Определить вероятность того, что число, составленное из двух наугад взятых карточек, делится на 18.

2.7. На 8 карточках написаны числа: 2,4,6,7,8,11,12,13. Из двух наугад взятых карточек составлена дробь. Какова вероятность того, что она сократима?

2.8. Одновременно подбрасывается две кости. Найти вероятности событий: A = {количество очков на верхних гранях одинаково}, B = {на верхних гранях выпадет в сумме 8 очков}, C = {сумма очков четна}, D ={хотя бы на одной кости появится цифра 6}.

2.9. Телефонный номер состоит из 6 цифр. Некто забыл номер телефона, но помнит, что он состоит из нечетных цифр. Какова вероятность того, что номер будет угадан с первой попытки?

2.10. Поезд метро состоит из 6 вагонов. Какова вероятность того, что

3 пассажира сядут в один вагон?

2.11. Зенитная батарея, состоящая из n орудий, производит залп по группе из m самолетов. Каждое орудие выбирает себе цель наудачу независимо от остальных. Найти вероятность того, что все орудия выстрелят по одному самолету.

2.12. Пяти радиостанциям разрешено вести передачи на шести частотах. Каждая радиостанция наудачу выбирает себе частоту. Найти вероятности событий: A = {все радиостанции работают на одной частоте}, B = {хотя бы две радиостанции работают на разных частотах}, C = {все радиостанции работают на разных частотах}.

2.13. Числа 1,2,...,20 написаны на карточках. Карточки тщательно перетасовываются, а затем вытаскиваются две из них. Какова вероятность того, что сумма чисел на вынутых карточках равна 30?

2.14. Цветочница выставила на продажу 15 белых и 10 красных роз. Некто просит подобрать ему букет из 5 роз. Какова вероятность того, что в букете будет 2 белые и 3 красные розы?

2.15. В экзаменационный билет включается два теоретических вопроса. Студент из 60 вопросов программы выучил только 40. Найти вероятности событий: A = {студент знает оба вопроса билета}, B = {студент знает только один вопрос билета}, C = {студент знает хотя бы один вопрос билета}.

2.16. На 10 карточках написаны буквы: А, А, А, А, А, А, М, М, М, М. Ребенок наугад вытаскивает одну за другой 4 карточки и прикладывает их друг к другу слева направо. Какова вероятность того, что он случайно сложит слово МАМА?

2.17. Слово МАТЕМАТИКА разрезается на буквы. Буквы перемешиваются и снова складываются слева направо. Найти вероятность того, что снова получится слово МАТЕМАТИКА.