Существует круг задач, решение которых основано на геометрической интерпретации вероятности. Итак, на прямой выберем отрезок Е и внутри него отрезок (или совокупность отрезков) A (см. рис.3.1). Внутрь отрезка E "бросается" точка. Вероятность ее попадания на A находится по формуле
 , (3.1)
, (3.1)
где 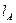 и
и  - длины A и E соответственно.
- длины A и E соответственно.
Вероятность события A, найденная по формуле (3.1), называется геометрической вероятностью на прямой.
Аналогично, если точка "бросается" внутрь квадрата E (см. рис.3.2), то вероятность ее попадания в область A, лежащую внутри E, находится
по формуле
 , (3.2)
, (3.2)
где  и
и  - площади A и E соответственно.
- площади A и E соответственно.
Вероятность попадания точки внутрь трехмерной области A при ее "бросании" внутрь куба E аналогичным образом находится по формуле  , где
, где  и
и  - объемы A и E соответственно.
- объемы A и E соответственно.


Рис. 3.1. Рис. 3.2.
Пример 1. На прямолинейном участке газопровода длиной 80 км произошел разрыв. Какова вероятность того, что разрыв удален от обоих концов участка на расстояние, большее 30 км?

Рис. 3.3.
Решение. Участок газопровода AB разобьем точками C, D на три части, как показано на рис. 3.3. В нашем случае разрыв газопровода должен произойти на участке CD. Значит, вероятность события равна
 = 20/80 = 0,25.
= 20/80 = 0,25.
Ответ: 0.25.
Пример 2. Быстро вращающийся диск разделен на 6 одинаковых секторов, попеременно окрашенных в красный и белый цвета. По диску произведен выстрел, и пуля попала в диск. Найти вероятность того, что пуля попала в один из красных секторов.
Решение. Пусть R - радиус диска, тогда  - его площадь,
- его площадь, 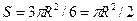 - суммарная площадь красных секторов. Значит, вероятность попадания в красный сектор равна
- суммарная площадь красных секторов. Значит, вероятность попадания в красный сектор равна  = 0,5.
= 0,5.
Ответ: 0,5.
Пример 3. Наугад берутся два числа из отрезка [0;2]. Найти вероятность того, что их сумма больше 2, а сумма их квадратов меньше 4.
Решение. Пусть x,y- выбранные числа. Выбрать произвольно два
 числа x, y
числа x, y  [0;2] означает в нашей задаче бросить наугад точку M(x,y) внутрь квадрата 0 ≤ x,y ≤ 2 (см. рис. 3.4). Указанное в условии задачи событие произойдет, если будут выполнены условия: x+y>2,
[0;2] означает в нашей задаче бросить наугад точку M(x,y) внутрь квадрата 0 ≤ x,y ≤ 2 (см. рис. 3.4). Указанное в условии задачи событие произойдет, если будут выполнены условия: x+y>2,
Рис. 3.4.  , т.е. если брошенная точка
, т.е. если брошенная точка
попадет внутрь области A, ограниченной линиями: x + y = 2;  (см. рис. 3.4). Поэтому вероятность события
(см. рис. 3.4). Поэтому вероятность события
можно найти по формуле  , где
, где  - площадь квадрата,
- площадь квадрата,  -площадь области А. Находим
-площадь области А. Находим 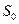 = 2 ⋅ 2 = 4,
= 2 ⋅ 2 = 4,

Следовательно, p = (π − 2) / 4.
Ответ: (π -2)/4.
Пример 4. Два приятеля договорились о встрече в промежутке времени между 9ч. и 9ч.30мин. Первый пришедший ждет второго 15 минут и уходит. Какова вероятность того, что встреча состоится?
Решение. Выберем 9 часов за начало отсчета. Пусть x и y – моменты прихода первого и второго приятеля соответственно. Согласно условию задачи 0 ≤ x,y ≤ 0,5. Встреча состоится, если | x − y |≤ 0,25. Значит, достоверное событие моделируется на плоскости xOy квадратом [0;0,5] × [0;0,5] (см. рис. 3.5), а событие A ={встреча состоится} – областью внутри квадрата, задаваемой неравенством  | x − y |≤ 0,25, (на рис 3.5 эта область заштрихована). Площадь квадрата
| x − y |≤ 0,25, (на рис 3.5 эта область заштрихована). Площадь квадрата  = 0,25, площадь фигуры равна
= 0,25, площадь фигуры равна
 =
=  −2⋅0,5⋅
−2⋅0,5⋅  = 0,1875.
= 0,1875.
Значит, P(A) =  /
/  = 0,75.
= 0,75.
Рис. 3.5.
Ответ: 0,75.
3.1. В точке C, положение которой на телефонной линии AB длины  равновозможно, произошел разрыв. Определить вероятность того, что C удалена от A на расстояние, большее l.
равновозможно, произошел разрыв. Определить вероятность того, что C удалена от A на расстояние, большее l.
3.2. На отрезок длины l поставлена точка деления. Определить вероятность того, что меньший отрезок имеет длину больше, чем l/3.
3.3. В окружность вписывается прямоугольник. Какова вероятность, что его высота больше длины основания? При решении задачи использовать понятие геометрической вероятности.
3.4. В окружности радиуса R проводятся вертикальные хорды. Какова вероятность того, что длина наудачу взятой хорды окажется меньше радиуса?
3.5. Кусок проволоки длиной 20 см был согнут в наудачу выбранной точке. После этого, перегнув проволоку еще в двух местах (не ломая ее), сделали прямоугольную рамку. Найти вероятность того, что площадь полученной рамки не превосходит 21см 2.
3.6. В окружность радиуса R вписан правильный треугольник. Внутрь круга бросается точка. Найти вероятность того, что точка попадет внутрь треугольника.
3.7. Два приятеля договорились встретиться в течение часа. Первый из пришедших ждет 10 минут, а потом уходит. Какова вероятность того, что встреча состоится?
3.8. В любой момент времени из промежутка длительностью Т равновозможны поступления в приемник двух сигналов. Определить вероятность того, что промежуток времени между сигналами будет меньше t.