ФОРМУЛЫ ПУАССОНА И МУАВРА-ЛАПЛАСА

Если в схеме независимых испытаний число n велико, пользоваться формулой Бернулли (6.1) не рекомендуется, так как в этом случае требуются значительные по объему вычисления. Если число испытаний велико, а p мало и при этом произведение , то вероятность 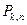можно приближенно найти по формуле Пуассона

, k=0,1,2,…. (7.1)

Вычисления по формуле (7.1) упрощаются, если использовать Таблицу III приложения [1].

Если число испытаний велико, а произведение , то вероятность находится по локальной формуле Муавра-Лапласа

, k = 0,1,2,..., (7.2)

где - функция Гаусса (Таблица I приложения [1]).

Следует помнить, что 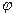(x) - четная функция, т.е. 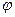(− x) = 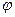(x), и 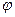(x) = 0 при x > 4. Поэтому в большинстве таблиц значения функции приведены только для значений аргумента x [0;4].

Вероятность того, что частота k наступлений события А попадет в промежуток при тех же условиях находится по интегральной формуле Муавра- Лапласа

(7.3)

где

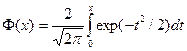
Функция Φ(x) называется функцией Лапласа, она тоже затабулирована (Таблица II приложения [1]). Следует помнить, что функция Ф(х) нечетна, т.е. Φ (− x) = −Φ (x), и Φ (x) ≈ 1 при x > 5. Поэтому в большинстве таких таблиц значения функции Φ (x) приведены только для значений аргумента x [0;5]. Следствием формулы (7.3) являются следующие формулы:

(7.4)

(k – частота появлений события А в n испытаниях) и

. (7.5)

Пример 1. Вероятность набора абонентом телефонного номера с ошибкой равна 0,001. Определить вероятность того, что среди 500 произведенных заказов не более 2 телефонных номеров были набраны с ошибкой.

Решение. Искомая вероятность равна . Согласно условию n = 500, p = 0,001. Так как p мало, для вычисления вероятностей используем формулу Пуассона (7.1). Находим λ = np = 500⋅0,001 = 0,5 . Следовательно, искомая вероятность равна (Таблица III, [1])

= 0,65+0,3033 + 0,0758=0,9856.

Ответ: 0,9856.

Пример 2. Вероятность изделию быть бракованным равна 0,05. Найти вероятность того, что среди 1000 изделий а) 40 бракованных; б) число бракованных находится в промежутке от 40 до 70 включительно.

Решение. Испытание изделий на брак удовлетворяет схеме испытаний Бернулли. Вероятность для каждого изделия быть бракованным p = 0,05, а не бракованным q = 0,95. Испытаниям подвергаются n = 1000 изделий.

а) k =40; находим по формуле Муавра – Лапласа (7.2). Определяем необходимые величины: np = 50, npq = 47,5, ; 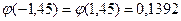(Таблицa I приложения [1]).

Окончательно получаем .

б) находим по интегральной формуле Муавра – Лапласа (7.3) при и .

Ответ: а) 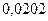; б) .

Пример 3. Вероятность приема сообщения без ошибок равна 0,5. Найти вероятность того, что из 100 независимо друг от друга принятых сообщений число принятых без ошибок будет отличаться от 50 по абсолютной величине не более чем на 5.

Решение. В условиях задачи А – сообщение принято без ошибок . Необходимо найти Применяем формулу (7.4) при .

.

При нахождении Ф(1) использовалась Таблицы II приложения [1].

Ответ: 0,6827.

Пример 4. Вероятность того, что деталь не стандартная, равна 0,2. Определить вероятность того, что среди случайно отобранных 2500 деталей частость появления нестандартных деталей отклонится от вероятности по абсолютной величине не более, чем на 0,004.

Решение. Применим формулу (7.5) при n = 2500; p = 0,2; q = 0,8, npq = 400.

.

Значение функции Ф(0,5) найдено с использованием Таблицы II приложения [1].

Ответ: .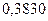

 

7.1. Вероятность выпуска сверла повышенной хрупкости (брак) равна 0,002. Сверла укладываются в коробки по 100 штук. Найти вероятность того, что: а) в коробке не окажется бракованных сверл; б) число бракованных сверл окажется не более 3.

7.2. Магазин получил 1000 стеклянных бутылок минеральной воды. Вероятность того, что при перевозке бутылка будет разбита, равна 0,003. Найти вероятность того, что при перевозке будут разбиты: а) ровно две бутылки; б) не более двух бутылок; в) не менее двух бутылок; г) хотя бы одна бутылка.

7.3. Если левши составляют в среднем 1% населения, каковы шансы на то, что среди 200 человек: а) окажутся ровно четверо левшей; б) окажутся не менее четырех левшей.

7.4. Известно, что в среднем 5% студентов носят очки. Какова вероятность того, что из 200 студентов, сидящих в аудитории, не менее 5 носят очки?

7.5. Система связи состоит из 1000 элементов, каждый из которых независимо от остальных выходит из строя за время Т с вероятностью 0,0005. Найти вероятности следующих событий: А= {за время Т откажет хотя бы один элемент}, В= {за время Т откажут ровно 3 элемента}, С={за время Т откажут не более 3 элементов}.

7.6. Корректура в 500 страниц содержит 1300 опечаток. Найти наиболее вероятное число опечаток на одной странице текста и вероятность этого числа опечаток.

7.7. На факультете 500 студентов. Найти наиболее вероятное число студентов, родившихся 1 сентября, и вероятность этого числа рождений. Вероятность рождения 1 сентября принять равной 0,0027.

7.8. Вероятность изготовления консервной банки с недостаточной герметизацией равна 0,002. Среди скольких банок, отобранных случайно, можно с вероятностью 0,9 ожидать отсутствие бракованных?

7.9. На АТС поступают в среднем 12 заказов в минуту. Найти вероятность того, что за 20 с поступят: а) ровно 2 заказа; б) не менее 2 заказов.

7.10. Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.

7.11. Вероятность изготовления обуви первого сорта равна 0,4. Какова вероятность того, что среди 600 пар обуви, поступивших на контроль, количество пар первосортной обуви колеблется в пределах от 228 до 252?

7.12. Орудия обстреливают ДОТ. Вероятность попадания при каждом выстреле равна 0,2. ДОТ окажется пораженным, если в него попадут не менее 30 снарядов. Какова вероятность поражения ДОТа, если по нему выпущены 100 снарядов?

7.13. Вероятность пошива костюма 1 сорта равна 0,8. В магазин поступили 400 костюмов. Найти вероятности следующих событий: А={число первосортных костюмов равно 310}, В={число первосортных костюмов не превысит 310}.

7.14. Вероятность изготовления на заводе первосортного холодильника составляет 0,9. В магазин поступили 100 холодильников. Какова вероятность, что среди них: а) ровно 92 первосортных; б) число первосортных холодильников колеблется в пределах от 80 до 90.

7.15. Лабораторным путем установлена всхожесть зерен в 80%. Чему равна вероятность того, что среди отобранных 1000 зерен прорастут: а) не менее 800 зерен; б) от 820 до 840 зерен; в) от 880 до 920 зерен? Определить вероятность того, что среди отобранных 1000 зерен число проросших отличается от наиболее вероятного числа их не более чем на 30 зерен в ту или другую сторону.

 

 

ОТВЕТЫ

 

 

8.1. Ответы к разделу 1

 

1.1. , где - выпало k очков, k =1,2,...,6; А = { ω2,ω4,ω6 }, B = { , }. 1.2. Ω = {ГГ, ГЦ, ЦГ, ЦЦ}, А = {ГЦ, ЦГ}, B = {ГГ}, где Г - герб, Ц - цифра. 1.3. Ω= {БК, БП, БЧ, КП, КЧ, ПЧ}, А = {КП}, B = {БК, БП, КЧ}, где Б, К, П, Ч - тузы "бубен", "крести", "пики", "червы" соответственно. 1.4. Ω = {ГГГ, ЦГГ, ГЦГ, ГГЦ, ГЦЦ, ЦГЦ, ЦЦГ, ЦЦЦ};

А = {ГЦГ, ЦГЦ, ЦЦГ}; B = {ГГГ}; C = {ГГГ, ЦГГ, ГЦГ, ГГЦ}; D = {ГГГ, ЦГГ, ГГЦ}.

1.5. A+B=E; AB = ∅; ; A\B=A; 1.6. ∅, ничья, В, Е. 1.7. АВ = {вытащен туз "бубен" или туз "черви"}, АС = {вытащен туз "пик"}, ВС = ∅, А\В = {вытащен туз черной масти}, В\С=В, В\А = {вытащена карта красной масти, не являющаяся тузом}, В С =В, В+С = {вытащенная карта не имеет масть "треф"}. 1.8. = {гербов выпало не больше, чем цифр}, = {среди выпадений есть и цифры}, А\В = {выпадает ровно три герба}, А+В = А, АВ = В, А\С = {выпадает 1 или 2 герба}, АС = С, \А = {выпадает 1 или 2 герба}.

1.9. При двух извлечениях сначала появится черный, затем белый шар; при четырех извлечениях черный шар появится только последним; при четырех извлечениях цвет шаров меняется попеременно. 1.10. и .

1.11. , , , . 1.12. .

 

8.2. Ответы к разделу 2

 

2.1. 5/6. 2.2. 1/6; 1/3; 2/3. 2.3. 1/4; 1/2; 1/9; 1/36. 2.4. 0,008; 0,096; 0,384. 2.5. 7/9. 2.6. 1/18. 2.7. 5/14. 2.8. 1/6; 5/36; 1/2; 11/36. 2.9. ; 2.10. 1/36. 2.11. . 2.12. ; 1 − ; 5!/ . 2.13. 1/38. 2.14. 0,237. 2.15. 0,441; 0,452; 0,893. 2.16. 1/14. 2.17. 24/10!.

 

8.3. Ответы к разделу 3

 

3.1. . 3.2. 1/3. 3.3. 0,5. 3.4. . 3.5. 0,6. 3.6. 0,413. 3.7. 11/36. 3.8. .

 

8.4. Ответы к разделу 4

 

4.1. 0,06554. 4.2. 0,06. 4.3. 1/216; 1/36. 4.4. 0,56; 0,38; 0,94. 4.5. 0,612; 0,329; 0,388. 4.6. 0,343; 0,441; 0,216. 4.7. 0,096; 0,384; 0,992. 4.8. . 4.9. 0,00122. 4.10. 0,320. 4.11. 0,745. 4.12. 0,0714. 4.13. . 4.14. ; ; .

 

 

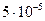8.5. Ответы к разделу 5

5.1. 0,9987. 5.2. 0,987. 5.3. 0,895. 5.4. 0,067. 5.5. 0,158. 5.6. 0,1704. 5.7. 0,5. 5.8. Одинаковы. 5.9. 0,22. 5.10. 0,56. 5.11. 0,445. 5.12. 0,3. 5.13. 0,429; 0,571. 5.14. 0,903. 5.15. 9/47.

 

8.6. Ответы к разделу 6

6.1. 5/32; 5/16; 5/16. 6.2. 80/243. 6.3. 0,060; 0,185. 6.4. 0,00038; 0,8999. 6.5. 0,0064; 0,0512; 0,99968; 0,942. 6.6. 0,31; 0,48; 0,52; 0,62. 6.7. 0,375. 6.8. Выиграть одну партию из двух; выиграть не менее двух партий из четырех. 6.9. 8. 6.10. 5.

 

8.7. Ответы к разделу 7

7.1. 0,819; 0,999. 7.2. 0,224; 0,423; 0,801; 0,950. 7.3. 0,09; 0,143 7.4. 0,971.

7.5. 0,394; 0,013; 0,998. 7.6. 2; 0.251. 7.7. 1; 0,3481. 7.8. 53. 7.9. 0,146;

0,908.. 7.10. 0,0456. 7.11. 0,683. 7.12. 0,0062. 7.13. 0,023; 0,106. 7.14.0,106;

0,4995. 7.15. 0,5; 0,0564; 0; 0,9822.

 

СПИСОК ЛИТЕРАТУРЫ

 

1. Кремер Н. Ш. Теория вероятностей и математическая статистика. М.: Юнити, 2002. -543с.
2. Сборник задач по математике для втузов. Теория вероятностей и математическая статистика: Учеб. пособие для втузов /Под ред. А. В. Ефимова.- М.: Наука, 1990.- 428 с.
3. Гмурман В. Е. Руководство к решению задач по теории вероятности и математической статистике: Учеб. пособие для студентов втузов М.: Высшая школа, 1979.- 400 с.
4. Лозинский Н. С. Сборник задач по теории вероятностей и математической статистике: Учеб. пособие для студентов экономических специальностей вузов. - М.: Статистика, 1975.- 200 с.
5. Вентцель Е. С., Овчаров Л. А. Теория вероятностей. М.: Наука, 1973.- 386 с.
6. Сборник задач по теории вероятностей, математической статистики м теории случайных функций. / Под ред. А. А. Свешникова.- М.: Наука, 1970.- 656 с.
7. Емельянов Г. В., Скитович В. П. Задачник по теории вероятностей и математической статистике Л.: Изд-во Ленинград. ун-та, 1967.- 332 с.