Допустим, производится эксперимент (опыт), об условиях которого можно сделать n взаимно исключающих друг друга предположений (гипотез):  . Каждая гипотеза представляет из себя некоторое событие; все они попарно несовместны и образуют полную группу (т.е. в результате эксперимента может реализоваться ровно одна из гипотез). Вероятности гипотез должны быть предварительно найдены; пусть они равны P(
. Каждая гипотеза представляет из себя некоторое событие; все они попарно несовместны и образуют полную группу (т.е. в результате эксперимента может реализоваться ровно одна из гипотез). Вероятности гипотез должны быть предварительно найдены; пусть они равны P( ), P (
), P ( ),..., P(
),..., P( ). Отметим, что если при решении задачи гипотезы введены правильно, и их вероятности найдены верно, то справедливо равенство
). Отметим, что если при решении задачи гипотезы введены правильно, и их вероятности найдены верно, то справедливо равенство
P( ) + P(
) + P( ) +... + P (
) +... + P ( ) = 1.
) = 1.
Если равенство не выполняется, это говорит о том, что либо система гипотез введена неверно, либо имеются ошибки в вычислении вероятностей
гипотез.
Далее рассматривается некоторое событие A, вероятность которого нужно определить. При этом сначала находятся условные вероятности P(A /  ), P(A /
), P(A /  ),..., P(A /
),..., P(A /  ). Затем вероятность события А находится по следующей формуле полной вероятности
). Затем вероятность события А находится по следующей формуле полной вероятности
 (5.1)
(5.1)
Вероятности P( ), i=1, 2,..., n, вычисляются до проведения эксперимента. В зависимости от появления или непоявления события A в результате эксперимента вероятности гипотез могут быть уточнены. Условные вероятности гипотез
), i=1, 2,..., n, вычисляются до проведения эксперимента. В зависимости от появления или непоявления события A в результате эксперимента вероятности гипотез могут быть уточнены. Условные вероятности гипотез 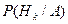 могут быть найдены с помощьюформулы Байеса (или Бейеса)
могут быть найдены с помощьюформулы Байеса (или Бейеса)
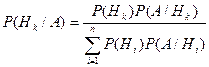 , k=1,2,…,n. (5.2)
, k=1,2,…,n. (5.2)
Пример 1. В сборочный цех поступают детали с трех поточных линий. Производительности этих линий относятся как 5:3:2. Вероятность брака для первой линии составляет 0,01; для второй линии - 0,02; для третьей линии - 0,03. Найти вероятность того, что наугад взятая деталь бракована.
Решение. Пусть А = {взятая деталь бракована}. Введем систему гипотез: 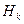 ={деталь изготовлена на k-й линии}, k=1, 2, 3. Находим вероятности гипотез
={деталь изготовлена на k-й линии}, k=1, 2, 3. Находим вероятности гипотез
 ;
; 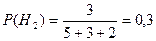 ;
; 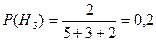
Согласно условию задачи условные вероятности события А равны
P(A /  ) = 0,01; P(A/
) = 0,01; P(A/  ) = 0,02; P(A/
) = 0,02; P(A/  ) = 0,03.
) = 0,03.
Применим формулу полной вероятности (5.2).
P(A) = P ( ) P (A /
) P (A /  ) + P(
) + P( ) P(A /
) P(A /  ) + P (
) + P ( ) P (A /
) P (A /  ) =
) =
= 0,5 ⋅ 0,01 + 0,3 ⋅ 0,02 + 0,2 ⋅ 0,03 = 0,017.
Ответ: 0,017.
Пример 2. На уничтожение цели противника вылетело два самолета разных типов. Самолет первого типа может уничтожить цель с вероятностью 0,9, второго типа - с вероятностью 0,8. Однако противовоздушная оборона противника может сбить самолет первого типа с вероятностью 0,95, самолет второго типа - с вероятностью 0,85. Какова вероятность уничтожения цели?
Решение. Пусть A = {цель уничтожена}. Введем систему гипотез:
 = {оба самолета не прорвались к цели};
= {оба самолета не прорвались к цели};
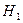 = {только самолет первого типа прорвался к цели};
= {только самолет первого типа прорвался к цели};
 = {только самолет второго типа прорвался к цели};
= {только самолет второго типа прорвался к цели};
 = {оба самолета прорвались к цели}.
= {оба самолета прорвались к цели}.
Находим вероятности гипотез
P( ) = 0,95 ⋅ 0,85 = 0,8075; P(
) = 0,95 ⋅ 0,85 = 0,8075; P(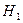 ) = 0,05 ⋅ 0,85 = 0,0425;
) = 0,05 ⋅ 0,85 = 0,0425;
P( ) = 0,95 ⋅ 0,15 = 0,1425; P(
) = 0,95 ⋅ 0,15 = 0,1425; P( ) = 0,05 ⋅ 0,15 = 0,0075.
) = 0,05 ⋅ 0,15 = 0,0075.
Находим условные вероятности события А.
P(A /  ) = 0; P(A/
) = 0; P(A/ 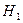 ) = 0,9; P(A/
) = 0,9; P(A/  ) = 0,8;
) = 0,8;
P(A /  ) = 0,9 + 0,8 + 0,9 ⋅ 0,8 = 0,98.
) = 0,9 + 0,8 + 0,9 ⋅ 0,8 = 0,98.
Теперь по формуле (5.2)
P(A) = 0,8075 ⋅ 0 + 0,0425 ⋅ 0,9 + 0,1425 ⋅ 0,8 + 0,0075 ⋅ 0,98 = 0,1596.
Ответ: 0,1596.
Пример 3. Партия микросхем, среди которых 10% неисправных, поступила на проверку. Используется упрощенный тест проверки, по которому с вероятностью 0,95 дефектная микросхема признается дефектной и с вероятностью 0,03 исправная микросхема признается дефектной. Наудачу протестированная микросхема признана дефектной. Какова вероятность того, что на самом деле микросхема является исправной?
Решение. Пусть A = {наудачу протестированная микросхема признана дефектной}. Введем систему гипотез: 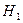 = {тестируется дефектная микросхема},
= {тестируется дефектная микросхема},  = {тестируется исправная микросхема}. Находим вероятности гипотез P(
= {тестируется исправная микросхема}. Находим вероятности гипотез P(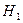 ) = 0,1; P(
) = 0,1; P(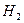 ) = 0,9. Условные вероятности события равны P(A /
) = 0,9. Условные вероятности события равны P(A / 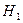 ) = 0,95; P (A /
) = 0,95; P (A / 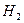 ) = 0,03. По формуле Байеса (5.2) находим
) = 0,03. По формуле Байеса (5.2) находим
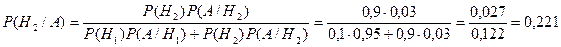
Ответ: 0,221.
Пример 4. В группе из 10 студентов, пришедших на экзамен, 3 студента подготовлены отлично, 4 - хорошо, 2 - удовлетворительно и 1 -плохо. В экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент может ответить на все 20 вопросов, хорошо подготовленный - на 16, удовлетворительно подготовленный - на 10, плохо подготовленный - на 5. Вызванный наугад студент ответил на все три заданных
преподавателем вопроса. Найти вероятность того, что этот студент: а) подготовлен отлично; б) подготовлен плохо.
Решение. Пусть событие А={студент ответил все три вопроса}. Введем систему гипотез:
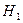 ={студент подготовлен отлично};
={студент подготовлен отлично};
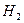 ={студент подготовлен хорошо};
={студент подготовлен хорошо};
 ={студент подготовлен удовлетворительно};
={студент подготовлен удовлетворительно};
 ={студент подготовлен плохо}.
={студент подготовлен плохо}.
Находим вероятности гипотез.
P(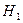 ) = 0,3; P (
) = 0,3; P (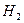 ) = 0,4; P (
) = 0,4; P ( ) = 0,2; P (
) = 0,2; P ( ) = 0,1.
) = 0,1.
Находим условные вероятности события А.
P(A / 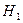 ) = 1; P(A /
) = 1; P(A / 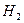 ) = 16 / 20 ⋅ 15 / 19 ⋅ 14 / 18 = 0,491;
) = 16 / 20 ⋅ 15 / 19 ⋅ 14 / 18 = 0,491;
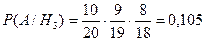 ;
; 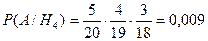
По формуле Байеса (5.2) находим
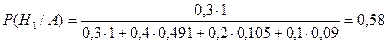
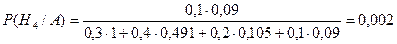
Ответ: 0,58; 0,002.
5.1. В цехе 14 установок с автоматическим контролем и 6 с ручным. Вероятность изготовления некондиционной продукции для установок с автоматическим контролем составляет 0,001, с ручным контролем - 0,002. Какова вероятность того, что взятая на лабораторный анализ продукция цеха оказалась кондиционной?
5.2. На конвейер поступают детали с двух станков с ЧПУ. Производительность первого станка в 2 раза больше производительности второго. Вероятность брака на первом станке 0,01, на втором станке 0,02. Найти вероятность того, что наудачу взятая деталь стандартна.
5.3. В продажу поступают телевизоры трех заводов. Продукция первого завода содержит 20% телевизоров со скрытым дефектом, второго 10%, третьего 5%. Какова вероятность приобрести исправный телевизор, если в магазин поступило 30 телевизоров первого завода, 20 второго, 50 третьего.
5.4. В бригаде 8 рабочих и 2 ученика. Вероятность изготовить бракованное изделие для рабочего составляет 0,05, для ученика 0,2. Производительность рабочего в два раза выше, чем у ученика. Какова вероятность, что некоторое изделие, изготовленное бригадой, окажется бракованным?
5.5. В студенческой группе 3 отличника, 5 хорошо успевающих, 12 слабо успевающих студента. Отличник с равной вероятностью может получить на экзамене 5 или 4; хорошо успевающий студент - с равной вероятностью 5 или 4, или 3; слабо успевающий - с равной вероятностью 3 или 2. Какова вероятность, что наугад вызванный сдавать экзамен студент получит оценку 4?
5.6. Вероятность попадания в танк при одном выстреле составляет 0,2. При одном попадании танк загорается с вероятностью 0,3, при двух с вероятностью 0,5, при трех - с вероятностью 0,9. По танку сделано три выстрела. Какова вероятность его загорания?
5.7. Имеется 15 экзаменационных билетов, каждый из которых содержит по 2 вопроса. Студент Иванов знает ответ только на 15 вопросов. Определить вероятность того, что он сдаст экзамен, если для этого нужно ответить либо на оба вопроса, либо на один вопрос билета и один дополнительный вопрос.
5.8. Студент Иванов знает только 10 экзаменационных билетов из 25. В каком случае шансы Иванова сдать экзамены выше: когда он берет билет первым или вторым?
5.9. В первой урне лежат 8 белых и 12 черных шаров, во второй урне - 4 белых и 15 черных шаров. Из первой урны во вторую перекладывается один шар, затем из второй урны извлекается шар. Какова вероятность того, что извлеченный шар белый?
5.10. В первой урне находится 3 белых и 7 черных шаров, во второй урне- 5 белых и 3 черных шара. Из первой урны во вторую перекладываются 2 шара, а затем из второй урны извлекается шар. Какова вероятность того, что он белый?
5.11. В ящике лежат 15 новых и 5 игранных теннисных мячей. Для игры наудачу выбираются два мяча, и после игры возвращаются обратно. Затем для второй игры также наудачу отбираются еще два мяча. Какова вероятность того, что вторая игра будет проводиться новыми мячами?
5.12. В первой урне лежат 8 белых и 12 черных шаров, во второй урне - 4 белых и 16 черных шара. Из каждой урны берется по шару и перекладывается в третью урну, затем из третьей урны вытаскивается шар.
Какова вероятность того, что вытащен белый шар?
5.13. В пирамиде 10 винтовок с оптическим прицелом и 20 без оптического прицела. Вероятность попадания в мишень из винтовки с оптическим прицелом равна 0,9, из винтовки без оптического прицела - 0,6.Наугад берется винтовка, и из нее делается выстрел; при этом мишень оказывается пораженной. Найти вероятность того, что выстрел сделан: а) из винтовки с оптическим прицелом; б) из винтовки без оптического
прицела.
5.14. На вход радиолокационного устройства с вероятностью 0,8 поступает смесь полезного сигнала с помехой, а с вероятностью 0,2 – только помеха. Если поступает полезный сигнал с помехой, то устройство регистрирует наличие сигнала с вероятностью 0,7, если только помеха, то с вероятностью 0,3. Известно, что устройство зарегистрировало наличие сигнала. Найти вероятность того, что в его составе есть полезный сигнал.
5.15. Три стрелка стреляют по мишени, которая оказывается пораженной одной пулей. Найти вероятность того, что попал первый стрелок, если вероятности попадания стрелков равны соответственно 0,6, 0,7, 0,8.
ФОРМУЛА БЕРНУЛЛИ
Опыты называются независимыми, если вероятность исхода каждого опыта не зависит от того, какие исходы имели предшествующие опыты. Если производится n независимых опытов в одинаковых условиях, причем в каждом из них событие А появляется с вероятностью p, то вероятность появления в этих опытах события А ровно k раз находится по формуле Бернулли
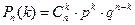 , где q= 1 -p, k =0,1,…, n. (6.1)
, где q= 1 -p, k =0,1,…, n. (6.1)
Вероятность того, что частота m появлений события А в n в испытаниях примет значение из промежутка 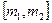 равна
равна
 (6.2)
(6.2)
Вероятность того, что событие А хотя бы один раз наступит в n испытаниях вычисляется по формуле
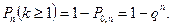 (6.3)
(6.3)
Число  появления события называется наивероятнейшим, если вероятность появления события k раз при n испытаниях превышает (или, по крайней мере, не меньше) вероятности остальных возможных исходов испытаний. Наивероятнейшее число k 0 определяется из двойного неравенства
появления события называется наивероятнейшим, если вероятность появления события k раз при n испытаниях превышает (или, по крайней мере, не меньше) вероятности остальных возможных исходов испытаний. Наивероятнейшее число k 0 определяется из двойного неравенства
(n + 1) p − 1 ≤  ≤ (n + 1) p. (6.4)
≤ (n + 1) p. (6.4)
В том случае, когда вероятность появления события изменяется от опыта к опыту, формула Бернулли (6.1) оказывается неприменимой; в этом случае используется так называемая производящая функция
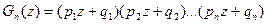 , (6.5)
, (6.5)
где 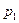 - вероятность появления события А в первом опыте,
- вероятность появления события А в первом опыте, 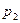 - во втором опыте,...,
- во втором опыте,...,  - в n -oм опыте,
- в n -oм опыте,  = 1 −
= 1 − 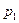 ,
, 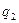 = 1 −
= 1 − 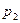 ,...,
,..., 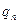 = 1 −
= 1 −  .
.
Тогда вероятность  (k) появления события А ровно k раз равна коэффициенту при
(k) появления события А ровно k раз равна коэффициенту при  в разложении производящей функции
в разложении производящей функции 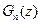 по степеням z.
по степеням z.
Если же результатом каждого опыта является не два исхода 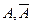 , а несколько взаимно исключающих друг друга исходов:
, а несколько взаимно исключающих друг друга исходов: 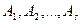 , которые в результате опыта могут появиться с вероятностями
, которые в результате опыта могут появиться с вероятностями  соответственно, то вероятность того, что в n опытах событие
соответственно, то вероятность того, что в n опытах событие  появится
появится 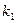 раз, событие
раз, событие  −
− 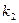 раз,..., событие
раз,..., событие 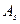 −
−  раз находится по формуле
раз находится по формуле
 . (6.6)
. (6.6)
Отметим, что формула Бернулли (6.1) является частным случаем формулы
(6.6) при s=2.
Пример 1. Вероятность выигрыша лотерейного билета составляет 0,1. Некто покупает 5 лотерейных билетов. Найти вероятности следующих событий: A = {ровно два билета выигрывают}, B = {большая часть билетов выигрывает}, C ={выигрывает хотя бы два билета}.
Решение. Согласно условию задачи  По формуле (6.1)
По формуле (6.1)

Так как событие В означает, что выигрывают 3, 4 или все 5 билетов, то
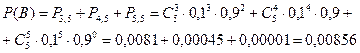
Для вычисления Р(С) перейдем к противоположному событию 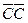 ={выигрывает менее двух билетов}. Так как событие
={выигрывает менее двух билетов}. Так как событие 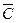 означает, что выигрывает либо 0, либо 1 билет, то
означает, что выигрывает либо 0, либо 1 билет, то
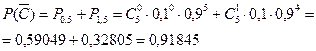
Тогда P(C) = 1 − P(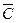 ) = 0,08146.
) = 0,08146.
Ответ: 0,0729; 0,00856; 0,08146.
Пример 2. Испытывается каждый из 15 элементов некоторого устройства. Вероятность выдержать испытание для каждого элемента составляет 0,9. Найти наивероятнейшее число выдержавших испытание элементов и его вероятность.
Решение. Так как n = 15, p = 0,9, то по формуле (6.4) имеем
16 ⋅ 0,9 − 1 ≤  ≤ 16 ⋅ 0,9, откуда
≤ 16 ⋅ 0,9, откуда  = 14.
= 14.
Далее находим 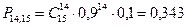
Ответ: 14; 0,343.
Пример 3. Устройство состоит из трех независимо работающих блоков. Вероятности безотказной работы блоков за время t равны соответственно 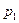 = 0,7,
= 0,7, 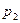 = 0,8,
= 0,8,  = 0,9. Найти вероятности того, что за время t будут работать безотказно: а) все три элемента; б) два элемента; в) один элемент.
= 0,9. Найти вероятности того, что за время t будут работать безотказно: а) все три элемента; б) два элемента; в) один элемент.
Решение. Вероятности отказов блоков равны соответственно 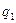 = 0,3,
= 0,3, 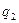 = 0,2,
= 0,2,
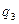 = 0,1. Производящая функция (6.5) для нашей задачи имеет вид
= 0,1. Производящая функция (6.5) для нашей задачи имеет вид

Вероятность безотказной работы всех трех элементов равна коэффициенту при 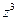 , значит,
, значит,  (3) = 0,504. б) Вероятность безотказной работы двух элементов равна коэффициенту при
(3) = 0,504. б) Вероятность безотказной работы двух элементов равна коэффициенту при 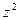 , значит,
, значит,  (2) = 0,398. Вероятность безотказной работы одного элемента равна коэффициенту при z, значит,
(2) = 0,398. Вероятность безотказной работы одного элемента равна коэффициенту при z, значит,  (1) = 0,092.
(1) = 0,092.
Ответ: 0,504; 0,398; 0,092.
Пример 4. В цех по ремонту радиоаппаратуры поступают резисторы с трех заводов в отношении 2:3:5. Мастер для ремонта прибора взял наугад 6 резисторов. Какова вероятность того, что взят 1 резистор первого завода, 2 резистора второго завода, 3 резистора третьего завода?
Решение. Вероятности взять резисторы первого, второго, третьего заводов равны соответственно 0,2, 0,3, 0,5. Используем формулу (6.6), в которой полагаем n = 6, 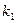 = 1,
= 1, 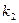 = 2,
= 2, 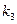 = 3,
= 3, 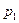 = 0,2,
= 0,2,  = 0,3,
= 0,3,  = 0,5. Получаем
= 0,5. Получаем
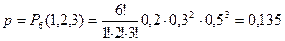
Ответ: 0,135.
6.1. Монета бросается 5 раз. Найти вероятность того, что герб появится: а) 1 раз; б) 2 раза; в) 3 раза.
6.2. Игральная кость бросается 5 раз. Найти вероятность того, что 2 раза появится число очков, кратное трем.
6.3. На цель сбрасывается 6 бомб, вероятность попадания каждой в цель составляет 0,3. Найти вероятность поражения цели: а) 4 бомбами; б) 3 бомбами.
6.4. Вероятность попадания бомбы в цель составляет 0,25. Сбрасывается 8 бомб. Найти вероятность того, что будет: а) не менее 7 попаданий; б) не менее 1 попадания.
6.5. Вероятность попадания стрелком в мишень при каждом выстреле не зависит от результатов предыдущих выстрелов и равна 0,8. Стрелок сделал 5 выстрелов. Найти вероятности следующих событий: а) мишень поражена одной пулей; б) мишень поражена двумя пулями; в) зарегистрировано хотя бы одно попадание; г) зарегистрировано не менее трех попаданий.
6.6. В семье 5 детей; вероятность рождения мальчика равна 0,51. Найти вероятности событий: A = {в семье два мальчика}, B = {в семьене более двух мальчиков}, C = {в семье более двух мальчиков}, D = {в семье не менее 2 и не более 3 мальчиков}.
6.7. Играют две равносильные команды в футбол. В ходе матча забито 4 мяча. Какова вероятность того, что счет будет равным?
6.8. Два равносильных противника играют в шахматы. Что вероятнее: а) выиграть одну партию из двух или две из четырех? б) выиграть не менее двух партий из четырех или не менее трех из пяти? Ничьи во внимание не принимаются.
6.9. ОТК проверяет партию изделий из 10 деталей. Вероятность того, что деталь стандартна, равна 0,75. Найти наивероятнейшее число деталей, которые будут признаны стандартными.
6.10. Игральная кость подбрасывается 16 раз. Найти наивероятнейшее число выпадений очков, кратных 3.