В.Н. Денисов, В.И.Бобков,
Е.И.Выборнова, Н.Ф. Кулага
МАТЕМАТИКА
УЧЕБНЫЙ ПРАКТИКУМ
И контрольные задания
Для студентов заочной формы обучения
Семестр
Смоленск 2010
ВВЕДЕНИЕ
Материал данного пособия предназначен студентам первого курса заочной формы обучения СФ «МЭИ(ТУ)». В данном пособии приведены рекомендации по изучению теоретического материала, примеры решения задач, задачи расчетного задания.
В рекомендациях по изучению теоретического материала указана литература и разделы, соответствующие разделам учебной программы.
В других разделах пособия приведены примеры решениях типовых задач, задачи расчетного задания.
При изучении материала студентам вначале нужно проработать его теоретическую часть по лекциям и указанной в рекомендациях литературе. Затем разобрать приведенные в лекциях и рекомендованной литературе примеры на закрепление теоретического материала. После решить задачи расчетного задания и подготовиться к его защите.
РЕКОМЕНДАЦИИ ПО ИЗУЧЕНИЮ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА.
Программа курса для первого семестра обучения состоит из следующих разделов:
| Матрицы, действия над ними. Алгебра матриц. |
| Определители, их свойства. Миноры. Алгебраические дополнения. Разложение определителя по строке и столбцу. Метод Гаусса. |
| Обратная матрица, ee свойства. Ранг матрицы, его свойства. Матричные уравнения. |
| Системы линейных алгебраических уравнений. Правило Крамера. Теорема Кронеккера-Капелли. |
| Однородные системы. Структура общего решения неоднородной системы. |
| Таблица межотраслевого баланса, модель Леонтьева . |
| Собственные числа и собственные векторы квадратных матриц. |
| Векторы, действия над ними, базис, координаты. Линейная зависимость и независимость векторов. |
| Скалярное, векторное и смешанное произведения векторов. |
| Плоскость и прямая и в пространстве. Различные способы задания прямой и плоскости в пространстве. Расстояние от точки до плоскости. Углы между прямыми и плоскостями. |
| Кривые второго порядка на плоскости, классификация кривых. Канонические уравнения эллипса, параболы, гиперболы. |
| Поверхности второго порядка. Канонические уравнения поверхностей второго порядка. |
| Понятие функции, способы задания функции. Понятие и определение предела функции в точке. |
| Свойства функций, имеющих предел. Бесконечно малые и бесконечно большие функции, их свойства и сравнение. Эквивалентные функции. |
| Непрерывность функции в точке. Свойства непрерывных функций. Классификация разрывов. Функции, непрерывные на отрезке. Последовательности. |
| Дифференцируемость функции в точке. Дифференциал и производная функции, их геометрический смысл. Производная суммы, произведения и частного. |
| Производная сложной функции, обратной функции. Производные и дифференциалы высших порядков. Формула Лейбница. Теоремы о среднем для дифференцируемых функций, правило Лопиталя. Формула Тейлора. |
| Возрастание (убывание) функций. Экстремумы функций. Необходимое условие экстремума, достаточное условие экстремума. Выпуклость, точки перегиба, условия их существования. Общая схема исследования функции с построением графика. |
| Функции нескольких переменных |
Изучение материала курса полезно проводить, придерживаясь тем и рекомендуемой литературы.
1.ТЕМА.
Матрицы, определители, системы линейных уравнений.
После изучения раздела студент должен знать: определение матрицы, типы матриц (квадратные, прямоугольные, единичные), операции над матрицами, определители матриц и их свойства, системы линейных уравнений и методы их решения (правило Крамера, метод Гаусса, метод обращения матриц).
Литература:[1,2].
2.ТЕМА.
Векторы, действия над ними, скалярное, векторное, смешанное произведения. Плоскость, прямая, кривые второго порядка, квадратичные формы.
ЗНАТЬ: понятие вектора, операции над векторами, разные типы произведений векторов, разные виды уравнений прямой, плоскости, канонические уравнения кривых второго порядка.
Литература:[1,2].
3.ТЕМА.
Понятие множества и функции, примеры множеств (натуральные, целые, рациональные и иррациональные числа) и функции (элементарные функции). Понятие предела функции в точке и непрерывности функции в точке.
ЗНАТЬ: символику для работы с множествами, графики основных элементарных функций, геометрический смысл предела функции, определение предела, его свойства и методы нахождения, непрерывность в точке и точки разрыва.
Литература:[1,2].
4.ТЕМА.
Понятие производной функции в точке, ее геометрический и экономический смысл. Вычисление производных при помощи таблицы. Дифференцируемость и дифференциал. Правило Лопиталя. Высшие производные. Исследование функций. Построение графиков.
ЗНАТЬ: таблицу производных, физический и геометрический смысл производной, уметь вычислять производные при помощи таблицы и свойств, исследовать функции и строить графики.
Литература:[1,2].
5.ТЕМА.
Функции нескольких переменных, их производные. Основные теоремы.
Задачи на экстремум.
Литература:[1,2].
ПРИМЕРЫРЕШЕНИЯ ЗАДАЧ.
Расчетное задание состоит из десяти заданий. Для выполнения расчетного задания будут полезны образцы решения задач, приведенные ниже.
Задание 1. Даны матрицы 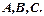
Найти определитель матрицы 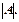
Вычислить результирующую матрицу 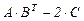 .
.
Образец решения задания.
Пусть
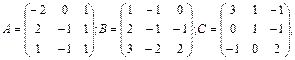
Вычислим определитель матрицы 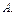 разложением по первой строке:
разложением по первой строке:
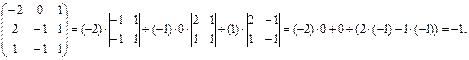
Произведем действия над матрицами с учетом свойств матриц
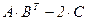 =
=  .
.
После транспонирования матрицы 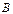 имеем выражение
имеем выражение
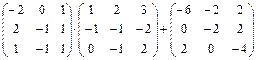 .
.
Перемножая матрицы, получим
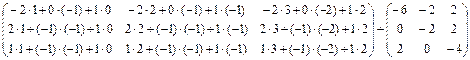
Складывая соответствующие элементы двух полученных матриц, видим, что
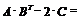
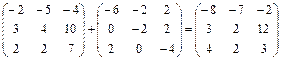 .
.
Задание 2. Решить методом Гаусса и как матричное уравнение систему линейных уравнений.
Суть метода Гаусса состоит в том, что при помощи преобразований, не нарушающих равносильности, исходная система сводится к треугольному виду.
Пример.
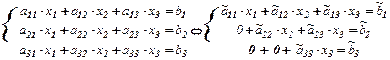
При решении систем методом исключения Гаусса вначале составим расширенную матрицу системы уравнений.
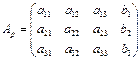 .
.
Преобразуем при помощи метода исключения Гаусса к диагональному виду, составляя линейные комбинации строк, чтобы получить нулевые элементы ниже главной диагонали
1шаг
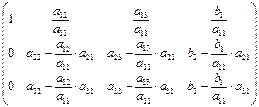
 =
= 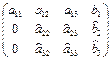 .
.
2 шаг
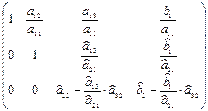
Переход к равносильной треугольной системе называют прямым ходом метода Гаусса. Выражая из треугольной системы 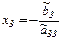 , затем
, затем 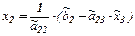 , затем
, затем 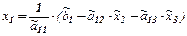 , то есть, выполняя обратный ход метода Гаусса, легко находим решение системы.
, то есть, выполняя обратный ход метода Гаусса, легко находим решение системы.
Равносильные преобразования в методе Гаусса - это линейные комбинации строк матрицы.
Для иллюстрации метода Гаусса рассмотрим примеры.
Пример.
Решить систему уравнений:
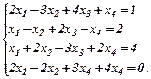
Шаг 1. Делим коэффициенты первого уравнения на коэффициент а11¹0, при этом получается равносильная система уравнений.
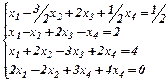
Шаг 2. На месте 2 и 3 уравнений поставим сумму 1-го уравнения, умноженного на (-1), и 2,3- уравнений. На месте 4-го уравнения сумму 1-ой строки, умноженную на (-2), и 4-ой строки. Для краткости записей воспользуемся понятием расширенной матрицы и эквивалентных преобразований
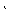
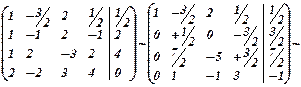
Т. к. во 2, 3, 4 уравнениях неизвестное х1 - исключено, то применим схему приведенную выше для исключения неизвестных в системе, состоящей из 2, 3, 4 уравнений. Для этого вторую строку разделим на 1/2, на месте 3, поставим сумму элементов 2 строки, умноженную на (-7/2), и 3-й строки на месте 4-ой строки сумму элементов 2 строки умноженную на (-1) и 4 строки.
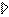
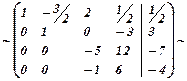
Исключая неизвестные в 3 и 4 уравнениях по той же схеме завершим прямой ход метода Гаусса.
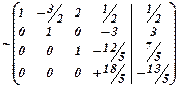
Используя обратный ход метода Гаусса, имеем:
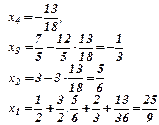 .
.
Если матрица А невырождена (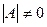 ), то для нее существует обратная матрица, обозначаемая А-1, такая, что А-1×А = А×А-1= Е, где Е – единичная матрица. Используя это свойство, можно решить матричное уравнение так:
), то для нее существует обратная матрица, обозначаемая А-1, такая, что А-1×А = А×А-1= Е, где Е – единичная матрица. Используя это свойство, можно решить матричное уравнение так:
А×Х = В Û А-1×А×Х = А-1×В Û Е×Х = А-1×В,
т.е.
Х = А-1×В
В том случае, когда матричное уравнение имеет вид  A X×C = B, то схема решения такова:
A X×C = B, то схема решения такова:
А-1× А× Х× C× C-1 = А-1× В×C-1 Û Х = А-1× В×C-1
Пример.
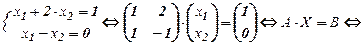
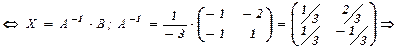
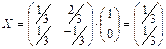
Задание 3. Треугольник ABC задан координатами его вершин: A(-2,1,3), B(1,-2,-3), C(2,-3,-1).
Найти
1). Площадь треугольника ABC;
2). Косинусы углов треугольника;
3). Высоту, опущенную из вершины А на сторону ВС;
4). Определить, параллелен ли вектор плоскости треугольника АВС.
Решение.
Найдем координаты векторов АВ=(1+2,-2-1,-3-3)=(3,-3,-6), АС=(4,-4,-4), ВС=(1,-1,2). Так как площадь треугольника равна половине площади соответствующего параллелограмма, то, используя геометрический смысл векторного произведения векторов, найдем площадь треугольника как половину модуля векторного произведения векторов, на которых построен треугольник.
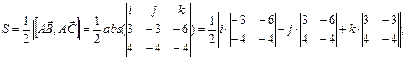
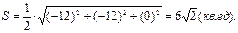
Углы треугольника легко определить, используя скалярное произведение векторов. Например, для угла А имеем
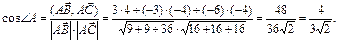
Для отыскания высоты, опущенной из вершины А на сторону ВС, разделим площадь треугольника на длину стороны ВС, т.е. на модуль вектора ВС.
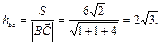
Узнать о параллельности вектора 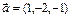 можно при помощи смешанного произведения векторов
можно при помощи смешанного произведения векторов 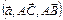 . Если оно равно 0, то векторы компланарны, т.е. лежат в одной плоскости, если не равно 0, то некомпланарны. Найдем смешанное произведение векторов
. Если оно равно 0, то векторы компланарны, т.е. лежат в одной плоскости, если не равно 0, то некомпланарны. Найдем смешанное произведение векторов
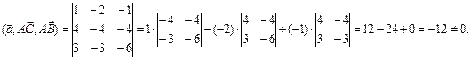
Значит, вектор 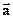 не параллелен плоскости треугольника АВС.
не параллелен плоскости треугольника АВС.
Задание 4. Задана прямая 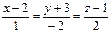 и плоскость
и плоскость 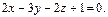
Найти
1). Угол между прямой и плоскостью в градусах, округлив результат до единиц градусов;
2). Точку пересечения прямой и плоскости, если она существует.
Решение.
Угол между прямой и плоскостью можно найти как, дополняющий до прямого, угол между направляющим вектором прямой 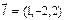 и нормальным вектором плоскости
и нормальным вектором плоскости 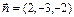 , используя скалярное произведение векторов. Так как
, используя скалярное произведение векторов. Так как
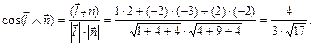
Значит угол равен 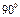 -
- 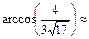
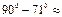
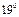 .
.
Для определения точки пересечения прямой и плоскости запишем совместно параметрические уравнения прямой и уравнение плоскости, и решим их путем подстановки первого, второго и третьего выражений в четвертое уравнение. После чего получим
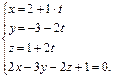
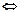
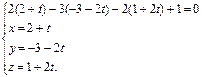
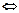
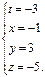
Задание 5. Найти пределы функций
При нахождении пределов функции пользуются следующими свойствами пределов и теоремами:
1).Предел константы равен самой константе.
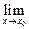 k=k.
k=k.
2). Если существует ($) 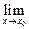 f(x)=А (конечный), $
f(x)=А (конечный), $ 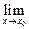 g(x)=B (конечный), то:
g(x)=B (конечный), то:
- предел суммы (разности) этих функций х®х0 существует и равен сумме (разности) пределов
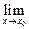 (f(x)
(f(x) 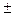 g(x))=
g(x))= 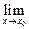 f(x)
f(x) 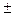
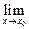 g(x);
g(x);
- предел произведения существует и равен произведению пределов
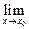 [f(x)×g(x)]=
[f(x)×g(x)]= 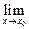 f(x)×
f(x)× 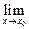 g(x);
g(x);
- предел частного функций существует и равен частному пределов

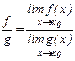 , В¹0.
, В¹0.
3). Пределы основных элементарных функций равны значениям этих функций в точке, где ищется предел. Например
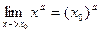 ,
, 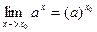 ,
, 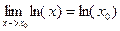 ,
,
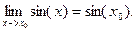
При нахождении пределов нельзя пользоваться рассмотренными выше свойствами, если:
1) f(x)®0, j(x)®0, при x®x0 и ищется предел вида 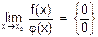 . В этом случае говорят о наличии неопределенности вида ноль делить на ноль
. В этом случае говорят о наличии неопределенности вида ноль делить на ноль 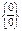 .
.
2) f(x)®0, j(x)®¥, при x®x0, то о пределе вида 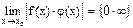 , говорят как об имеющем неопределенность ноль умножить на бесконечность.
, говорят как об имеющем неопределенность ноль умножить на бесконечность.
3) f(x)® +¥, j(x)® +¥, при x®x0, то говорят, что 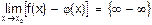 имеет неопределенность вида
имеет неопределенность вида 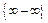 .
.
4) f(x)® ¥, j(x)® ¥, при x®x0, то говорят, что 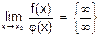 имеет неопределенность бесконечность делить на бесконечность.
имеет неопределенность бесконечность делить на бесконечность.
При нахождении пределов в этих случаях нужно вначале избавиться от неопределенности и лишь после этого применять теоремы и свойства пределов. С этой целью, как правило, выделяют в числителе и знаменателе одинаковые множители, стремящиеся к нулю или к бесконечности, или избавляются от иррациональности умножением на сопряженное выражение или применяют эквивалентные функции.
Пример.
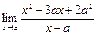 =
= 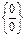 =
= 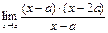 =
= 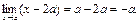
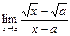 =
=  =
= 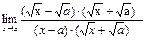 =
=

При нахождении пределов применяют теоремы о связи бесконечно-малых и бесконечно-больших функций и теорему о пределе показательно-степенной функции:
Если y=f(x), при x®x0 бесконечно малая функция(f(x)->0), то [1/f(x)]-> 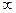 при x®x0 - бесконечно большая функция и наоборот, если j(х)- бесконечно большая функция при x®x0, то [1/j(x)]- бесконечно малая функция при x®x0.
при x®x0 - бесконечно большая функция и наоборот, если j(х)- бесконечно большая функция при x®x0, то [1/j(x)]- бесконечно малая функция при x®x0.
Пример.
Вычислить:
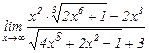 .
.
Порядок роста (наибольший показатель степени у слагаемых) числителя и знаменателя один и тот же и равен 11.
Делим числитель и знаменатель на 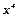 и учитывая связь бесконечно больших и бесконечно малых функций, имеем
и учитывая связь бесконечно больших и бесконечно малых функций, имеем
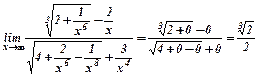 .
.
Если 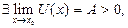 и
и 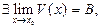 то существует предел показательно-степенной функции, причем
то существует предел показательно-степенной функции, причем 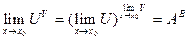 .
.
При этом если
1) 0<A<1; 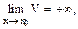
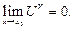
2) A>1; 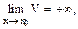
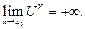
3) 0<A<1, 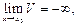
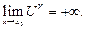
4) A>1, 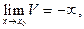
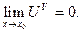
Если же U®1, V®¥, при x®x0, то говорят о неопределенности вида {1 ¥}:
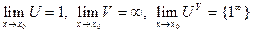 неопределенность.
неопределенность.
Для раскрытия неопределенности такого вида применяется формула
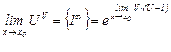 .
.
Примеры:
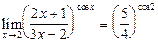 ,
,
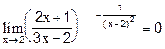 .
.
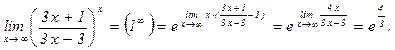
Задание 6. Найти производную заданной функции.
При нахождении производных функции в точке и на интервале применяют таблицу производных, их свойства и теоремы о производных.
Таблица производных:
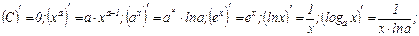
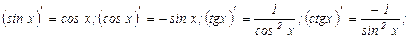
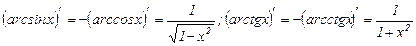
Свойства производных. 
Если существуют производные функций 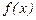 и
и 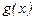 в точках
в точках 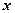 интервала
интервала 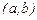 , а
, а 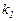 и
и 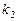 постоянные множители, то:
постоянные множители, то:
1. Производная суммы (разности) функций равна сумме (разности) производных, константы можно выносить за знак производной, при этом справедлива формула:
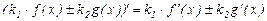 .
.
Пример.
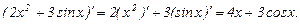
2. Производная произведения вычисляется по формуле:
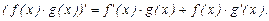
Пример.
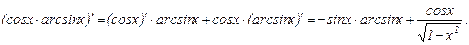
3. Производная частного (дроби) вычисляется по формуле:
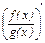 =
= 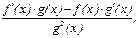
Пример.
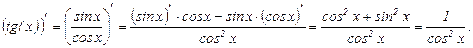
Пример.
Найти 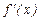 , если
, если 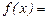
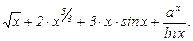 Используя свойство производной суммы и переходя от арифметических корней к степенным функциям, имеем
Используя свойство производной суммы и переходя от арифметических корней к степенным функциям, имеем
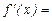

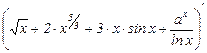 =
=
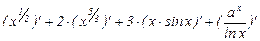 .
.
Применяя таблицу производных и формулы для дифференцирования произведения и частного, получим
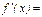
= 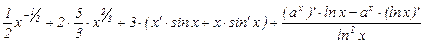 =
=
= 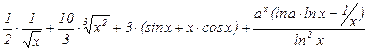 .
.
При нахождении производных часто применяется следующая теорема.