Определение.
Функция z=f(x,y), называется дифференцируемой в точке М0(x0,y0), если ее приращение Dz=ADx+BDy+a(Dx,Dy), где a(Dx,Dy)®0, при (Dx,Dy)®(0,0). При этом A,B- константы в точке М0, Dz=f(x0+Dx, y0+Dy)-f(x0,y0) - полное приращение функции.
Определение.
Дифференциалом функции z=f(x,y) называют выражение dz=Adx+Bdy- линейную часть приращения функции z=f(x,y) в т. М0.
Теорема. Необходимое условие дифференцируемости.
Если z=f(x,y) дифференцируема в т. М0, то она непрерывна в этой точке.
Доказательство.
Т.к. z=f(x,y) дифференцируема в т. М0 Þ Dz=ADx+BDy+a(Dx,Dy), тогда
 т. е.
т. е.
z=f(x,y) непрерывна по определению.
Теорема. О связи дифференциала и производных.
Если z=f(x,y) дифференцируема в т. М0 (x0,y0), тогда существуют  и
и  .
.
Доказательство.
Из дифференцируемости следует, что Dz=ADx+BDy+a(Dx,Dy), но тогда
при y=0 Dxz=ADx+a(Dx,0) Þ  =A,
=A,
при Dx=0 Dyz=BDy+a(0,Dy) Þ  =B.
=B.
Что и требовалось доказать. При этом дифференциал имеет вид
dz=z'xdx+z'ydy
Теорема. Достаточное условие дифференцируемости ФМП.
Если $z'x и z'y- непрерывные в т. М0, то функция z=f(x,y) дифференцируема в т. М0.
так как dz=z-z0=z'x(x-x0)+z'y(y-y0), то геометрический смысл дифференциала - приращение в т. М0 аппликаты z- касательной плоскости к графику функции z=f(x,y).
Сложные ФМП
Определение.
Если z=f(x,y) определена на "(x,y)ÎD и имеют смысл функции x=x(u,v), y=y(u,v), "(u,v)ÎD, то говорят, что задана сложная ФМП z=f(x(u,v), y(u,v)).
Пример.
z=ln(cos(x×y)+tg(x+y))=ln (cosu+tgv),  ,
,
При нахождении частных производных ФМП применяют следующие теоремы.
Теорема. О производной сложной функции.
Если z=f(x,y) дифференцируема для " пар (x,y)ÎD и
$x't,y't для tÎ[a,b], то производная может быть вычислена по формуле 
Доказательство. Из дифференцируемости z=f(x,y) следует Dz=  . Так как $ x't,y't,то x(t) и y(t)- непрерывные, значит Dx®0, Dy®0, при Dt®0, а тогда
. Так как $ x't,y't,то x(t) и y(t)- непрерывные, значит Dx®0, Dy®0, при Dt®0, а тогда  , Dt¹0.
, Dt¹0.
Переходя к пределу имеем

Теорема. О производной z=f(x(u,v), y(u,v))
Если z=f(x,y) дифференцируема для "(x,y)ÎD и $  ,
,  ,
,  ,
,  для "(u,v)ÎD, тогда справедливы формулы
для "(u,v)ÎD, тогда справедливы формулы

Частные производные и дифференциалы высших порядков.
Если существуют первые производные от частных производных найденных ранее, то они называются частными производными высших порядков и обозначаются
если $ 
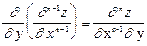

 .
.
Аналогично первые дифференциалы от дифференциалов, найденных ранее, если dx и dy фиксированы, называют дифференциалами высших порядков и обозначают
d(dn-1z)  dnz, d2z=f''xx(dx)2+2f''xydxdy+f''yy(dy)2.
dnz, d2z=f''xx(dx)2+2f''xydxdy+f''yy(dy)2.
Пример.
Если z=x2y+xy2, то
f'x=2xy+y2, f'y=x2+2xy Þ f''xx=2y, f''yy=2x, f''xy=2x+2y.
Тогда d2z=2ydx2+4(x+y)2xdy+2xdy2.
Заметим, что как и для функции одной переменной дифференциал dz=f'xdx+f'ydy- обладает свойством инвариантности, дифференциалы более высоких порядков- нет.
Экстремумы ФНП
Определение.
Точка М0- точка максимума (минимума) функции z=f(x,y), если $d- окрестность т. М0 такая, что для "(x,y)из этой окрестности f(x,y)<f(x0,y0) (f(x,y)>f(x0,y0)

Теорема. Необходимое условие экстремума.
Если т. М0 (x0,y0)- точка экстремума, тогда или
 или
или 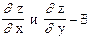 (не существуют).
(не существуют).
В дальнейшем точки в которых z'x=0 и z'y=0 или не $ назовем критическими.
Теорема. Достаточное условие экстремума.
Пусть т. М0- критическая, причем
z=f(x,y)- непрерывна в т. М0
существуют f''xx, f''yy, f''xy в т. М0, тогда
при D(M0)=f''xx(M0)f''yy(M0)-[f''xy(M0)]2 >0, экстремум есть, причем при f''x(M0)<0- максимум, f''yy(M0)>0- минимум.
Если же D<0, экстремума нет, при D=0- ничего нельзя сказать о наличии экстремума.
Пример.
z=x2+y2 Þ 
Так как D(М0)=2×2-0>0- экстремум есть, причем z''xx>0 Þ в точке М0-минимум.
Если требуется найти экстремум функции z=f(x,y) при условии, что переменные x,y связаны условием g(x,y)=0, то задачи такого вида называют задачами на условный экстремум и решают методом множителей Лангража.
Метод множителей Лагранжа.
Пусть требуется найти условный экстремум функции
z=f(x,y)
при наличии условия
g(x,y)=0.
Идея метода Лагранжа состоит в том, что:
1. Вводится новая функция трех переменных, называемая функцией Лангража как
F(x,y,l)=f(x,y)+lg(x,y),
где l- неопределенный множитель, который рассматривается как новая переменная;
2. Ищется экстремум (уже безусловный) этой функции. Для этого вычисляются частные производные первого порядка и приравниваются к нулю:

Полученные уравнения образуют систему трех уравнений с тремя неизвестными. Решение этой системы представляет собой тройку чисел (x0, y0, l0), первые два из которых, т. е. (x0,y0), и дают координаты точки условного экстремума исходной функции f(x,y).
Применим метод Лагранжа для отыскания экстремума функций [1].
Пример.
Пусть f(x,y)=x2-3xy+12x при условии g(x,y)=6-2x-3y=0.
Функция Лангража имеет вид F(x,y,l)=x2 - 3xy+12x+l(2x+3y-6).
Тогда F'x(x,y,l)=2x-3y+12+2l,
F'y(x,y,l)=-3x+3l,
F'l(x,y,l)=-6+2x+3y=0.
Приравняв к нулю получим систему

Решим полученную систему методом исключения. Для этого умножим первое (сверху) уравнение на 3, а второе на -2 и складываем, третье уравнение вычитаем из первого. Этим исключается переменная х и система принимает вид:

Теперь исключаем переменную l, умножая второе уравнение на -6, и складывая с первым. В результате
-27y=72ÞY=8/3.
Подставляя это значение в уравнение, находим сначала l, затем х:
l=-1; x=-1.
Значит координаты точки условного экстремума (-1, 8/3). Соответствующее значение функции
f(-1, 8/3)=(-1)2×-3×(-1)×(8/3)+12×(-1)=-3.
4. Расчетное задание
Задание 1. Даны матрицы  Найти определитель матрицы
Найти определитель матрицы 
Вычислить результирующую матрицу 
1.1 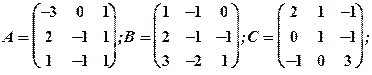
1.2 
1.3 
1.4 
1.5 
1.6 
1.7 
1.8 
1.9 
1.10 
1.11 
1.12 
1.13 
1.14 
1.15 
1.16 
1.17 
1.18 
1.19 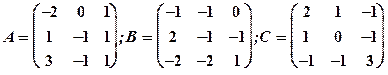
1.20 
1.21 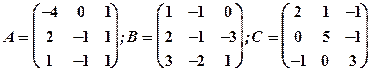
1.22 
1.23 
1.24 
1.25 
1.26 
1.27 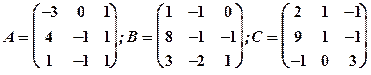
1.28 
1.29 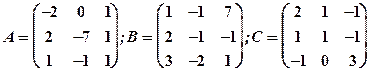
1.30 
1.31 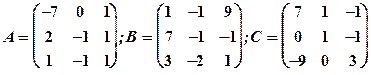
1.32 
Задание 2. Решить методом Гаусса и как матричное уравнение следующую систему линейных уравнений.


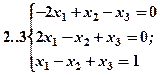








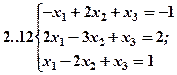












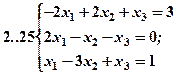







Задание 3. Треугольник ABC задан координатами его вершин: A(-2,1,3), B(1,-2,-3), C(2,-3,-1).
Найти
1). Площадь треугольника ABC;
2). Косинусы углов треугольника;
3). Высоту, опущенную из вершины А на сторону ВС;
4). Определить, параллелен ли вектор  плоскости треугольника АВС.
плоскости треугольника АВС.
Условия задач.
3.1 A(-2,1,4), B(-1,-2,-3), C(3,-3,-1),  3.2 A(0,3,5), B(1,-2,-3), C(2,-3,-1)
3.2 A(0,3,5), B(1,-2,-3), C(2,-3,-1) 
3.3 A(-2,1,3), B(3,-2,-4), C(2,-3,-1)  3.4 A(-2,4,3), B(-1,-2,-3), C(2,-3,-1)
3.4 A(-2,4,3), B(-1,-2,-3), C(2,-3,-1) 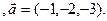
3.5 A(-2,1,3), B(5,-2,-3), C(2,-3,-1)  3.6 A(-2,1,3), B(1,-2,-3), C(6,-3,-1)
3.6 A(-2,1,3), B(1,-2,-3), C(6,-3,-1) 
3. 7 A(-2,1,4), B(1,-2,-3), C(2,-3,-1) 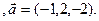 3.8 A(-2,-5,3), B(1,-2,-3), C(2,-3,-1)
3.8 A(-2,-5,3), B(1,-2,-3), C(2,-3,-1) 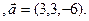
3.9 A(-2,1,3), B(1,-2,-3), C(-2,-3,-1)  3.10 A(-2,-2,3), B(1,-2,-3), C(2,-3,-1)
3.10 A(-2,-2,3), B(1,-2,-3), C(2,-3,-1) 
3.11 A(-2,1,3), B(1,-2,-3), C(8,-3,-1)  3.12 A(-2,1,3), B(1,-2,-3), C(3,-3,-1)
3.12 A(-2,1,3), B(1,-2,-3), C(3,-3,-1) 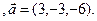
3.13 A(-2,1,5), B(1,-2,-3), C(2,-3,-1) 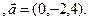 3.14 A(-2,7,3), B(1,-2,-3), C(2,-3,-1)
3.14 A(-2,7,3), B(1,-2,-3), C(2,-3,-1) 
3.15 A(-2,1,3), B(1,-2,-3), C(2,-3,-5)  3.16 A(-2,1,3), B(1,-2,3), C(2,-3,-5)
3.16 A(-2,1,3), B(1,-2,3), C(2,-3,-5) 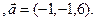
3.17 A(-2,1,3), B(1,-2,-3), C(-3,-3,-1)  3.18 A(-2,4,3), B(1,-2,-3), C(2,-3,-1)
3.18 A(-2,4,3), B(1,-2,-3), C(2,-3,-1) 
3.19 A(-2,5,3), B(1,-2,-3), C(2,-3,-1)  3.20 A(-2,7,3), B(1,-2,-3), C(2,-3,-1)
3.20 A(-2,7,3), B(1,-2,-3), C(2,-3,-1) 
3.21 A(-2,1,-3), B(1,-2,-3), C(2,-3,-1)  3.22 A(-2,1,3), B(1,-2,-3), C(5,-3,-1)
3.22 A(-2,1,3), B(1,-2,-3), C(5,-3,-1) 
3.23 A(-2,1,3), B(1,-2,-3), C(7,-3,-1)  3.24 A(-2,1,5), B(1,-2,-3), C(2,-3,-1)
3.24 A(-2,1,5), B(1,-2,-3), C(2,-3,-1) 
3.25 A(-2,1,1), B(1,-2,-3), C(5,-3,-1)  3.26 A(-2,1,-3), B(1,-2,-3), C(5,-3,-1)
3.26 A(-2,1,-3), B(1,-2,-3), C(5,-3,-1) 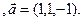
3.27 A(-2,1,-3), B(1,-5,-3), C(2,-3,-1) 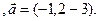 3.28 A(-2,1,5), B(1,-2,-3), C(3,-3,-1)
3.28 A(-2,1,5), B(1,-2,-3), C(3,-3,-1)  .
.
3.29 A(-2,1,3), B(-1,-2,-3), C(2,-7,-1)  3.30 A(-2,5,3), B(1,-2,-3), C(7,-3,-1)
3.30 A(-2,5,3), B(1,-2,-3), C(7,-3,-1) 
3.31 A(-2,1,1), B(5,-2,-3), C(2,-3,-1)  3.32 A(-2,0,3), B(1,-2,-3), C(5,-3,-1)
3.32 A(-2,0,3), B(1,-2,-3), C(5,-3,-1) 
Задание 4.
Задана прямая  и плоскость
и плоскость 
Найти
1). Угол между прямой и плоскостью в градусах, округлив результат до единиц градусов;
2). Точку пересечения прямой и плоскости, если она существует.
4.1  ,
, 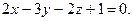
4.2  ,
, 
4.3  ,
, 
4.4  ,
, 
4.5  ,
,  4.6
4.6  ,
, 
4.7 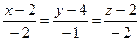 ,
, 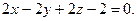 4.8
4.8  ,
, 
4.9  ,
,  4.10
4.10  ,
, 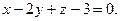
4.11  ,
,  4.12
4.12  ,
, 
4.13  ,
,  4.14
4.14  ,
, 
4.15  ,
,  4.16
4.16  ,
, 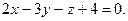
4.17  ,
,  4.18
4.18  ,
, 
4.19  ,
,  4.20
4.20  ,
, 
4.21  ,
,  4.22
4.22  ,
, 
4.23  ,
,  4.24
4.24  ,
, 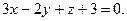
4.25  ,
, 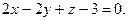 4.26
4.26  ,
, 
4.27  ,
,  4.28
4.28  ,
, 
4.29  ,
,  4.30
4.30  ,
, 
4.31  ,
, 
4.32  ,
, 
Задание 5. Найти пределы функций.
5.1 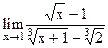 ;
;  . 5.16
. 5.16  ;
; 
5.2  ;
;  . 5.17
. 5.17  ;
; 
5.3  ;
;  . 5.18
. 5.18  ;
; 
5.4  ;
;  . 5.19
. 5.19 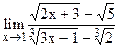 ;
; 
5.5  ;
;  . 5.20
. 5.20  ;
; 
5.6  ;
;  . 5.21
. 5.21  ;
; 
5.7  ;
; 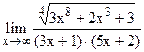 . 5.22
. 5.22  ;
; 
5.8  ;
;  . 5.23
. 5.23  ;
; 
5.9  ;
;  . 5.24
. 5.24 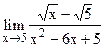 ;
; 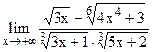
5.10 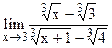 ;
; 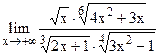 . 5.25
. 5.25  ;
; 
5.11  ;
;  . 5.26
. 5.26  ;
; 
5.12  ;
;  . 5.27
. 5.27  ;
; 
5.13  ;
;  . 5.28
. 5.28  ;
; 
5.14  ;
;  . 5.29
. 5.29  ;
; 
5.15  ;
; 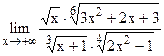 . 5.30
. 5.30  ;
; 
Задание 6. Найти первую производную заданной функции.

3.1 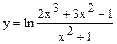 3.2
3.2 
3.3 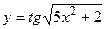 3.4
3.4 
3.5 
 3.6
3.6 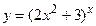
3.7  3.8
3.8 
3.9  3.10
3.10 
3.11  3.12
3.12 
3.13  3.14
3.14 
3.15 
 3.16
3.16 
3.17  3.18
3.18 
3.19 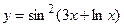 3.20
3.20 
3.21 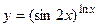 3.22
3.22 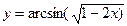
3.23  3.24
3.24 
3.25  3.26
3.26 
3.27  3.28
3.28 
3.29  3.30
3.30 
Задание 7.
Найти производную указанного порядка при помощи формулы Лейбница.
7.1  ; 7.2
; 7.2 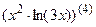 ;
;
7.3  ; 7.4
; 7.4  ;
;
7.5  ; 7.6
; 7.6  ;
;
7.7  ; 7.8
; 7.8  ;
;
7.9  ; 7.10
; 7.10  ;
;
7.11  ; 7.12
; 7.12  ;
;
7.13  ; 7.14
; 7.14  ;
;
7.15  ; 7.16
; 7.16  ;
;
7.17  ; 7.18
; 7.18  ;
;
7.19  ; 7.20
; 7.20  ;
;
7.21  ; 7.22
; 7.22 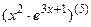 ;
;
7.23  ; 7.24
; 7.24  ;
;
7.25  ; 7.26
; 7.26  ;
;
7.27  ; 7.28
; 7.28  ;
;
7.29  ; 7.30
; 7.30  ;
;
8. Построить график функции при помощи первой производной.
8.1 
 8.2
8.2 

8.3 
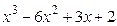 8.4
8.4 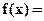

8.5 
 8.6
8.6 

8.7 
 8.8
8.8 

8.9 
 8.10
8.10 

8.11 
 8.12
8.12 

8.13 
 8.14
8.14 

8.15 
 8.16
8.16 

8.17 
 8.18
8.18 

8.19 
 8.20
8.20 

8.21 
 8.22
8.22 

8.23 
 8.24
8.24 

8.25 
 8.26
8.26 

8.27 
 8.28
8.28 

8.29 
 8.30
8.30 

9. Провести полное исследование функции и построить ее график.
9.1  9.2
9.2 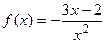
9.3  9.4
9.4 
9.5  9.6
9.6 
9.7  9.8
9.8 
9.9  9.10
9.10 
9.11  9.12
9.12 
9.13 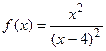 9.14
9.14 
9.15  9.16
9.16 
9.17  9.18
9.18 
9.19  9.20
9.20 
9.21 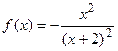 9.22
9.22 
9.23 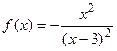 9.24
9.24 
9.25  9.26
9.26 
9.27 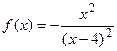 9.28
9.28 
9.29  9.30
9.30 
Задание 10. Найти экстремум функции многих переменных в замкнутой области.
10.1 
10.2 
10.3 
10.4 
10.5 
10.6 
10.7 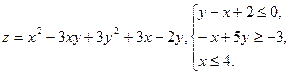
10.8 
10.9 
10.10 
10.11 
10.12 
10.13 
10.14 
10.15 
10.16 
10.17 
10.18 
10.19 
10.20 
10.21 
10.22 
10.23 
10.24 
10.25 
10.26 
10.27 
10.28 
10.29 
10.30 
ЛИТЕРАТУРА:
1.Шипачев В.С. Высшая математика. Учебник для вузов. М.: Высшая школа, 2005.
2. Письменный Д.Т. Конспект лекций по высшей математике. М.: Айрис-Пресс, 2005.
