Теорема( о производной сложной функции).

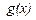Если функция дифференцируема для любых а функция дифференцируема для любых тогда сложная функция дифференцируема для любых и ее производная находится по формуле = .

Пример.

Найти производную сложной функции

, где .

В соответствии с теоремой имеем:

=

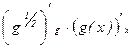
или

= = =

= = .

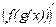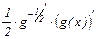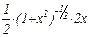При нахождении производной, теорема может применяться несколько раз подряд.

Пример.

Для функции найти производную . Используя формулу из теоремы один раз имеем:

= .

Но функция 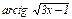тоже сложная. Применив теорему к этой функции, получим

= .

Применяя теорему еще два раза, продолжим цепочку равенств

= = .

Таким образом, при дифференцировании сложной функции находится производная "внешней " функции без учета выражения, являющегося ее аргументом, затем полученная производная умножается на производную выражения, являющегося аргументом.

Для некоторых видов функций применяются специальные приемы нахождения производных.

Если имеется показательно- степенная функция или частное вида , где 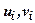- функции, 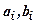- числа, то для нахождения производных этих функций применяется прием логарифмического дифференцирования. Этот прием основан на использовании основного логарифмического тождества , в частности, 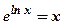, и свойств логарифмов

Суть приема состоит в том, что производную любой функции можно найти как произведение этой функции на производную логарифма ее модуля

.

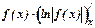С учетом полученной формулы производная показательно-степенной функции равна произведению самой функции на производную логарифма этой функции:

или

Таким образом получена известная формула для производной показательно-степенной функции как сумма производных показательной (при фиксированной 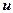) и степенной (при фиксированной ) функций.

Пример.

Пусть . Применяя прием логарифмического дифференцирования, имеем

=

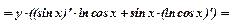
Применяя прием логарифмического дифференцирования для случая дроби, имеем

= =

=

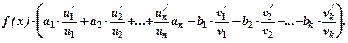
Пример.

Найти производную дроби

Применяя прием логарифмического дифференцирования и свойства логарифмов, видим, что

= =

= .

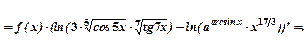
Преобразовав полученное выражение, получим:

Если у функции существовала производная в точке х₀ или на интервале то операция нахождения производной называлась дифференцированием функции. С наличием производной функции в точке тесно связано понятие дифференцируемости функции в точке, которое вводится по определению.

Определение.

Функция называется дифференцируемой в точке х₀, если ее приращение в окрестности этой точки представимо в виде

().

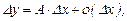Здесь 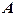- некоторое число, определяемое в точке х₀ . Используя дифференцируемость функции в точке, введем понятие дифференциала функции в точке.

Определение.

Дифференциалом функции в точке x₀ называется линейная часть приращения дифференцируемой функции, при этом вводится обозначение

.

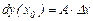Связь между наличием производной и дифференцируемостью функции в точке дается следующей теоремой.