Виды событий.
1. Невозможное(которое не может произойти)
2. Достоверное(событие которое всегда произойдет в результате эксперимента)
Операции.
1 сложение
Суммой событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
2 умножение.
Умножение-наступление всех событий.
3 разность.
Разностью событий называется событие состоящее в том, что наступает событие А, но не наступает событие В.
4 дополнение(отрицание)
Дополнением к событию А называется событие, состоящее в том, что событие А не произошло
Вопрос №6 – классическое, статистическое и геометрическое определение вероятности
Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных исходов опыта в котором может появиться это событие.
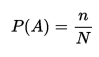
Статистическое (частотное) 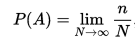
Геометрическое определение 
№7 теоремы сложения вероятностей совместных и не совместных событий. Следствия.
Вероятность суммы не совместных событий равна сумме вероятностей этих событий.
Следствие1
Вероятность суммы событий, образующих полную группу=1.
Следствие2
Сумма вероятностей противоположных событий=1
№8условная вероятность. Теоремы умножения вероятностей.
Условная вероятность -вероятность наступления одного события при условии, что другое событие уже произошло.
Теоремы.
Вероятность произведения двух событий = произведению вероятности одного из них на условную вероятность другого в предположении, что первое событие уже произошло
№9 формула полной вероятности.
№10 формула Байеса. 
Допустим, что произведено какое-либо испытание в результате которого наступило событие А. наступление события привело к изменению вероятностей гипотез эти вероятности позволяют найти формулу Байеса.
№11Формула Бернулли.

Считается что вероятность наступления события постоянна.
№12 формула Пуассона.

Таблица 8. Значения  (распределение Пуассона)
(распределение Пуассона)

| 
| 
| 
| 
| 
| 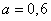
| 
| 
| 
| |
| 0,9018 | 0,8187 | 0,7408 | 0,6703 | 0,6065 | 0,5458 | 0,4966 | 0,4493 | 0,4066 | ||
| 0,0905 | 0,1638 | 0,2222 | 0,2681 | 0,3033 | 0,3293 | 0,3476 | 0,3595 | 0,3659 | ||
| 0,0045 | 0,0164 | 0,0333 | 0,0536 | 0,0758 | 0,0988 | 0,1217 | 0,1438 | 0,1647 | ||
| 0,0002 | 0,0019 | 0,0033 | 0,0072 | 0,0126 | 0,0198 | 0,0284 | 0,0383 | 0,0494 | ||
| 0,0001 | 0,0002 | 0,0007 | 0,0016 | 0,0030 | 0,0050 | 0,0077 | 0,0111 | |||
| 0,0001 | 0,0002 | 0,0004 | 0,0007 | 0,0012 | 0,0020 | |||||
| 0,0001 | 0,0002 | 0,0003 | ||||||||

| 
| 
| 
| 
| 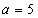
| 
| 
| 
| 
| 
|
| 0,3679 | 0,1353 | 0,0498 | 0,0183 | 0,0067 | 0,0025 | 0,0009 | 0,0003 | 0,0001 | 0,0000 | |
| 0,3679 | 0,2707 | 0,1494 | 0,0733 | 0,0337 | 0,0149 | 0,0064 | 0,0027 | 0,0011 | 0,0005 | |
| 0,1839 | 0,2707 | 0,2240 | 0,1465 | 0,0842 | 0,0446 | 0,0223 | 0,0107 | 0,0050 | 0,0023 | |
| 0,0613 | 0,1804 | 0,2240 | 0,1954 | 0,1404 | 0,0892 | 0,0521 | 0,0286 | 0,0150 | 0,0076 | |
| 0,0153 | 0,0902 | 0,1680 | 0,1954 | 0,1755 | 0,1339 | 0,0912 | 0,0572 | 0,0337 | 0,0189 | |
| 0,0031 | 0,0361 | 0,1008 | 0,1563 | 0,1755 | 0,1606 | 0,1277 | 0,0916 | 0,0607 | 0,0378 | |
| 0,0005 | 0,0120 | 0,0504 | 0,1042 | 0,1462 | 0,1606 | 0,1490 | 0,1221 | 0,0911 | 0,0631 | |
| 0,0001 | 0,0037 | 0,0216 | 0,0595 | 0,1044 | 0,1377 | 0,1490 | 0,1396 | 0,1171 | 0,0901 | |
| 0,0009 | 0,0081 | 0,0298 | 0,0653 | 0,1033 | 0,1304 | 0,1396 | 0,1318 | 0,1126 | ||
| 0,0002 | 0,0027 | 0,0132 | 0,0363 | 0,0688 | 0,1014 | 0,1241 | 0,1318 | 0,1251 | ||
| 0,0008 | 0,0053 | 0,0181 | 0,0413 | 0,0710 | 0,0993 | 0,1186 | 0,1251 | |||
| 0,0002 | 0,0019 | 0,0082 | 0,0225 | 0,0452 | 0,0722 | 0,0970 | 0,1137 | |||
| 0,0001 | 0,0006 | 0,0034 | 0,0126 | 0,0263 | 0,0481 | 0,0728 | 0,0948 | |||
| 0,0002 | 0,0013 | 0,0052 | 0,0142 | 0,0296 | 0,0504 | 0,0729 | ||||
| 0,0001 | 0,0005 | 0,0022 | 0,0071 | 0,0169 | 0,0324 | 0,0521 | ||||
| 0,0002 | 0,0009 | 0,0033 | 0,0090 | 0,0194 | 0,0347 | |||||
| 0,0003 | 0,0014 | 0,0045 | 0,0109 | 0,0217 | ||||||
| 0,0001 | 0,0006 | 0,0021 | 0,0058 | 0,0128 | ||||||
| 0,0002 | 0,0009 | 0,0029 | 0,0071 | |||||||
| 0,0001 | 0,0004 | 0,0014 | 0,0037 | |||||||
| 0,0002 | 0,0006 | 0,0019 | ||||||||
| 0,0001 | 0,0003 | 0,0009 | ||||||||
| 0,0001 | 0,0004 | |||||||||
| 0,0002 | ||||||||||
| 0,0001 |
№13теоремы Муавра-Лапласа.
| 0,0 | 0,3989 | 0,3989 | 0,3989 | 0,3988 | 0,3986 | 0,3984 | 0,3982 | 0,3980 | 0,3977 | 0,3973 |
| 0,1 | 0,3970 | 0,3965 | 0,3961 | 0,3956 | 0,3951 | 0,3945 | 0,3939 | 0,3932 | 0,3925 | 0,3918 |
| 0,2 | 0,3910 | 0,3902 | 0,3894 | 0,3885 | 0,3876 | 0,3867 | 0,3857 | 0,3847 | 0,3836 | 0,3825 |
| 0,3 | 0,3814 | 0,3802 | 0,3790 | 0,3778 | 0,3765 | 0,3752 | 0,3739 | 0,3726 | 0,3712 | 0,3698 |
| 0,4 | 0,3683 | 0,3668 | 0,3652 | 0,3637 | 0,3621 | 0,3605 | 0,3589 | 0,3572 | 0,3555 | 0,3538 |
| 0,5 | 0,3521 | 0,3503 | 0,3485 | 0,3467 | 0,3448 | 0,3429 | 0,3410 | 0,3391 | 0,3372 | 0,3352 |
| 0,6 | 0,3332 | 0,3312 | 0,3292 | 0,3271 | 0,3251 | 0,3230 | 0,3209 | 0,3187 | 0,3166 | 0,3144 |
| 0,7 | 0,3123 | 0,3101 | 0,3079 | 0,3056 | 0,3034 | 0,3011 | 0,2989 | 0,2966 | 0,2943 | 0,2920 |
| 0,8 | 0,2897 | 0,2874 | 0,2850 | 0,2827 | 0,2803 | 0,2780 | 0,2756 | 0,2732 | 0,2709 | 0,2685 |
| 0,9 | 0,2661 | 0,2637 | 0,2613 | 0,2589 | 0,2565 | 0,2541 | 0,2516 | 0,2492 | 0,2468 | 0,2444 |
| 1,0 | 0,2420 | 0,2396 | 0,2371 | 0,2347 | 0,2323 | 0,2299 | 0,2275 | 0,2251 | 0,2227 | 0,2203 |
| 1,1 | 0,2179 | 0,2155 | 0,2131 | 0,2107 | 0,2083 | 0,2059 | 0,2036 | 0,2012 | 0,1989 | 0,1965 |
| 1,2 | 0,1942 | 0,1919 | 0,1895 | 0,1872 | 0,1849 | 0,1826 | 0,1804 | 0,1781 | 0,1758 | 0,1736 |
| 1,3 | 0,1714 | 0,1691 | 0,1669 | 0,1647 | 0,1626 | 0,1604 | 0,1582 | 0,1561 | 0,1539 | 0,1518 |
| 1,4 | 0,1497 | 0,1476 | 0,1456 | 0,1435 | 0,1415 | 0,1394 | 0,1374 | 0,1354 | 0,1334 | 0,1315 |
| 1,5 | 0,1295 | 0,1276 | 0,1257 | 0,1238 | 0,1219 | 0,1200 | 0,1182 | 0,1163 | 0,1145 | 0,1127 |
| 1,6 | 0,1109 | 0,1092 | 0,1074 | 0,1057 | 0,1040 | 0,1023 | 0,1006 | 0,0989 | 0,0973 | 0,0957 |
| 1,7 | 0,0940 | 0,0925 | 0,0909 | 0,0893 | 0,0878 | 0,0863 | 0,0848 | 0,0833 | 0,0818 | 0,0804 |
| 1,8 | 0,0790 | 0,0775 | 0,0761 | 0,0748 | 0,0734 | 0,0721 | 0,0707 | 0,0694 | 0,0681 | 0,0669 |
| 1,9 | 0,0656 | 0,0644 | 0,0632 | 0,0620 | 0,0608 | 0,0596 | 0,0584 | 0,0573 | 0,0562 | 0,0551 |
| 2,0 | 0,0540 | 0,0529 | 0,0519 | 0,0508 | 0,0498 | 0,0488 | 0,0478 | 0,0468 | 0,0459 | 0,0449 |
| 2,1 | 0,0440 | 0,0431 | 0,0422 | 0,0413 | 0,0404 | 0,0395 | 0,0387 | 0,0379 | 0,0371 | 0,0363 |
| 2,2 | 0,0353 | 0,0347 | 0,0339 | 0,0332 | 0,0325 | 0,0317 | 0,0310 | 0,0303 | 0,0297 | 0,0290 |
| 2,3 | 0,0283 | 0,0277 | 0,0270 | 0,0264 | 0,0258 | 0,0252 | 0,0246 | 0,0241 | 0,0235 | 0,0229 |
| 2,4 | 0,0224 | 0,0219 | 0,0213 | 0,0208 | 0,0203 | 0,0198 | 0,0194 | 0,0189 | 0,0184 | 0,0180 |
| 2,5 | 0,0175 | 0,0171 | 0,0167 | 0,0163 | 0,0158 | 0,0154 | 0,0151 | 0,0147 | 0,0143 | 0,0139 |
| 2,6 | 0,0136 | 0,0132 | 0,0129 | 0,0126 | 0,0122 | 0,0119 | 0,0116 | 0,0113 | 0,0110 | 0,0107 |
| 2,7 | 0,0104 | 0,0101 | 0,0099 | 0,0096 | 0,0093 | 0,0091 | 0,0088 | 0,0086 | 0,0084 | 0,0081 |
| 2,8 | 0,0079 | 0,0077 | 0,0075 | 0,0073 | 0,0071 | 0,0069 | 0,0067 | 0,0065 | 0,0063 | 0,0061 |
| 2,9 | 0,0060 | 0,0058 | 0,0056 | 0,0055 | 0,0053 | 0,0051 | 0,0050 | 0,0048 | 0,0047 | 0,0046 |
| 3,0 | 0,0044 | 0,0043 | 0,0042 | 0,0040 | 0,0039 | 0,0038 | 0,0037 | 0,0036 | 0,0035 | 0,0034 |
| 3,1 | 0,0033 | 0,0032 | 0,0031 | 0,0030 | 0,0029 | 0,0028 | 0,0027 | 0,0026 | 0,0025 | 0,0025 |
| 3,2 | 0,0024 | 0,0023 | 0,0022 | 0,0022 | 0,0021 | 0,0020 | 0,0020 | 0,0019 | 0,0018 | 0,0018 |
| 3,3 | 0,0017 | 0,0017 | 0,0016 | 0,0016 | 0,0015 | 0,0015 | 0,0014 | 0,0014 | 0,0013 | 0,0013 |
| 3,4 | 0,0012 | 0,0012 | 0,0012 | 0,0011 | 0,0011 | 0,0010 | 0,0010 | 0,0010 | 0,0009 | 0,0009 |
| 3,5 | 0,0009 | 0,0008 | 0,0008 | 0,0008 | 0,0008 | 0,0007 | 0,0007 | 0,0007 | 0,0007 | 0,0006 |
| 3,6 | 0,0006 | 0,0006 | 0,0006 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0004 |
| 3,7 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0003 | 0,0003 | 0,0003 | 0,0003 |
| 3,8 | 0,0003 | 0,0003 | 0,0003 | 0,0003 | 0,0003 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 |
| 3,9 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0001 |
Таблица значений интегральной функции Лапласа
| x | Ф(х) | x | Ф(х) | x | Ф(х) | x | Ф(х) | x | Ф(х) | x | Ф(х) |
| 0,00 | 0,0000 | 0,50 | 0,1915 | 1,00 | 0,3413 | 1,50 | 0,4332 | 2,00 | 0,4772 | 3,00 | 0,49865 |
| 0,01 | 0,0040 | 0,51 | 0,1950 | 1,01 | 0,3438 | 1,51 | 0,4345 | 2,02 | 0,4783 | 3,20 | 0,49931 |
| 0,02 | 0,0080 | 0,52 | 0,1985 | 1,02 | 0,3461 | 1,52 | 0,4357 | 2,04 | 0,4793 | 3,40 | 0,49966 |
| 0,03 | 0,0120 | 0,53 | 0,2019 | 1,03 | 0,3485 | 1,53 | 0,4370 | 2,06 | 0,4803 | 3,60 | 0,499841 |
| 0,04 | 0,0160 | 0,54 | 0,2054 | 1,04 | 0,3508 | 1,54 | 0,4382 | 2,08 | 0,4812 | 3,80 | 0,499928 |
| 0,05 | 0,0199 | 0,55 | 0,2088 | 1,05 | 0,3531 | 1,55 | 0,4394 | 2,10 | 0,4821 | 4,00 | 0,499968 |
| 0,06 | 0,0239 | 0,56 | 0,2123 | 1,06 | 0,3554 | 1,56 | 0,4406 | 2,12 | 0,4830 | 4,50 | 0,499997 |
| 0,07 | 0,0279 | 0,57 | 0,2157 | 1,07 | 0,3577 | 1,57 | 0,4418 | 2,14 | 0,4838 | 5,00 | 0,499997 |
| 0,08 | 0,0319 | 0,58 | 0,2190 | 1,08 | 0,3599 | 1,58 | 0,4429 | 2,16 | 0,4846 | ||
| 0,09 | 0,0359 | 0,59 | 0,2224 | 1,09 | 0,3621 | 1,59 | 0,4441 | 2,18 | 0,4854 | ||
| 0,10 | 0,0398 | 0,60 | 0,2257 | 1,10 | 0,3643 | 1,60 | 0,4452 | 2,20 | 0,4861 | ||
| 0,11 | 0,0438 | 0,61 | 0,2291 | 1,11 | 0,3665 | 1,61 | 0,4463 | 2,22 | 0,4868 | ||
| 0,12 | 0,0478 | 0,62 | 0,2324 | 1,12 | 0,3686 | 1,62 | 0,4474 | 2,24 | 0,4875 | ||
| 0,13 | 0,0517 | 0,63 | 0,2357 | 1,13 | 0,3708 | 1,63 | 0,4484 | 2,26 | 0,4881 | ||
| 0,14 | 0,0557 | 0,64 | 0,2389 | 1,14 | 0,3729 | 1,64 | 0,4495 | 2,28 | 0,4887 | ||
| 0,15 | 0,0596 | 0,65 | 0,2422 | 1,15 | 0,3749 | 1,65 | 0,4505 | 2,30 | 0,4893 | ||
| 0,16 | 0,0636 | 0,66 | 0,2454 | 1,16 | 0,3770 | 1,66 | 0,4515 | 2,32 | 0,4898 | ||
| 0,17 | 0,0675 | 0,67 | 0,2486 | 1,17 | 0,3790 | 1,67 | 0,4525 | 2,34 | 0,4904 | ||
| 0,18 | 0,0714 | 0,68 | 0,2517 | 1,18 | 0,3810 | 1,68 | 0,4535 | 2,36 | 0,4909 | ||
| 0,19 | 0,0753 | 0,69 | 0,2549 | 1,19 | 0,3830 | 1,69 | 0,4545 | 2,38 | 0,4913 | ||
| 0,20 | 0,0793 | 0,70 | 0,2580 | 1,20 | 0,3849 | 1,70 | 0,4554 | 2,40 | 0,4918 | ||
| 0,21 | 0,0832 | 0,71 | 0,2611 | 1,21 | 0,3869 | 1,71 | 0,4564 | 2,42 | 0,4922 | ||
| 0,22 | 0,0871 | 0,72 | 0,2642 | 1,22 | 0,3883 | 1,72 | 0,4573 | 2,44 | 0,4927 | ||
| 0,23 | 0,0910 | 0,73 | 0,2673 | 1,23 | 0,3907 | 1,73 | 0,4582 | 2,46 | 0,4931 | ||
| 0,24 | 0,0948 | 0,74 | 0,2703 | 1,24 | 0,3925 | 1,74 | 0,4591 | 2,48 | 0,4934 | ||
| 0,25 | 0,0987 | 0,75 | 0,2734 | 1,25 | 0,3944 | 1,75 | 0,4599 | 2,50 | 0,4938 | ||
| 0,26 | 0,1026 | 0,76 | 0,2764 | 1,26 | 0,3962 | 1,76 | 0,4608 | 2,52 | 0,4941 | ||
| 0,27 | 0,1064 | 0,77 | 0,2794 | 1,27 | 0,3980 | 1,77 | 0,4616 | 2,54 | 0,4945 | ||
| 0,28 | 0,1103 | 0,78 | 0,2823 | 1,28 | 0,3997 | 1,78 | 0,4625 | 2,56 | 0,4948 | ||
| 0,29 | 0,1141 | 0,79 | 0,2852 | 1,29 | 0,4015 | 1,79 | 0,4633 | 2,58 | 0,4951 | ||
| 0,30 | 0,1179 | 0,80 | 0,2881 | 1,30 | 0,4032 | 1,80 | 0,4641 | 2,60 | 0,4953 | ||
| 0,31 | 0,1217 | 0,81 | 0,2910 | 1,31 | 0,4049 | 1,81 | 0,4649 | 2,62 | 0,4956 | ||
| 0,32 | 0,1255 | 0,82 | 0,2939 | 1,32 | 0,4066 | 1,82 | 0,4656 | 2,64 | 0,4959 | ||
| 0,33 | 0,1293 | 0,83 | 0,2967 | 1,33 | 0,4082 | 1,83 | 0,4664 | 2,66 | 0,4961 | ||
| 0,34 | 0,1331 | 0,84 | 0,2995 | 1,34 | 0,4099 | 1,84 | 0,4671 | 2,68 | 0,4963 | ||
| 0,35 | 0,1368 | 0,85 | 0,3023 | 1,35 | 0,4115 | 1,85 | 0,4678 | 2,70 | 0,4965 | ||
| 0,36 | 0,1406 | 0,86 | 0,3051 | 1,36 | 0,4131 | 1,86 | 0,4686 | 2,72 | 0,4967 | ||
| 0,37 | 0,1443 | 0,87 | 0,3078 | 1,37 | 0,4147 | 1,87 | 0,4693 | 2,74 | 0,4969 | ||
| 0,38 | 0,1480 | 0,88 | 0,3106 | 1,38 | 0,4162 | 1,88 | 0,4699 | 2,76 | 0,4971 | ||
| 0,39 | 0,1517 | 0,89 | 0,3133 | 1,39 | 0,4177 | 1,89 | 0,4706 | 2,78 | 0,4973 | ||
| 0,40 | 0,1554 | 0,90 | 0,3159 | 1,40 | 0,4192 | 1,90 | 0,4713 | 2,80 | 0,4974 | ||
| 0,41 | 0,1591 | 0,91 | 0,3186 | 1,41 | 0,4207 | 1,91 | 0,4719 | 2,82 | 0,4976 | ||
| 0,42 | 0,1628 | 0,92 | 0,3212 | 1,42 | 0,4222 | 1,92 | 0,4726 | 2,84 | 0,4977 | ||
| 0,43 | 0,1664 | 0,93 | 0,3238 | 1,43 | 0,4236 | 1,93 | 0,4732 | 2,86 | 0,4979 | ||
| 0,44 | 0,1700 | 0,94 | 0,3264 | 1,44 | 0,4251 | 1,94 | 0,4738 | 2,88 | 0,4980 | ||
| 0,45 | 0,1736 | 0,95 | 0,3289 | 1,45 | 0,4265 | 1,95 | 0,4744 | 2,90 | 0,4981 | ||
| 0,46 | 0,1772 | 0,96 | 0,3315 | 1,46 | 0,4279 | 1,96 | 0,4750 | 2,92 | 0,4982 | ||
| 0,47 | 0,1808 | 0,97 | 0,3340 | 1,47 | 0,4292 | 1,97 | 0,4756 | 2,94 | 0,4984 | ||
| 0,48 | 0,1844 | 0,98 | 0,3365 | 1,48 | 0,4306 | 1,98 | 0,4761 | 2,96 | 0,4985 | ||
| 0,49 | 0,1879 | 0,99 | 0,3389 | 1,49 | 0,4319 | 1,99 | 0,4767 | 2,98 | 0,4986 |
№14 понятие дискретной случайной величины. Закон распределения случайной величины.
Дискретная случайная величина - это величина, которая принимает конкретное значение и этих значений конечное или счетное множество.
Закон распределения случайной величины -это всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
№15 числовые характеристики ДСВ случайной величины.
Математическое ожидание, дисперсия и среднеквадратичное отклонение.
Математическое ожидание -называется сумма произведений всех её значений на соответствие вероятности.
Дисперсия - это математическое ожидание квадрата отклонения случайной величины от её математического ожидания. Дисперсия показывает разброс от среднего значения, чем больше дисперсия, тем больше значение случайной величины отклоняются от среднего.
Среднеквадратичное отклонение нужно для того, что бы убрать квадрат.
№16 функция распределения ДСВ. Плотность вероятности.
ФРДСВ - необходима для того чтобы задать эту величину графически.
ФРДСВ - называется функция F(х), выражающая вероятность того, что случайная величина примет значение меньше, чем конкретное значение х.
Графиком является ступенчатая фигура «скачки» которой соответствуют вероятностям из таблицы.
Случайная величина X называется непрерывной, если ее функция распределения F (х\ непрерывна на всей оси Ох, а плотность распределения f(x) существует везде, за исключением, быть может, конечного числа точек.
Рассмотрим свойства плотности распределения.
Свойство 1. Плотность распределения неотрицательна, т. е. 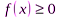
Это свойство непосредственно вытекает из того, что плотность распределения 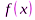 есть производная от неубывающей функции распределения F(x).
есть производная от неубывающей функции распределения F(x).
Свойство 2. Функция распределения случайной величины равна интегралу от плотности в интервале от – ∞ до х, т. е.
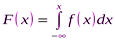 . (3)
. (3)
Свойство 3. Вероятность попадания непрерывной случайной величины X на участок  равна интегралу от плотности распределения, взятому по этому участку, т. е.
равна интегралу от плотности распределения, взятому по этому участку, т. е.
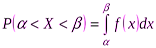 . (4)
. (4)
Свойство 4. Интеграл в бесконечных пределах от плотности распределения равен единице:
 .
.
Если интервал возможных значений случайной величины имеет конечные пределы а и b,то плотность распределения f(х) = 0 вне промежутка  и свойство 4 тогда можно записать так:
и свойство 4 тогда можно записать так:
 .
.
| №17биноминальный и геометрический законы распределения. |
Биномиальный закон распределения.
Для этого закона дискретная случайная величина X – число появлений события А при проведении испытаний, удовлетворяющих схеме Бернулли.
Вероятности ее возможных значений вычисляются по формуле
 .
.
Запишем биномиальный закон в виде таблицы

| ... | 
| ... | 
| ||
| Р | 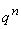
| 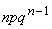
| ... | 
| ... | 
|
M(X)=np; D(X)=npq
Геометрический закон распределения.
Для этого закона дискретная случайная величина X – число проведенных испытаний до первого появления события А, если испытания удовлетворяют схеме Бернулли.
Тогда вероятность того, что в n испытаниях случайная величина X примет значение равное m вычисляется по формуле.
Запишем геометрический закон в виде таблицы
| X | ... | 
| ... | |||
| Р | 
| 
| 
| ... | 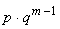
| ... |
№18закон распределения Пуассона
Закон распределения Пуассона.
Для этого закона дискретная случайная величина X – число появлений события А при проведении испытаний, удовлетворяющих теореме Пуассона.
Тогда вероятность того, что в n испытаниях случайная величина X примет значение равное m вычисляется по формуле
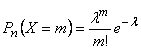 ;
;  , где
, где 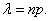
Запишем закон Пуассона в виде таблицы

| ... | 
| ... | ||

| 
| 
| ... | 
| ... |
M(X)=np; D(X)=npq
№19 непрерывная случайная величина. Функция распределения и плотность вероятности НСВ.
НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно.
Можно дать другое, более строгое, определение НСВ, используя понятие функции распределения. Случайная величина Х называется непрерывной, если ее функция распределения F(x) непрерывна на всей числовой оси.
В отличие от дискретных случайных величин вероятность отдельного значения для непрерывной случайной величины равна нулю:  , для любого с из множества действительных чисел. Поэтому для НСВ Х имеем:
, для любого с из множества действительных чисел. Поэтому для НСВ Х имеем:
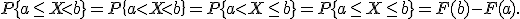
Помимо функции распределения для непрерывных случайных величин, существует еще один удобный способ задания закона распределения - плотность вероятности.
Пусть функция распределения F(x) данной НСВ Х непрерывна и дифференцируема всюду, кроме, может быть, отдельных точек. Тогда производная f(x) ее функции распределения называется плотностью распределения непрерывной СВ Х (или "плотностью вероятности", или просто "плотностью"):
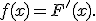
Свойства плотности распределения:
1.  (свойство неотрицательности);
(свойство неотрицательности);
2.  (свойство нормированности);
(свойство нормированности);
3.  ;
;
4.  ;
;
5.  .
.
График плотности распределения f(x) называется кривой распределения.
№20 экспоненциальный закон распределения.
№21 нормальный закон распределения
№22 генеральная совокупность и выборка. Полигон гистограмма. Эмпирическая ф.р.
Генеральная совокупность[1] (в англ. — population) — совокупность всех объектов (единиц), относительно которых учёный намерен делать выводы при изучении конкретной проблемы.
Генеральная совокупность состоит из всех объектов, которые подлежат изучению. Состав генеральной совокупности зависит от целей исследования. Иногда генеральная совокупность - это все население определённого региона (например, когда изучается отношение потенциальных избирателей к кандидату), чаще всего задаётся несколько критериев, определяющих объект исследования. Например, мужчины 30-50 лет, использующие бритву определённой марки не реже раза в неделю, и имеющие доход не ниже $100 на одного члена семьи.
Выборка или выборочная совокупность — множество случаев (испытуемых, объектов, событий, образцов), с помощью определённой процедуры выбранных из генеральной совокупности для участия в исследовании.
Эмпирической функцией распределения (функцией распределения выборки) называют функцию  , определяющую для каждого значения
, определяющую для каждого значения  относительную частоту события
относительную частоту события  , т.е.
, т.е.
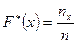 ,
,
где  – число
– число  , меньших
, меньших  ;
; 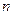 – объем выборки.
– объем выборки.
Из теоремы Бернулли следует, что при достаточно большом объеме выборки функции  и
и  мало отличаются друг от друга. Отличие эмпирической функции распределения от теоретической состоит в том, что теоретическая функция распределения определяет вероятность события
мало отличаются друг от друга. Отличие эмпирической функции распределения от теоретической состоит в том, что теоретическая функция распределения определяет вероятность события  , а эмпирическая функция определяет относительную частоту этого же события.
, а эмпирическая функция определяет относительную частоту этого же события.
Эмпирическая функция распределения обладает всеми свойствами интегральной функции распределения:
1) значения эмпирической функции распределения принадлежат отрезку  ;
;
2)  – неубывающая функция;
– неубывающая функция;
3) если  – наименьшая варианта, то
– наименьшая варианта, то  при
при  ; если
; если  – наибольшая варианта, то
– наибольшая варианта, то  при
при  .
.
№23числовые характеристики выборки.
Показатели положения
Среднее значение выборки вычисляется по формуле
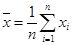 .
.
Выборочной квантилью уровня p называется решение уравнения
 ,
,
где 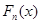 — выборочная функция распределения.
— выборочная функция распределения.
В частности выборочная медиана есть решение уравнения  , т.е. выборочная медиана — это выборочная квантиль уровня 0.5. Выборочная медиана разбивает выборку пополам: слева и справа от нее оказывается одинаковое число элементов выборки. Если число элементов выборки четно,
, т.е. выборочная медиана — это выборочная квантиль уровня 0.5. Выборочная медиана разбивает выборку пополам: слева и справа от нее оказывается одинаковое число элементов выборки. Если число элементов выборки четно,  , то выборочную медиану определяют по формуле
, то выборочную медиану определяют по формуле  , где
, где  и
и 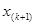 — k -е и (k +1) -е выборочные значения из вариационного ряда. При нечетном n = 2 k + 1объеме выборки за значение медианы принимают величину
— k -е и (k +1) -е выборочные значения из вариационного ряда. При нечетном n = 2 k + 1объеме выборки за значение медианы принимают величину 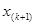 .
.
К показателям положения относятся минимальный и максимальный элементы выборки, а также верхняя и нижняя квартили (они ограничивают зону, в которой сосредоточены 50% элементов выборки).
Показатели разброса
К показателям разброса относятся дисперсия выборки, стандартное отклонение, размах выборки, межквартильный размах, коэффициент эксцесса.
Выборочной дисперсией называется величина
 .
.
Однако в статистике чаще в качестве выборочной дисперсии используется величина
 .
.
Стандартное отклонение вычисляется по формуле  .
.
Размах выборки вычисляется по формуле  .
.
Межквартильный размах равен  , где
, где  — 25%-я квартиль, решение уравнения
— 25%-я квартиль, решение уравнения  ,
,  — 75%-я квартиль, решение уравнения
— 75%-я квартиль, решение уравнения 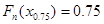 .
.
Выборочный эксцесс вычисляется следующим образом. Сначала отыскивается величина  — выборочный центральный момент 4-го порядка. А затем вычисляется выборочный эксцесс по формуле
— выборочный центральный момент 4-го порядка. А затем вычисляется выборочный эксцесс по формуле  .
.
Показатели асимметрии
Показатели асимметрии дают информацию о симметрии распределения выборочных данных около центра выборки. Сюда в первую очередь относится коэффициент асимметрии, который вычисляется по формуле
 ,
,
где  — выборочный центральный момент 3-го порядка, а
— выборочный центральный момент 3-го порядка, а  —стандартное отклонение, формула для которого приведена выше.
—стандартное отклонение, формула для которого приведена выше.
№24понятие множества. Способы заданий. Подмножества.
Множества-совокупность объектов любой природы.
Перечисление, указание характеристического свойства. Бывают конечные, бесконечные. Пустые, непустые.
Подмножество- элементы, входящае в множество.
№25 операции над множествами. Диаграммы Эйлера-Венна.
Объединение.
Пересечение.
Разность.
Симметрическая разность.
Дополнение.
№26 законы теории множеств.
Коммутативность.
№27 формула включений и исключений.
№28 понятие высказывания. Операции над высказываниями. Таблицы истинности.
Понятие высказывания. Основным понятием математической логики является понятие «простого высказывания». Под высказыванием понимается предложение, представляющее собой такое утверждение, о котором можно судить, истинно оно или ложно. Логическими значениями высказываний являются «истина» и «ложь».
Приведем примеры высказываний.
- Москва – столица России.
- Омск находится на берегу Волги.
- 3+2=5.
- Кислород – газ.
- 3<2.
Высказывания 1), 3), 4) истинны, а высказывания 2), 5) ложны.
Не всякое предложение является высказыванием. К высказываниям не относятся вопросительные и восклицательные предложения. Предложения «Математика – интересный предмет», «Осень – лучшая пора года» не являются высказываниями, так как нет единого мнения о том, истинны эти предложения или ложны. Предложения «Сегодня плохая погода», «3 х <2» также не являются высказываниями, для того чтобы определить их истинность или ложность, нужны дополнительные сведения: конкретный день, о котором идет речь; значение, которое принимает х.
Высказывания, представляющие собой одно утверждение, называют простым или элементарным. Из элементарных высказываний с помощью логических связок можно построить высказывания, называемые сложными или составными. Образование составного высказывания с помощью логической связки называют
Поделиться:
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2016-08-20
Нарушение авторских прав и Нарушение персональных данных