Анализ чувствительности показателей широко используется в практике инвестиционного менеджмента. В общем случае он сводится к исследованию зависимости некоторого результативного показателя от вариации значений показателей, участвующих в его определении. Другими словами, этот метод позволяет получить ответы на вопросы вида: что будет с результативной величиной, если изменится значение некоторой исходной величины? Отсюда его второе название - анализ "что будет, если".
Как правило, проведение подобного анализа предполагает выполнение следующих шагов:
1. Задается взаимосвязь между исходными и результирующим показателями в виде математического уравнения или неравенства.
2. Определяются наиболее вероятные значения для исходных показателей и возможные диапазоны их изменения.
3. Путем изменения значений исходных показателей исследуется их влияние на конечный результат.
Проект с меньшей чувствительностью критерия эффективности (NPV, IRR) считается менее рискованным.
Обычная процедура анализа чувствительности предполагает изменение одного исходного показателя, в то время как значения остальных считаются постоянными величинами.
Пример 3. Фирма рассматривает инвестиционный проект, связанный с выпуском продукта А. Полученные в результате опроса экспертов данные о проекте приведены в табл.7. Необходимо провести анализ чувствительности NPV к изменениям ключевых исходных показателей.
Первым этапом анализа согласно сформулированному выше алгоритму является определение зависимости результирующего показателя от исходных.
В данном случае с учетом приведенных в табл.7 обозначений подобная зависимость может быть задана следующим соотношением:
|
|
Диапазоны возможного изменения исходных показателей были определены ранее (см. табл.7), поэтому можно приступать к анализу.
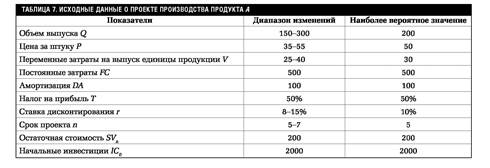
Выберем параметр, влияние которого будет исследоваться. Предположим, что таким параметром является цена. Диапазон ее изменений составляет 35-55. Вычислим критерий NPV по формуле (14), варьируя значения цены (например, от 50 до 30 с шагом, равным 5), при этом остальные параметры неизменны.
Результаты проведенных расчетов представлены ниже.
Из результатов анализа следует, что при условии постоянства значений остальных показателей падение цены менее чем на 30% приведет к отрицательной величине чистой приведенной стоимости проекта. Тогда как, например, снижение объемов выпуска Q более чем на 30% при прочих равных условиях все еще обеспечивает положительную величину NPV ( проверьте это самостоятельно).
Анализ чувствительности проекта к другим параметрам проводится аналогичным способом.
Метод анализа чувствительности является хорошей иллюстрацией влияния отдельных исходных показателей на результат. А также можно определить направления дальнейших исследований: если установлена сильная чувствительность результирующего показателя к изменениям конкретного исходного показателя, последнему следует уделить особое внимание.
Вместе с тем данный метод обладает и рядом недостатков, наиболее существенными из которых являются:
жесткая детерминированность моделей, используемых для связи ключевых переменных;
данный метод не позволяет получить вероятностные оценки возможных отклонений исходных и результирующих показателей;
|
|
данный метод предполагает изменение одного исходного показателя, в то время как остальные считаются постоянными величинами, однако в действительности показатели взаимосвязаны, и изменение одного из них автоматически приводит к изменению остальных.
Следует отметить, что применение современных компьютеров и специальных пакетов прикладных программ позволяет преодолеть последний из перечисленных недостатков. В частности, в MS Excel можно проводить подобный анализ одновременно по двум параметрам, а в пакетах прикладных программ Project Expert - более чем по двум.
Метод сценариев
Метод сценариев (в отличие от методов, рассмотренных ранее) позволяет совместить исследование чувствительности результирующего показателя с анализом вероятностных оценок его отклонений. В общем случае процедура использования данного метода в процессе анализа инвестиционных рисков включает выполнение следующих шагов.
Определяют несколько вариантов изменения ключевых исходных показателей (например, пессимистический, наиболее вероятный и оптимистический).
Каждому варианту изменения приписывают его вероятностную оценку.
Для каждого варианта рассчитывают вероятное значение выбранного критерия, а также оценки его отклонения от среднего значения.
Проводится анализ вероятностных распределений полученных результатов.
При прочих равных условиях проект с наименьшим стандартным отклонением о считается менее рискованным.
Пример 4. Предположим, что по результатам анализа проекта (пример 3) был составлен ряд сценариев его развития и были определены вероятности их осуществления (табл.8). Необходимо провести анализ собственного риска проекта при условии, что все остальные параметры считаются постоянными (см. табл.7).
|
|
Прежде всего необходимо определить значение NPV для каждого сценария, например, с помощью соотношения (14). С целью сокращения необходимых вычислений эти значения представлены в табл.8.
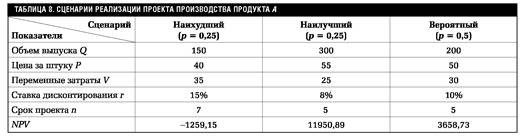
Полученные данные свидетельствуют о том, что разброс возможных результатов достаточно велик.
Определим среднее ожидаемое значение чистой приведенной стоимости NPV - величину Е (NPV):
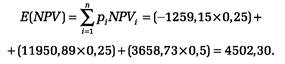
Для того чтобы вычислить стандартное отклонение, можно воспользоваться следующим соотношением:
Зная основные характеристики распределения NPV, мы можем приступать к проведению вероятностного анализа. Для удобства будем полагать, что величина NPV имеет нормальное распределение вероятностей. Этот закон распределения широко используется на практике. Кроме того, он полностью описывается двумя рассмотренными выше параметрами 
и обладает рядом замечательных свойств, существенно упрощающих проведение анализа. В частности, следствием одного из таких свойств, известного как правило "трех сигм", является утверждение, что вероятность попадания нормально распределенной случайной величины в интервал 
приблизительно равна около 68% (рис.3).
Таким образом, с вероятностью 68% можно утверждать, что NPV проекта будет находиться в интервале 4502,30 ± 4746,02 (от -243,72 до 9248,32). Следовательно, вероятность отклонения от ожидаемого значения в меньшую или большую сторону на величину 
будет равна примерно 34%.
Теоретически, зная параметры нормального распределения Е и у, мы можем определить вероятность того, что случайная величина NPV будет меньше (больше) любого заданного значения Х из следующего соотношения:
где Ф - функция Лапласа. Значения функции Лапласа приводятся в специальных справочных статистических таблицах. Для выполнения подобных расчетов можно также использовать стандартные офисные программы типа MS Excel. Ниже приведен фрагмент электронной таблицы MS Excel с результатами вероятностного анализа для рассматриваемого примера (рис.4).
Полученные результаты в целом свидетельствуют о наличии определенного риска применительно к этому проекту. Несмотря на то, что среднее значение NPV ( 4502,30) превышает прогноз экспертов (3658,73), величина этого показателя меньше стандартного отклонения. Вероятность получения нулевого результата равна 17%, таким образом, существует один "шанс" из шести, что вы понесете убытки.
В целом метод сценариев позволяет получить достаточно наглядную картину результатов для различных вариантов реализации проектов. Он обеспечивает менеджера информацией как о чувствительности выбранного критерия эффективности, так и о возможных отклонениях последнего.
Применение программных средств типа MS Excel позволяет значительно повысить эффективность и наглядность подобного анализа путем практически неограниченного увеличения числа сценариев, введения дополнительных (до 32) ключевых переменных, построения графиков распределения вероятностей и т.д. Вместе с тем использование данного метода направлено на исследование поведения только результативных показателей, таких как NPV или IRR. Метод сценариев не обеспечивает пользователя информацией о возможных отклонениях потоков платежей и других ключевых показателей, определяющих в конечном итоге ход реализации проекта. Несмотря на ряд присущих ему ограничений, данный метод успешно применяется во многих разделах инвестиционного и финансового анализа.
Деревья решений
Деревья решений обычно используются для анализа рисков проектов, имеющих обозримое или разумное число вариантов развития. Они особо полезны в ситуациях, когда решения, принимаемые в момент времени t, сильно зависят от решений, принятых ранее, и в свою очередь определяют сценарии дальнейшего развития событий.
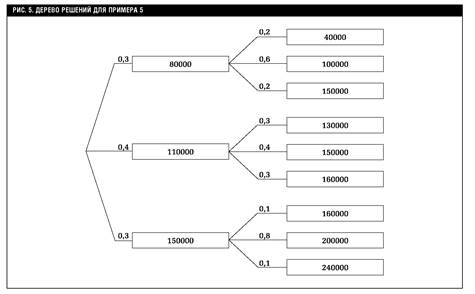
Дерево решений имеет вид графа. Его вершины представляют ключевые состояния, в которых возникает необходимость выбора, а дуги (ветви дерева) - различные события (решения, последствия, операции), которые могут произойти в ситуации, определяемой вершиной. Каждой дуге могут быть приписаны числовые характеристики (нагрузки), например величина платежа и вероятность его осуществления. Графический вид дерева решений для рассматриваемого ниже примера приведен на рис.5.
В общем случае использование данного метода предполагает выполнение следующих шагов.
Для каждого момента времени t определяют проблему и все возможные варианты дальнейшего развития событий.
Отмечают на дереве соответствующую конкретной проблеме вершину и исходящие из нее дуги.
Каждой исходящей дуге приписывают ее стоимостную и вероятностную оценку.
Исходя из значений всех вершин и дуг рассчитывают вероятное значение критерия NPV ( либо IRR, PI).
Анализируют вероятностные распределения полученных результатов.
Пример 5. Рассматривается двухлетний проект, требующий первоначальных вложений в объеме 200 тыс. руб. Согласно экспертным оценкам, приток средств от реализации проекта в первом году с вероятностью 0,3 составит 80 тыс. руб., с вероятностью 0,4 - 100 тыс. руб. и с вероятностью 0,3 - 150 тыс. руб. Показатели притока средств во второй период зависят от результатов, полученных за первый период (табл.9).
Ставка дисконтирования равна 12%. Необходимо построить дерево решений с целью оценки рисков проекта.
Значения NPVi были рассчитаны исходя из дисконтных множителей, равных 0,893 для первого и 0,797 для второго периода соответственно, т.е.:
Значения рi здесь представляют собой совместные вероятности двух событий, т.е. вероятность того, что произойдет и событие 1, и событие 2:
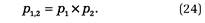
Суммарная ожидаемая NPV рассчитана как сумма произведений NPVi на совместные вероятности рi:
Поскольку суммарная ожидаемая NPV положительна (19024,40), при отсутствии других альтернатив проект можно принять. В общем случае предпочтение следует отдавать проектам с большей ожидаемой NPV ( табл.10).
Следует отметить, что с ростом числа периодов реализации проекта (даже при неизменном количестве альтернатив) структура дерева сильно усложнится.
Например, для трехлетнего проекта число анализируемых путей будет равно уже 27. Весьма полезным и уместным здесь может оказаться шуточный совет: "Деревья решений подобны виноградной лозе: продуктивны только в том случае, если их тщательно и регулярно подрезать".
Быстрый рост сложности вычислений, а также необходимость применения специальных программных средств для реализации подобных моделей - это основные причины невысокой популярности данного метода оценки рисков.
Преодолеть многие ограничения, присущие всем рассмотренным методам, позволяет имитационное моделирование - одно из наиболее мощных средств анализа экономических систем. Вместе с тем его использование требует применения современных компьютеров и соответствующих программных средств.