Курсовой проект по дисциплине 2 глава

· δ ≈ (0,25 + D)10^-3 − при 2 р ≥ 4.

Для двигателей средней и большой мощности:

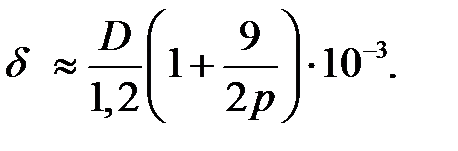
1.4.4. Расчёт ротора

Рис. 2 – Паз ротора

Внешний диаметр магнитопровода ротора D₂:

D ₂ = D – 2 δ.

Внутренний диаметр магнитопровода ротора:

D_j= D _в =k _в D_а,

где коэффициент k _в определяется по табл. П10А.

При проектировании зубцовой зоны короткозамкнутых роторов особое вни­мание следует уделять выбору числа па­зов ротора. Это объясняется тем, что в поле воздушного зазора машины кроме основной присутствует целый спектр гар­моник более высокого порядка, каждая из которых наводит ЭДС в обмотке ротора, поэтому ток в стержнях обмотки имеет сложный гармонический состав. В результате взаимодействия токов и полей высших гармоник возникают электромагнитные моменты, которые при неблагоприятном соотношении Z ₁ и Z ₂ могут существенно ухудшить механическую характеристику двигателя.

Исследования, проведенные для изучения влияния соотношений чисел зубцов на статоре и роторе на характеристику момента, а также на шумы и вибрации, позволили определить наилучшие сочетания Z ₁ и Z ₂ (табл. П9А).

Зубцовое деление t ₂, представляющее собой расстояние между центрами соседних пазов по окружности ротора, рассчитывается по формуле:

t ₂ =π D ₂ /Z ₂.

В асинхронных двигателях с короткозамкнутым ротором серии АИР с высотой оси вращения h ≤ 250 мм выполняют грушевидные пазы и литую обмотку на роторе (рис. 2). В двигателях с h < 160 мм пазы имеют узкую прорезь со следующими размерами [1]:

− b _ш2 = 1 мм, h _ш2 = 0,5 мми h' _ш2 = 0 − при h < 100 мм;

− b _ш2 = 1,5 мм, h _ш2 = 0,75 мми h' _ш2 = 0 − при h =112 и 132 мм;

В двигателях с h = 160…250 мм:

− b _ш2 = 1,5 мм, h _ш2 = 0,7 мми h '_ш2 = 0,3 − при 2 p ≥ 4;

− b _ш2 = 1,5 мм, h _ш2 = 0,7 мми h' _ш2 = 1…1,5 − при 2 p = 2.

Размеры паза b ₁, b ₂ и h ₁ (рис. 2), рассчитывают, исходя из сечения стержня q_c и из условия постоянства ширины зубцов ротора.

Индукция в зубце ротора принимается B_{z 2} = 1,75…1,95 Тл (расчет рекомендуется начинать со среднего значения), тогда ширина зубца определится по следующей формуле:

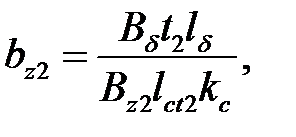
где l _ст2 = l_δ − при длине воздушного зазора меньше 0,3 м.

Далее необходимо определить ток в стержне ротора:

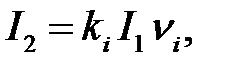
где значение коэффициента k_i определяются по рис. П6Б;

ν_i − коэффициент приведения статорного тока к току в стержне беличьей клетки:

 

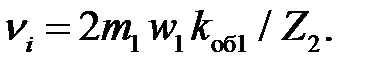
Сечение стержня определяется током I ₂и плотностью тока в стержне J ₂:

q_c = I ₂ / J ₂,

где J ₂= 2,5…3,5 А/мм² − допустимая плотность тока в стержнях для асинхронных двигателей со степенью защиты IP44 и алюминиевой беличьей клеткой. Верхние пределы J ₂ относятся к двигателям меньшей мощности P ₂ = 3…5,5 кВт.

Площадь паза ротора условно можно представить в виде следующих геометрических фигур:

− верхней полуокружности с диаметром b _1р,

− нижней полуокружности с диаметром b _2р ,

− трапеции с основаниями b _1р, b _2р и высотой h _1р .

Широкая часть паза b _1ропределяется по формуле:

Узкая часть паза b _2р [1]:

По условиям высококачественной заливки пазов алюминием b _2р ≥ 1,5 мм (при h ≥ 160 мм –не менее2,5 мм).

Расстояние между центрами полуокружностей или высота трапеции:

Полная высота паза ротора (рис. 2):

Сечение стержня q_c:

Рис. 3 – Размеры короткозамыкающих колец

 

Ток в короткозамыкающих кольцах находят [1]:

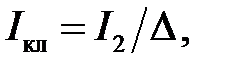
где

При расчете в градусах π = 180 ^°,а в радианах π = 3,14.

Площадь поперечного сечения замыкающих колец:

q _кл = I _кл / J _кл,

где J _кл =0,85 J ₂.

Уменьшение плотности тока в кольцах на 15% ведет к усилению оттока тепла из стержней к кольцам.

Высоту сечения кольца выбирают h _кл ≥ 1,2 h _п2.

Ширину замыкающих колец рассчитывают исходя из q _кл, и выбранной h _кл:

b _кл = q _кл / h _кл.

Средний диаметр замыкающих колец:

D _кл.ср = D ₂ – h _кл.

 

1.4.5. Расчёт намагничивающего тока

Расчет магнитной цепи проводят для режима холостого хода, при котором для асинхронных двигателей характерно относительно сильное насыщение стали зубцов статора и ротора. Магнитная цепь состоит из следующих участков:

− воздушный зазор,

− зубцы статора,

− зубцы ротора,

− ярмо статора,

− ярмо ротора.

Для проведения потока через эти разнородные участки потребуются различные магнитодвижущие силы, сумма которых и определит намагничивающий ток в статорной обмотке.

1. Магнитное напряжение воздушного зазора, А,

где B_δ – индукция в воздушном зазоре, Тл;

δ – воздушный зазор, м;

k_δ – коэффициент воздушного зазора, учитывающий увеличение магнитного сопротивления шлицевыми зонами пазов статора (шлицевыми зонами пазов ротора пренебрегаем, так как они в несколько раз меньше);

μ ₀ — магнитная проницае­мость: μ ₀ = 4π · 10^-7 Гн/м.

Подставив значение μ ₀получим:

Коэффициент воздушного зазора определяется по следующим формулам [1]:

;

2. Магнитное напряжение зубцовой зоны статора:

где h_{z 1} – расчетная высота зубца статора, м;

H_{z 1} – расчетная напряженность поля в зубце, А.

Расчетную высоту зубцов h_{z 1} принимают равной высоте паза статора:

h_{z 1} = h _п1.

Индукция в зубце, Тл,

.

Расчетную напряженность поля H_{z 1} при индукции В_{z 1} определяют по табл. П11А.

3. Магнитное напряжение зубцовой зоны ротора:

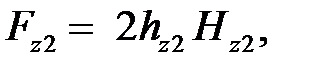
где h_{z 2} – расчетная высота зубца ротора, м;

H_{z 2} – расчетная напряженность поля в зубце, А.

Расчетную высоту зубцов h _z2 определяют по формуле [1]:

h _z2 = h _п2 – 0,1 b _2р.

Индукция в зубце, Тл,

.

Расчетную напряженность поля H_z2 при индукции В_z2 определяют по табл. П11А.

Коэффициент насыщения зубцовой зоны [1]:

Если k_z > 1,5, то имеет место чрезмерное насыщение зубцовой зоны; если k_z < 1,2 — машина не насыщена.

4. Магнитное напряжение ярма статора, А

F_a = L_a H_a,

где L_a – длина средней магнитной силовой линии в ярме статора, м,

L_a =π (D_a – h_a) / (2 p).

Индукция в ярме статора, Тл,

В_а = Ф / (2 h_а l _ст1 k _c).

Н_а – напряженность поля при индукции В_а определяют по табл. П12А, А/м.

5. Магнитное напряжение ярма ротора, А,

F_j = L_j H_j,

где L_j – длина средней магнитной линии потока в ярме ротора, м,

L_j = 2 h'_j – при 2 p = 2;

L_j = π (D _в – h'_j) / (2 p) – при 2 p > 2;

где h'_j – расчетная высота ярма ротора [1], м,

— при 2 p ≤ 4. В этой формуле учитывается то, что часть магнитных силовых линий потока замыкается через вал;

— при 2 p ≥ 6.

Индукция в ярме ротора, Тл,

В_j = Ф / (2 h'_j l _ст2 k _c),

где H_j – напряженность поля в ярме при индукции B_j определяют по табл. П12А, А/м.

Суммарное магнитное напряжение магнитной цепи (на пару полюсов), А,

F_u = F_δ + F_z1 + F_z2 + F_a + F_j.

Коэффициент насыщения магнитной цепи

k_μ = F_u / F_δ.

Намагничивающий ток, А,

Намагничивающий ток выражается также в процентах или в до­лях номинального тока двигателя:

.

Намагничивающий ток . В небольших двигателях мощностью менее 2…3 кВт может достигать 0,5…0,6.

 

1.4.6. Расчёт параметров рабочего режима

1. Активное сопротивление фазы обмотки статора, Ом,

где L – общая длина эффективных проводников фазы обмотки, м;

q _эф – площадь поперечного сечения эффективного проводника, м²;

а – число параллельных ветвей обмотки;

ρ ₁₁₅ – удельное сопротивление материала обмотки при расчетной температуре, Ом·м. Для класса нагревостойкости изоляции F допустимая температура составляет 155℃. Стандартная температура окружающей среды составляет 40℃, следовательно, расчетная температура равна ϑ _расч =155 – 40 = 115℃. Для меди ρ ₁₁₅ =10^-6/41 Ом·м.

Общая длина проводников фазы обмотки L, м,

L = l _cp w ₁,

где l _cp — средняя длина витка обмотки, м;

w ₁ — число витков фазы. Среднюю длину витка l _ср находят как сумму прямолинейных па­зовых и изогнутых лобовых частей катушки:

l _ср = 2 (l _п + l _л).

Длина пазовой части l _п равна конструктивной длине сердечни­ков машины:

l _п = l ₁₍₂₎= l_δ..

Длина лобовой части, м

l _л = K _л b _кт + 2 В;

Вылет лобовых частей обмотки, м

l _выл = K _л b _кт + В.

В этих формулах b _кт – средняя ширина катушки, м, определяемая по окружности, проходящей по серединам высоты пазов:

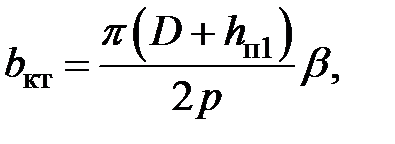
где β – укорочение шага обмотки статора. Для однослойных обмоток β =1;

Для двухслойных обмоток:

– β = 0,79…0,83 – при 2 p ≥ 4. В этом случае достигается значительное уменьшение амплитуды 5 и 7 гармоник [1];

– β = 0,58…0,63 – при 2 p = 2. В этом случае достигается уменьшение длины лобовой части практически в два раза, что ведет к уменьшению активного сопротивления и к уменьшению электрических потерь в статорной обмотке. Кроме того это приведет к уменьшению индуктивного сопротивления, как это будет показано дальше, и к увеличению максимального момента. С другой стороны, это уменьшит площадь охлаждения и, как следствие, приведет к ухудшению охлаждения обмотки.

К _л и К _выл – коэффи­циенты, значения которых приведены в табл. П13А в зависимости от числа полюсов машины и наличия изоляции в лобовых частях;

В = 0,01 м – длина вылета прямолинейной части катушек из паза от торца сердечника до начала отгиба лобовой части.

Длина вылета лобовой части обмотки, м

l _выл = К _выл b _кт + В.

Относительное значение активного сопротивления обмотки статора:

r _1∗ = r ₁ I _1н / U _1н .

Допустимые значения r _1∗ = 0,03…0,05.

2. Активное сопротивление фазы короткозамкнутого ротора.

За фазу обмотки, выполненной в виде беличьей клетки, принимают один стержень и два участка замыкающих колец. Токи в стержнях и за­мыкающих кольцах различны, поэтому их сопротивления при рас­чете общего сопротивления фазы должны быть приведены к одному току. Таким образом, сопротивление фазы короткозамкнутого ро­тора r ₂ является расчетным параметром, полученным из условия равенства электрических потерь в сопротивлении r ₂ от тока I ₂ и сум­марных потерь в стержне и участках замыкающих колец соответственно от тока в стержне I _c и тока в замыкающем кольце I _кл реальной машины:

,

где I _с – ток в стержне ротора;

I _кл – ток в замыкающих кольцах;

r _с – сопротивление стержня;

r _кл – сопротивление участка замыка­ющего кольца, заключенного между двумя соседними стержнями.

Ток I _с называют током ротора и в расчетах обозначают I ₂.

Учитывая, что

I _кл = I _с / Δ = I ₂ / Δ,

где ,

тогда

,

где ;

.

В этих выражениях l _с– полная длина стержня, равная расстоя­нию между замыкающими кольцами, м; D _кл.ср – средний диаметр замыкающих колец, м;

ρ _с115 = ρ _кл115 = 10^-6/20,5 Ом·м – соответственно удельные сопротивления материала (алюминий) стержня и замыкающих колец, при расчетной температуре 115℃.

Сопротивление r ₂ для дальнейших расчетов должно быть приве­дено к числу витков первичной обмотки. Выражение коэффициента приведения для сопротивления фазы короткозамкнутого ротора по­лучают:

.

Приведенное значение активного сопротивления фазы обмотки короткозамкнутого ротора

r' ₂ = r ₂ v ₁₂.

Относительное значение

r' _2∗ = r' ₂ I _1н /U _1н.

Допустимые значения r' _2∗ = 0,015…0,03

3. Индуктивное сопротивление рассеяния обмотки статора асинх­ронного двигателя с короткозамкнутым ротором рассчитывается по формуле [1]:

.

• Коэффициент магнитной проводимости пазового рассеяния (обозначения в формуле соответствуют рис. 1):

,

где b _из – пазовая изоляция,

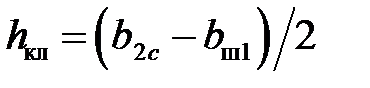– при угле скоса 45°, при – 30° необходимо h _клразделить на .

– при однослойной обмотке (P ₂ < 15 кВт, β =1);

и – при двухслойной обмотке [1].

• Коэффициент магнитной проводимости лобового рассеяния:

,

где q – число пазов на полюс и фазу;

l _л1 – длина лобовой части;

τ – полюсное деление.

• Коэффициент магнитной проводимости дифференциального рассеяния:

,

где k_𝛿 – коэффициент воздушного зазора;

ξ ₁ – коэффициент учета скоса пазов [1]:

,

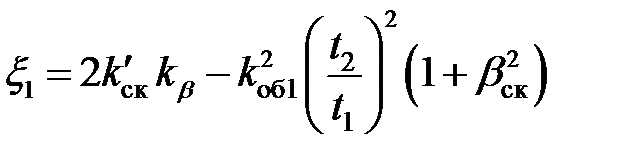где ;

– коэффициент, который определяют по рис. П14Б.

Сумма коэффициентов магнитных проводимостей статорной обмотки:

Σ λ ₁= λ _п1+ λ _л1 + λ _д1.

Относительное значение индуктивного сопротивления статорной обмотки:

x _1∗ = x ₁ I _1н / U _1н, которое находится в пределах x _1∗ = 0,08…0,12.

4. Индуктивное сопротивление обмотки короткозамкнутого ротора [1]:

,

• Коэффициент магнитной проводимости пазового рассеяния (обозначения в формуле соответствуют рисунку 2):

λ _п2 = [ k 1]∙ k_Д + [ k 2] + [ k 3]/ k_I,

где — коэффициент проводимости в верхней полуокружности (b _1р – широкая часть паза), в трапецеидальной части (h _1p) и в нижней полуокружности (b _2р);

— коэффициент проводимости в шлицевой части;

— коэффициент проводимости в перемычке.

В рабочих режимах k_Д = k_I =1.

• Коэффициент магнитной проводимости лобового рассеяния:

.

В этих формулах: D _кл.ср – средний диаметр замыкающих колец;

Δ = 2 sin(π p / Z ₂) – коэффициент приведения токов в кольце к току в стержне;

h _кл и b _кл – средние высота и ширина колец.

• Коэффициент магнитной проводимости дифференциального рассеяния обмотки:

,

где ξ ₂ = 1 – для роторов с литой беличьей клеткой.

Сумма коэффициентов магнитных проводимостей роторной обмотки:

Σ λ ₂= λ _п2+ λ _л2 + λ _д2.

Приведенное значение индуктивного сопротивления фазы обмотки короткозамкнутого ротора:

x' ₂ = x ₂ v ₁₂.

Относительное значение индуктивного сопротивления роторной обмотки:

x' _2∗ = x' ₂ I _1н / U _1н, которое находится в пределах x' _2∗ = 0,08…0,15.

 

1.4.7. Расчёт потерь

Потери в асинхронных машинах подразделяют на потери в стали (основные и добавочные), электрические, вентиляционные, меха­нические и добавочные при нагрузке.

Основные потери в стали в асинхронных двигателях рассчитыва­ют только в сердечнике статора, так как частота перемагничивания ротора, равная f ₂ = s · f ₁, в режимах, близких к номинальному, очень мала и потери в стали ротора даже при больших индукциях незна­чительны.

В пусковых режимах f ₂ близка к f ₁ и потери в стали ротора соответственно возрастают, однако при расчете пусковых характеристик потери находят только для определения нагрева ротора за время пуска. Наибольшими потерями в пусковых режимах являются элект­рические потери в обмотках. Они во много раз превышают потери номинального режима, поэтому пренебрежение потерями в стали ротора при больших скольжениях не вносит сколько-нибудь замет­ной погрешности в расчет.

Основные потери в стали статоров асинхронных машин определяют по следующей формуле:

где p _1,0/50 – удельные потери при индукции 1 Тл и частоте перемагничивания 50 Гц по табл. П14А. Для стали 2013 p _1,0/50 = 2,5…2,6 Вт/кг.

k _{д а} и k _дz – коэффициенты, учитывающие влияние на потери в стали неравномерности распределения потока по сечениям участков магнитопровода и технологических факторов. Для машин мощностью меньше 250 кВт приближенно можно принять k _{д а} = l,6 и k _{д z} = 1,8; для машин большей мощности k _{д а} = 1,4 и k _{д z} = 1,7;

В_а и В _z1 — индукции в ярме и в зубцах статора, Тл;

m_а, m_{z 1} – масса стали ярма и зубцов статора, кг:

m_a = π (D_a – h_a) h_a l _ст1 k _c1 γ _c;

m_{z 1} = h_{z 1} b _z1 Z ₁ l _ст1 k _c γ _c;

где h_а – высота ярма статора;

h_{z 1} = h _п1 – расчетная высота зубца статора;

b _z1 – ширина зуб­ца статора;

l _ст1= l _δ – длина стали статора;

γ _с – удельная масса стали, в расчетах принимают γ _с = 7,8 · 10³ кг/м³.

Добавочные потери в стали (добавочные потери холостого хода) подразделяют на поверхностные (потери в поверхностном слое ко­ронок зубцов статора и ротора от пульсаций индукции в воздушном зазоре) и пульсационные потери в стали зубцов (от пульсации ин­дукции в зубцах).

Для определения поверхностных потерь вначале находят ампли­туду пульсации индукции в воздушном зазоре над коронками зуб­цов статора и ротора, Тл:

B ₀₁₍₂₎ = β ₀₁₍₂₎ k_δ B_δ.

Для зубцов статора β ₀₁ зависит от отношения ширины шлица пазов ротора к воздушному зазору: β ₀₁ = f (b _ш2 / δ); для зубцов ротора – от отношения ширины шлица пазов статора к воздушно­му зазору: β ₀₂ = f (b _ш1 / δ).

По В ₀ и частоте пульсаций индукции над зубцами, равной Z ₂ n для статора и Z ₁ n для ротора, рассчитывают удельные поверхност­ные потери, т.е. потери, приходящиеся на 1м² поверхности головок статора и ротора:

для статора:

;

для ротора:

В этих выражениях k ₀₁₍₀₂₎ – коэффициент, учитывающий влияние обработки поверхности головок зубцов статора (ротора) на удель­ные потери; если поверхность не обрабатывается (двигатели мощ­ностью до 160 кВт, сердечники статоров которых шихтуют на цилиндрические оправки), то k ₀₁₍₀₂₎ = 1,4...1,8, при шлифованных поверхностях (наружная поверхность роторов машин средней и большой мощности и внутренняя поверхность статора двигателей Р ₂ > 160 кВт) k ₀₁₍₀₂₎ = 1,7...2,0; n = n ₁ (1 – s) ≈ n ₁ – частота вращения двигателя, об/мин.

Полные поверхностные потери статора, Вт:

Р _пов.1 = p _пов.1(t_{z 1} – b _ш1) Z ₁ l _ст1.

Полные поверхностные потери ротора, Вт:

Р _пов2 = p _пов2 (t_{z 2} – b _ш2) Z ₂ l _cт2.

Для определения пульсационных потерь вначале находится амплитуда пульсаций индукции в среднем сечении зубцов В _пул, Тл: