Курсовой проект по дисциплине 3 глава

- для зубцов статора:

;

- для зубцов ротора:

.

В этих формулах B_{z 1} и B_{z 2} – индукции в зубцах ста­тора и ротора:

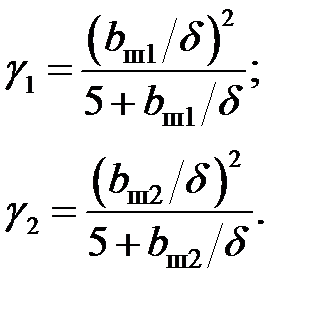
Пульсационные потери в зубцах статора [1]:

пульсационные потери в зубцах ротора:

где m_{z 2} – масса стали зубцов ротора, кг:

m_{z 2} = Z ₂ h_{z 2} b_{z 2} l _ст2 k _c2 γ _c,

где h_{z 2} = h _п2 – 0,1 b _2р — расчетная высота зубца ротора, м;

b_{z 2} – ширина зубца ротора, м:

В общем случае добавочные потери в стали

Р _стдоб = Р _пов1 + Р _пул1 + Р _пов2 + Р _пул2.

и полные потери в стали асинхронных двигателей

P _ст = Р _ст.осн + Р _ст.доб.

Обычно Р _ст.доб приблизительно в 5-8 раз меньше, чем Р _ст.осн..

Электрические потери в асинхронных двигателях рассчитывают раздельно в обмотках статора и ротора.

Электрические потери во всех фазах обмотки статора, Вт,

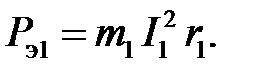
Электрические потери в обмотке короткозамкнутого ротора, Вт,

.

Потери на трение в подшипниках и вентиляционные потери в двигателях с радиальной системой вентиляции без радиальных вен­тиляционных каналов, с короткозамкнутым ротором и вентиляци­онными лопатками на замыкающих кольцах, Вт [1],

Р _мех ≈ К _т(n / 1000)²(10· D)³.

В двигателях с радиальной системой вентиляции средней и боль­шой мощности

Р _мех = 1,2·2 р · τ ³(n _к + 1,1) · 10³,

где n _к – число радиальных вентиляционных каналов; при отсутствии радиальных каналов n _к = 0.

В двигателях с аксиальной системой вентиляции

Р _мех = К _т (n / 1000)² · (10 D _вент)³,

где D _вент – наружный диаметр вентилятора, м; в большинстве кон­струкций можно принять D _вент ≈ D_a; K _т = 2,9 для двигателей с D_a ≤ 0,25 м; К _т = 3,6 для двигателей с D_a = 0,25...0,5 м.

В двигателях большой мощности (0,5 < D_a < 0,9 м)

Р _мех = К _т(10 D_a)³.

При расчетах потерь и КПД двигателей в режимах, отличных от номинального, значение добавочных потерь пересчитывают пропорционально квадрату токов:

Р _доб = Р _{доб.ном}(I ₁ / I _1ном)².

Коэффициент полезного действия двигателя

η = Р ₂ /P ₁ = 1 – Σ P / P ₁,

где Σ P – сумма всех потерь в двигателе, Вт.

Ток холостого хода двигателя

.

При определении активной составляющей тока холостого хода принимают, что потери на трение и вентиляцию и потери в стали при холостом ходе двигателя такие же, как и при номинальном ре­жиме. При этом условии [1]

,

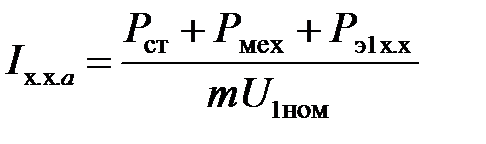где , причем .

 

Коэффициент мощности при холостом ходе:

cos φ _х.х = I _{х.х .а} / I _х.х .

 

1.4.8. Расчёт рабочих характеристик

Рабочими характеристиками асинхронных двигателей называют зависимости P ₁, I ₁, cosφ, η, s ₁ = f (P ₂). Часто к ним относят также за­висимости М = f (P ₂) и .

Определение коэффициента приведения с ₁ к Г-образной схеме замещения асинхронного двигателя:

с ₁ = x ₁ / x ₁₂,

где x ₁₂ = U _1н / I_𝜇 – x ₁.

Активная составляющая тока идеального холостого хода [1]:

,

Полное индуктивное сопротивление в схеме замещения:

X = с ₁(x ₁+ с₁ x' ₂).

Принимаем и для этого скольжения рассчитываем один столбец табл. 1. Если ток I ₁ и мощность P ₂ не будут отличаться от номинальных на 5%, то рассчитываем остальные столбцы таблицы. Шаг скольжения определяется отношением s _н / n, где n – число колонок. Если ток I ₁ существенно отличается от I _1н, то производится пересчет номинального скольжения на коэффициент I _1н / I₁.

 

Табл. 1

Результаты расчета

№	Расчётная формула	Ед.	Скольжение
				s н=
		Ом
		Ом
		Ом
		А
		—
		А
		А2
		—
	где I0p =I𝜇	А
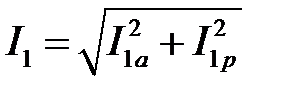
		А
		А
		Вт
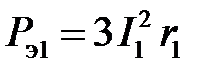
		Вт
		Вт
		Вт
		Вт
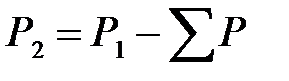
		Вт
		—
		—

 

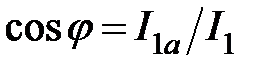
После окончания расчета для принятых значений скольжений строятся рабочие характеристики асинхронного двигателя (типовая форма приведена на рис. 4).

Рис. 4 – Рабочие характеристики асинхронного двигателя

 

1.4.9. Расчёт пусковых характеристик

Расчет начинается с режима короткого замыкания s = 1.

Определяется высота стержня паза ротора (рис. 2), м,

.

При литой алюминиевой обмотке ротора и ρ _с115 = 10^-6/20,5 Ом∙м определяется коэффициент ξ (читается – кси), от которого зависит вытеснение тока в роторе [1]:

.

По рис. П8Б и рис. П9Б определяются коэффициенты φ и k_Д = φ'.

Глубина проникновения в стержень, м,

h_r = h_r /(1+ φ).

1. Если глубина проникновения h_r находится в пределах (рис. 2) 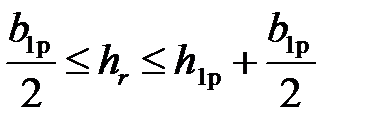, то площадь части сечения стержня, по которой протекает ток, определится по формуле:

,

где — ширина нижней части трапеции, ограниченной глубиной проникновения тока h_r.

2. Если 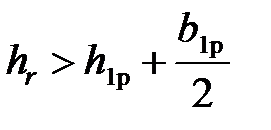принимают q_r ≈ q _c.

Коэффициент k_r определяют по отношению площадей всего се­чения стержня и сечения, ограниченного высотой h_r, т. е.

k_r = q_c /q_r,

где .

 

Так как в боковых замыкающих кольцах вытеснения тока нет, то общее увеличение активного сопротивления будет меньшим [1]:

.

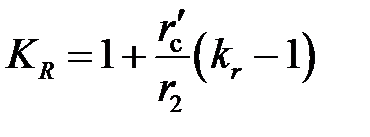Активное сопротивление фазы обмотки ротора с учетом вытес­нения тока равно:

.

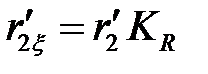Вытеснение тока в магнитной проводимости в пазовой части стержня учитывается коэффициентом демпфирования k _Д = φ ':

где k_I –кратность пускового тока k_I = 5…8. Процесс расчета можно начинать с k_I = 6,5 [1]. Кратность пускового тока k_I определится в конце расчета, когда будет найден ток в обмотке ротора с учетом вытеснения и насыщения :

.

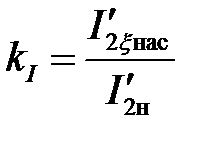Если конечное значение кратности пускового тока будет существенно отличаться от исходного (10 %), то необходимо произвести коррекцию в расчетах.

Обозначив коэффициентом К_X изменение индуктивного сопротивления фазы обмотки ротора от действия эффекта вытеснения тока, получим

,

где .

Ток ротора с учетом эффекта вытеснения :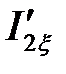

.

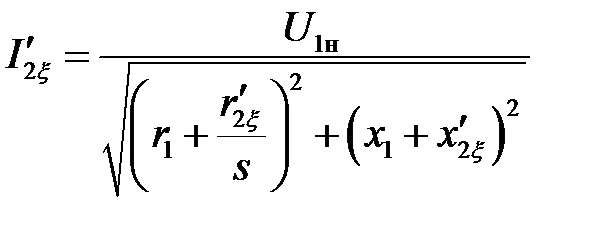Определяют среднюю магнитодвижущую силу (МДС) обмотки, отнесенную к одному пазу обмотки ста­тора [1]:

,

где . В этой формуле коэффициент укорочения шага обмотки ;

а – число параллельных ветвей обмотки статора;

u _п – число эффективных проводников в пазу статора;

– коэффициент, учитывающий уменьшение МДС паза, вызванное укорочением шага обмотки;

;

Коэффициент насыщения k _нас = 1,25…4. Процесс расчета можно начинать с k _нас = 1,35 [1]. Коэффициент насыщения k _насопределится в конце расчета, когда будет найден ток в обмотке ротора с учетом вытеснения и насыщения :

.

Если конечное значение коэффициента насыщения будет существенно отличаться от исходного (10%), то необходимо произвести коррекцию в расчетах.

По средней МДС F _п.cp рассчитывают фиктивную индукцию потока рассеяния в воздушном зазоре, Тл:

где (t ₁ и t ₂ – зубцовые деления статора и ротора).

По полученному значению B_ф𝛿 определяется отношение потока рассеяния при насыщении к потоку рассеяния ненасыщенной машины, характеризуемое коэффициентом ϰ_𝛿 (читается – каппа дельта) значение которого находят по рис. П10Б.

Далее рассчитывают значение дополнительного раскрытия паза статора [1]:

с _1рас = (t ₁ – b _ш1)·(1 – ϰ_𝛿).

Вызванное насыщением от полей рассеяния уменьшение коэф­фициента магнитной проводимости рассеяния полузакрытого паза статора:

.

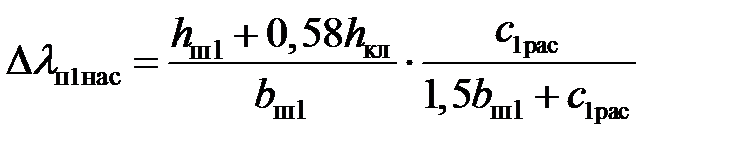Коэффициент магнитной проводимости пазового рассеяния при насыщении λ _п1нас определяют для статора по выражению

λ _п1нас = λ _п1 – Δ λ _п1нас,

где λ _п1 — проводимость, рассчитанная без учета насыщения.

Коэффициент проводимости дифференциального рассеяния при насыщении участков зубца статора λ _д1нас:

.

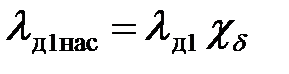Индуктивное сопротивление обмотки статора с учетом насыще­ния от полей рассеяния определяют по отношению сумм коэффици­ентов проводимости, рассчитанных без учета и с учетом насыщения от полей рассеяния:

,

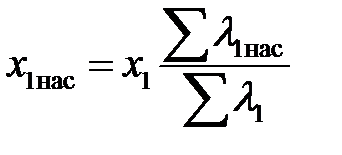где = .

Для короткозамкнутых роторов дополнительное рас­крытие рассчитывают по формуле:

с _2рас = (t ₂ – b _ш2)·(1 – ϰ_𝛿).

Уменьшение коэффициента проводимости для открытых и полу­закрытых пазов ротора [1]:

.

Коэффициент магнитной проводимости пазового рассеяния при насыщении λ _п2нас определяют для ротора по выражению

λ _п2нас = λ _{п2 ξ} – Δ λ _п2нас,

где λ _п2ξ – проводимость пазового рассеяния ротора для ненасыщен­ной зубцовой зоны с учетом влияния вытеснения тока.

Коэффициент проводимости дифференциального рассеяния при насыщении участков зубцов ротора λ _д2нас:

.

Индуктивное сопротивление обмотки ротора с учетом насыще­ния от полей рассеяния и действия эффекта вы­теснения тока определяют по отношению сумм коэффици­ентов проводимости, рассчитанных без учета и с учетом насыщения от полей рассеяния:

,

где = .

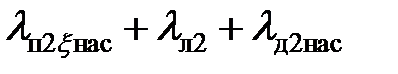Сопротивление взаимной индукции обмоток в пусковом режиме [1]:

.

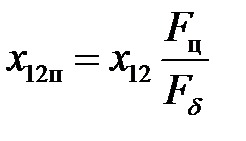Коэффициент c _1пнас определяется по формуле:

.

Расчет токов и моментов.

Активные и индуктивные сопротивления правой ветви Г- образной схемы замещения:

;

.

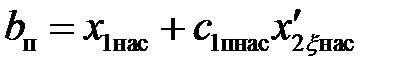Ток в обмотке ротора с учетом вытеснения насыщения:

.

Коэффициенты насыщения и кратности пускового тока:

; .

Ток в обмотке статора с учетом вытеснения насыщения [1]:

.

Сравнить с упрощенным выражением .

Относительное значение статорного пускового тока :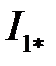

.

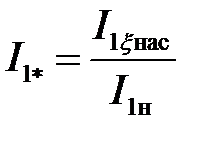Относительное значение пускового момента:

^.

Определение критического скольжения:

,

где и 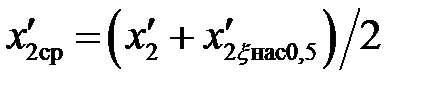, причем индуктивные сопротивления при насыщении (вытеснении) и будут известны только при расчете со следующим скольжением s = 0,5.

В пояснительной записке подробный расчет приводится только для скольжения s = 1, а для скольжений s = 0,5 и s = s _кр результаты расчетов приводятся в виде таблицы 2.

Зависимости М _∗ и I _1∗ от скольжения должны быть представлены на миллиметровой бумаге (типовая форма приведена на рис. 5).

Табл. 2

Результаты расчёта

№ п/п	Расчётная формула	Ед.	Скольжение
	0,5	s кр =
	ξ	—
	φ (ξ)	—
		—
		—
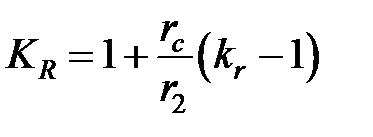
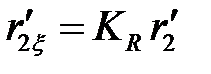
		Ом
		—
		—
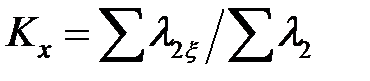
		Ом
		Ом
		Ом
		—
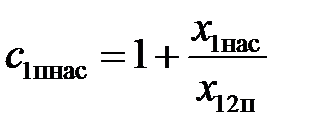
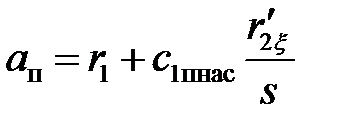
		Ом
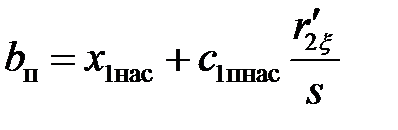
		Ом
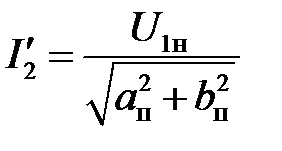
		А
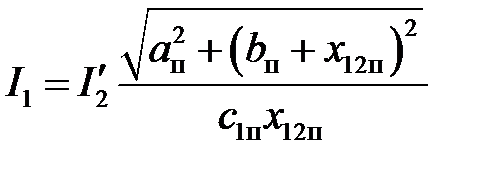
		А
		—
		—

 

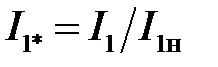
Рис. 5 – Зависимость тока и момента асинхронного двигателя от скольжения

1.4.10. Тепловой расчёт

1. Превышение температуры внутренней поверхности сердечника статора над температурой воздуха внутри машины, °С,

,

где α ₁ – коэффициент теплоотдачи с поверхности, определяемый по рис. П13Б;

К – коэффици­ент, учитывающий, что часть потерь в сердечнике статора и в пазовой части обмотки передается через станину непосредственно в окружаю­щую среду (по табл. П15А);

не должна превышать 25°С.

Электрические потери в обмотке статора в пазовой части, Вт,

,

где – электрические потери в статорной обмотке при s _н (по таблице 1); коэффици­ент k_ρ, в соответствии [1] принимается k_ρ =1,07.

2. Перепад температуры в изоляции пазовой части обмотки статора, °С,

,

где П _п1 ­­– расчетный периметр поперечного сечения паза статора, равный для полузакрытых трапецеидальных пазов, м: ;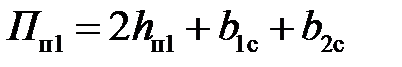

b _из – односторонняя толщина изоляции в пазу; для всыпной обмот­ки b _из берется по табл. П8А, м;

λ _экв — сред­няя эквивалентная теплопроводность пазовой изоляции; для класса нагревостойкости F: λ _экв = 0,16 Вт/(м°С);

λ' _экв — среднее значение коэффициента теплопроводности внутренней изоляции катушки всыпной обмотки из эмалированных проводников с учетом неплот­ности прилегания проводников друг к другу по рис. П11Б, Вт/(м°С). не должен превышать 5°С.

3. Перепад температуры по толщине изоляции лобовых частей

,

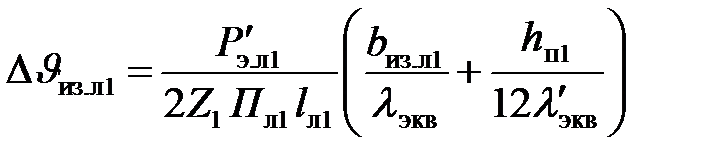где П _л1 – периметр условной поверхности охлаждения лобовой час­ти одной катушки; П _л1 ≈ П _п1;

b _из.л1 – односторонняя толщина изо­ляции лобовой части катушки. При отсутствии изоляции в лобовых частях b _из.л1 = 0;

λ' _экв для всыпной обмотки опре­деляется по рис. П11Б.

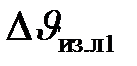не должен превышать 5°С.

Электрические потери в обмотке статора в лобовой части, Вт,