Глава 3. Метод средних арифметических

Суть метода

Идея метода в простейшем его осуществлении принадлежит Фробениусу, но связывают его обычно с именем Чезаро, который дал методу дальнейшее развитие.

По частичным суммам данного числового ряда (А) строятся их последовательные средние арифметические

Если варианта при имеет предел А, то это число и называют “обобщенной (в смысле Чезаро) суммой” данного ряда.

Примеры.1) Возвращаясь к ряду

Имеем здесь

так что 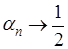. Мы пришли к той же сумме, что и по методу Пуассона-Абеля.

2) Для ряда . Частичные суммы будут (если только )

Теперь нетрудно подсчитать средние арифметические:

Итак, окончательно

Очевидно, : для значений “обобщенной суммой” и здесь служит 0.

3) Наконец, пусть снова предложен ряд

Имеем при ,

и затем

Отсюда ясно, что

Во всех случаях по методу Чезаро получилась та же “обобщенная сумма", что и выше, по методу Пуассона-Абеля. Оказывается это не случайность.

Взаимоотношение между методами Пуассона-Абеля и Чезаро

Начнем с простого замечания: если ряд (А) суммируем по методу средних арифметических к конечной “сумме” А, то необходимо

Действительно, из и следует, что

а тогда и

что и требовалось доказать.

Теорема (Фробениуса). Если ряд (А) суммируем по методу средних арифметических к конечной “сумме” А, то одновременно он суммируем также по методу Пуассона-Абеля и притом к той же сумме.

Доказательство. Итак, пусть . Ввиду сделанного вначале замечания очевидна сходимость степенного ряда

для 0<x<1. Выполнив дважды преобразование Абеля, последовательно получим

[при этом следует помнить, что ].

Известно, что (для 0<x<1) или

Умножим обе части тождества на А и вычтем из него почленно предыдущее тождество:

Сумму справа разобьем на две:

Причем число N выберем так, чтобы при было

где - произвольное наперед заданное положительное число. Тогда вторая сумма по абсолютной величине и сама будет меньше (независимо от ), а для первой суммы того же можно добиться за счет приближения x к 1. Этим и завершается доказательство.

Итак, мы установили, что во всех случаях, где приложим метод Чезаро, приложим и метод Пуассона-Абеля с тем же результатом.

Обратное же неверно: существуют ряды суммируемые методом Пуассона-Абеля, но не имеющие “обобщенной суммы" в смысле Чезаро. Рассмотрим, например, ряд

Так здесь явно не соблюдено необходимое условие суммируемости по методу средних арифметических, то этот метод не приложим. В то же время ряд

Имеет (при 0<x<1) сумму , которая при стремится к пределу . Это и есть “обобщенная сумма" нашего ряда по Пуассону-Абелю.

Таким образом, метод Пуассона-Абеля является более мощным, то есть приложим в более широком классе случаев, чем метод Чезаро, но не противоречит ему в тех случаях, когда они оказываются приложимыми оба.

Теорема Харди-Ландау

Как и в случае Пуассона-Абеля, для метода Чезаро также могут быть доказаны теоремы “тауберовского” типа, устанавливающие те дополнительные условия относительно членов ряда, при наличии которых из суммируемости ряда по методу средних арифметических вытекает его сходимость в обычном смысле слова. Ввиду теоремы Фробениуса ясно, что каждая тауберовская теорема для метода Пуассона-Абеля приводит, в частности, к такой же теореме для метода Чезаро. Например, сама теорема Таубера перефразируется теперь так: если и выполняется условие

( 9)

то одновременно и . Впрочем, здесь она непосредственно вытекает из легко проверяемого тождества

которое для данного случая указывает даже на необходимость условия (9).

Харди установил, что заключение от к можно сделать не только, если , но и при более широком предположении, что

().

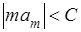Ландау показал, что можно удовольствоваться даже “односторонним” выполнением этого соотношения;

Теорема. Если ряд (А) суммируем к “сумме” А по методу средних арифметических и при этом выполняется условие (), то одновременно и

[Изменяя знаки всех членов ряда, видим, что достаточно также предположить неравенство другого смысла:

В частности, теорема, очевидно приложима к рядам с членами постоянного знака.

Доказательство. Для доказательства рассмотрим сначала сумму

где n и k - произвольные натуральные числа; путем тождественного преобразования она легко приводится к виду

(10)

Если взять любое (при ), то используя предположенное неравенство , можно получить такую оценку снизу:

откуда, суммируя по m, найдем

Отсюда, сопоставляя с (10), приходим к такому неравенству:

. (11)

Станем теперь произвольно увеличивать п до бесконечности, а изменение k подчиним требованию, чтобы отношение стремилось к наперед заданному числу . Тогда правая часть неравенства (11) будет стремиться к пределу , так что для достаточно больших значений п будет