Мы уже знакомы с методом средних арифметических; он является простейшим из бесконечной последовательности методов суммирования, предложенных Чезаро.
Фиксируя натуральное число к, Чезаро вводит варианту
и ее предел при 
рассматривает как “обобщенную сумму" (к -го порядка) ряда (А). При к =1 мы возвращаемся к методу средних арифметических.
В дальнейшем нам не раз понадобится следующее соотношение между коэффициентами:
Он легко доказывается по методу математической индукции относительно n, B и если исходить из известного соотношения
. (14)
Прежде всего, покажем, что методы Чезаро всех порядков являются частными случаями регулярных методов Вороного. Для этого достаточно положить 
, ибо из (14) тогда следует, что 
и к тому же, очевидно,
С помощью того же равенства (14), пользуясь самим определением величин 
, устанавливается, что
. (15)
Это дает возможность выяснить взаимоотношение между суммированием по Чезаро к -го и (к-1) - го порядка. Пусть ряд (А) допускает суммирование (к-1) - го порядка, так что 
. В силу (14) и (15) имеем
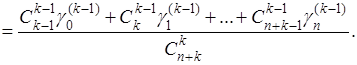
Применяя сюда теорему Теплица, причем полагаем
придем к заключению, что и 
. Таким образом, если ряд (А) допускает суммирование по методу Чезаро какого-нибудь порядка, то он допускает и суммирование любого высшего порядка, и притом к той же сумме.
Приведем теперь обобщение уже известной нам теоремы Фробениуса: если ряд (А) суммируем по какому-либо из методов Чезаро (скажем к -го порядка), то он суммируем к той же сумме и по методу Пуссона-Абеля.
Доказательство. Пусть дано, что
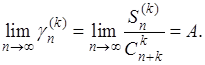(16)
Легко заключить отсюда, что ряд
(17)
для - 1<x<1 сходится. Действительно, так как 
то из (16) имеем:
Если 
, то
так что по теореме Коши-Адамара, радиус сходимости ряда (17) равен 1. Он во всяком случае не меньше 1, если А =0.
Рассмотрим теперь ряд тождеств
[2]
Выше мы установили сходимость последнего ряда в промежутке (-1,1); отсюда вытекает сходимость и всех предшествующих рядов. Кроме того,
(18)
Сопоставим с этим тождеством другое:
(19)
которое имеет место в том же промежутке (-1;
1); оно получается к -кратным дифференцированием прогрессии
Умножив обе части тождества (19) на А и вычитая из него почленно равенство (18), получим наконец,
Дальнейшие рассуждения [с учетом (16)] вполне аналогичны тем, с помощью которых была доказана теорема Абеля и теорема Фробениуса. В результате мы и получим:
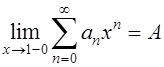
что и требовалось доказать.
Отметим, что существуют расходящиеся ряды, суммируемые по методу Пуассона-Абеля, но не суммируемые ни одним из обобщенных методов Чезаро. Таким образом, первый из названных методов оказывается сильнее всех последних, даже вместе взятых.
Метод Бореля
Он состоит в следующем: по ряду (А) и его частичным суммам 
строится выражение:
Если последний ряд сходится, хотя бы для достаточно больших значений х, и его сумма при 
имеет предел А, то это число и является “обобщенной суммой” в смысле Борелядля данного ряда (А).
Докажем регулярность метода Бореля. Допустим сходимость ряда (А) и обозначим его сумму через А, а остатки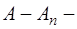 
через 
. Имеем (для достаточно больших х)
Зададимся произвольно малым числом 
; найдется такой номер N, что для 
будет:
.
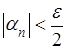Представим последнее выражение в виде суммы,
.
Второе слагаемое по абсолютной величине 
, каково бы ни было х, а первое представляющее собой произведение 
на многочлен, целый относительно х, становится абсолютно при достаточно больших х. Этим все доказано.
Метод Эйлера
Пусть дан ряд 
. Формула, выражающая “преобразование Эйлера” выглядит следующим образом
. (20)
При этом, как было доказано, из сходимости ряда в левой части вытекает сходимость ряда в правой части и равенство между их суммами.
Однако и при расходимости первого ряда второй ряд может оказаться сходящимся; в подомном случае его сумму Эйлер приписывал в качестве “обобщенной суммы" первому ряду. В этом собственно и состоит метод Эйлера суммирования рядов; сделанное только что замечание гарантирует регулярность метода.
Если писать рассматриваемый ряд в обычном виде (А), не выделяя знаков 
, и иметь в виду вырыжение
для р- ой разности, то можно сказать, что методу суммирования Эйлера в качестве “обобщенной суммы" ряда (А) берется обычная сумма ряда
(в предположении, что последний сходится)
Методы Гельдера представляют собой ещё один класс методов обобщенного суммирования. Но они состоят в простом повторении метода средних арифметических. Поэтому рассматривать их не стоит.
Заключение
В своей дипломной работе я рассмотрел методы суммирования расходящихся рядов, теоремы, вытекающие из этих методов, а также взаимосвязь этих методов между собой. Мы увидели многообразие подходов к вопросу суммирования расходящихся рядов. Регулярность каждого метода мы устанавливали во всех случаях. К сожалению, я не всегда имел возможность достаточно углубиться в вопрос о взаимоотношении этих методов между собой. А между тем может случиться, что два метода имеют пересекающиеся области приложимости, или, наоборот, может оказаться и что два метода приписывают одному и тому же расходящемуся ряду различные “обобщенные суммы”.
Теория рядов является важным и широко используемым разделом математического анализа, или другими словами бесконечные ряды являются важнейшим орудием исследования в математическом анализе и его приложениях.
Список использованной литературы
1. Выгодский М.Я. Справочник по высшей математике. М., 1982.
2. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах, часть 1, М., 1974.
3. Зельдович Я.Б. Высшая математика для начинающих. М., 1970.
4. Леонтьев А.Ф. Целые функции. Ряды экспонент. М., 1983.
5. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления, I, II т., М., 1966.
[1] Хотя формулировка метода “обобщенного суммирования ” принадлежит Пуассону, этот метод называют всё же методом Абеля, так как Пуассон применил этот метод лишь в частном случае. Поэтому в дальнейшем мы будем называть этот метод – методом Пассона-Абеля.
[2] Здесь и дальше учитываются соотношения типа (15)