Содержание
Предисловие……………………………………………………………….........................5
Основные обозначения…………………………………………………………………..6
Введение…………………………………………………………………………………..8
1 Комплексные числа. Алгебраические операции над комплексными числами…..10
1.1 Определение комплексного числа. Формы записи комплексных чисел…………10
1.2 Действия над комплексными числами……………………………..........................12
1.3 Возведение комплексного числа в целую степень и извлечение корня из комплексных чисел…….....……..…..………..………………………………………….15
1.4 Множества точек на комплексной плоскости. Задание геометрических мест…..17
1.5 Задачи для самостоятельного решения…………………………………………….20
2 Функции комплексного переменного……………………………………...................22
2.1 Основные геометрические понятия. Определение функции комплексного переменного. Геометрическая интерпретация функции комплексного переменного……………………………………………………………………..........22
2.2 Основные элементарные функции комплексного переменного……………………..25
2.3 Предел и непрерывность……………………………………………….................28
2.4 Задачи для самостоятельного решения…………………………………………….30
3 Аналитические функции. Условия Коши-Римана……………………………………32
3.1 Дифференцирование функции комплексного переменного. Аналитичность функции………………………………………………………..........................................32
3.2 Гармонические функции. Сопряженно-гармонические функции. Восстановление аналитической функции………………………………………...........33
3.3 Геометрический смысл модуля и аргумента производной………….....................34
3.4 Конформные отображения…………………………………………………………..34
3.5 Основная задача и общие теоремы теории конформных отображений………….35
3.6 Задачи для самостоятельного решения…………………………………………….38
4 Интегрирование функции комплексного переменного……………...……….39
4.1 Интеграл по кривой и его вычисление………………………………………………39
4.2 Теорема Коши. Интегральные формулы Коши……………………........................41
4.3 Задачи для самостоятельного решения…………………………………………….43
5 Ряды в комплексной области………………………………………….................45
5.1 Числовые ряды……………………………………………………………………….45
5.2 Степенные, сходящиеся к ним и двусторонние ряды…………………………............46
5.3 Ряды Тейлора и Лорана……………………………………………………………...48
5.3.1 Ряд Тейлора………………………………………………………...........................48
5.3.2 Ряд Лорана…...…………………………………………………………………….50
5.4 Задачи для самостоятельного решения…………………………………………….53
6 Нули функции. Изолированные особые точки……………………………….54
6.1 Нули аналитической функции…………………………………………………............54
6.2 Изолированные особые точки…………………………………………..........................54
6.3 Задачи для самостоятельного решения…………………………………………….56
7 Вычеты. Применение вычетов к вычислению интегралов…………….....................57
7.1Вычет функции и его вычисление……………………………………….................57
7.2 Основная теорема о вычетах и ее применение к вычислению контурных интегралов…………………………………………………………..................................58
7.3 Приложение вычетов к вычислению некоторых действительных интегралов…...59
7.4 Задачи для самостоятельного решения…………………………………………….61
8 Нахождение изображений…………………………………………………………….63
8.1 Определение оригинала и изображения……………………………………………63
8.2 Свойства преобразования Лапласа. Таблица основных изображений…………...64
8.3 Примеры вычислений изображений………………………………………………..67
8.4 Задачи для самостоятельного решения…………………………………………….69
9 Восстановление оригинала по изображению………………………………………...71
9.1 Элементарный метод………………………………………………………………...71
9.2 Теоремы разложения………………………………………………………………...72
9.3 Задачи для самостоятельного решения…………………………………………….75
10 Приложение операционного исчисления…………………………………………...76
10.1 Решение задач Коши для линейных дифференциальных уравнений с постоянными коэффициентами…………………………………………………………76
10.2 Задачи для самостоятельного решения…………………………………………...77
11 Варианты для самостоятельного решения………………………………….............78
12 Решение задач «нулевого варианта»………………………………………………...90
13 Из истории развития теории функций комплексного переменного……………..102
13.1 Первое появление комплексных чисел………………………………..................102
13.2 Возникновение теории функций комплексного переменного…………………104
13.3 Уточнение концепции комплексного числа…………………………………….107
13.4 Развитие комплексного интегрирования………………………….......................109
13.5 Из истории операционного исчисления………………………………………….112
14 Биографический словарь……………………………………………………………115
Список использованных источников...………………………………………………..129
Приложение А Некоторые оригиналы и их изображения…………………………...130
Основные обозначения

| – элемент 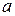 принадлежит множеству принадлежит множеству 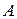
|

| – элемент 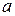 не принадлежит множеству не принадлежит множеству 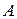
|

| – множество 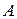 включено в множество включено в множество 
|

| – множество 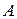 состоит из элементов состоит из элементов 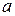 , ,  , , 
|

| – множество 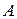 состоит из состоит из 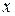 , обладающих свойством, указанным после двоеточия , обладающих свойством, указанным после двоеточия
|
| Ø | – пустое множество |
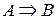
| – из высказывания 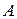 следует следует 
|

| – высказывания 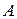 и и  равносильны равносильны
|
| N | – множество натуральных чисел |
| Z | – множество целых чисел |
| Q | – множество рациональных чисел |
| R | - множество действительных чисел |
| C | - множество комплексных чисел |

| - отрезок с концами в точках 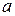 и и 
|
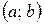
| - интервал с концами в точках 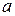 и и 
|
 , , 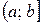
| - полуинтервалы с концами в точках 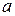 и и 
|

| - бесконечно удаленная точка расширенной комплексной плоскости |

| - сумма 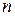 слагаемых, слагаемых, 
|
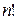
| - произведение всех натуральных чисел от 1 до 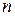 включительно включительно
|

| - точка  плоскости с координатами плоскости с координатами 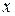 (абсцисса) и (абсцисса) и 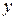 (ордината) (ордината)
|
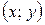
| - упорядоченная пара действительных чисел 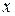 и и 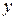
|

| - мнимая единица |

| - действительная и мнимая части комплексного числа |

| - число, сопряженное числу 
|

| - модуль комплексного числа 
|
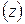
| - комплексная плоскость |

| - аргумент комплексного числа 
|

| - граница области 
|

| - замыкание области 
|

| - функция комплексного переменного 
|
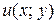 , , 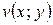
| - действительная и мнимая части функции  комплексного переменного комплексного переменного 
|

| - предел функции  при при 
|
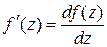
| - производная функции  комплексного переменного комплексного переменного 
|

| - частная производная функции 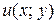 по переменной по переменной 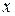
|

| - определенный интеграл от функции 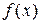 действительного переменного действительного переменного
|

| - интеграл от функции  комплексного переменного комплексного переменного  по ориентированной кривой по ориентированной кривой 
|

| - интеграл от функции  комплексного переменного комплексного переменного  по замкнутому контуру по замкнутому контуру 
|

| - вычет функции  комплексного переменного комплексного переменного  в точке в точке 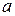
|
Ряды в комплексной области
Числовые ряды
Рассмотрим ряд с комплексными членами
 . (58)
. (58)
Теорема. Для сходимости ряда  необходимо и достаточно, чтобы сходились оба ряда:
необходимо и достаточно, чтобы сходились оба ряда:
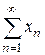 (
( )
)
 (
(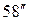 )
)
Определение. Ряд (58) называется абсолютно сходящимся, если сходится ряд
 (59)
(59)
Ряды ( ), (
), (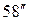 ) и (59) являются рядами с действительными членами, и вопрос об их сходимости решается с помощью известных признаков сходимости рядов в действительной области.
) и (59) являются рядами с действительными членами, и вопрос об их сходимости решается с помощью известных признаков сходимости рядов в действительной области.
Пример 1. Исследовать на сходимость ряд  .
.
а) имеем  . Таким образом, вопрос о сходимости данного ряда сводится к вопросу о сходимости рядов с действительными членами
. Таким образом, вопрос о сходимости данного ряда сводится к вопросу о сходимости рядов с действительными членами  и
и  . Так как каждый из рядов сходится абсолютно, то и данный ряд сходится абсолютно;
. Так как каждый из рядов сходится абсолютно, то и данный ряд сходится абсолютно;
б) приведем другое решение. Исследуем ряд на абсолютную сходимость, для чего составим ряд  – этот ряд сходится абсолютно.
– этот ряд сходится абсолютно.
Пример 2. Исследовать поведение ряда  .
.
Так как ряд  расходится, то расходится и исходный ряд.
расходится, то расходится и исходный ряд.