Метод основан на следующих общих соотношениях:
X i = j (X i –1, X i –2, …, X i – r) (mod M), (3.6)
x i = X i / M, (3.7)
где X i, — целые положительные числа (0 < X i < M);
X i –1, X i –2, …, X i – r — состояние датчика (r – количество чисел из предыстории, используемых для формирования следующего числа);
X0, X –1, X –2, …, X – r +1 – начальное состояние датчика;
- j(.)— функциональное преобразование состояния датчика в целое положительное число:
операция y = x (mod M), где M>1 – целое положительное число.
Это преобразование означает операцию вычисления остатка от целочисленного деления величины x на M ():
y = x – [ x /M]*M (здесь [.] – целая часть числа).
Очевидно, что (0 < y < M).
После нормирования (т.е. деления на М) получаем
x i – БПЧ (0 < x i < 1).
Различные варианты конгруэнтного метода моделирования различаются видом функции j(.).
Самый простейший – мультипликативный датчик:
X i = AX i –1(mod M), (3.8)
где A – целое положительное число, (А>1).
Структурная схема мультипликативного датчика представлена на рис.3.3.
Рис.3.3
Эта схема наглядно показывает, что датчик представляет собой дискретную динамическую автоколебательную систему с прямым запаздыванием (в отличие от разомкнутой системы физического датчика, питаемой извне нестандартным случайным процессом).
В такой системе при определенных условиях, которые зависят от параметров А, М, X0, будет реализовываться достаточно длительный переходный процесс неустойчивого характера.
Неустойчивость процесса по своим внешним проявлениям напоминает случайный характер протекания процесса и поэтому используется для имитации случайности.
С течением времени переходный процесс заканчивается и система входит в автоколебательный режим. Длительность переходного процесса плюс один период автоколебаний равняются отрезку апериодичности, который для мультипликативного датчика определяет число выдаваемых им неповторяющихся чисел.
Операция у=х (mod M) реализует механизм квантования, очень схожий с механизмом квантования в физическом датчике. Это можно увидеть, изобразив работу мультипликативного датчика на итеративной плоскости (рис.3.4).
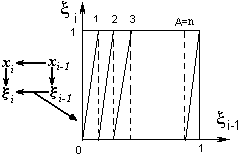
Рис.3.4
Зависимость x i от x i –1, как видно из рисунка, имеет пилообразный характер, аналогичный зависимости d(b) в физическом датчике. Она в данном случае реализует механизм квантования, обеспечивающий имитацию статистической равномерности.
Рассмотрим работу этого датчика при А=2 на итеративной плоскости при x0=1/3 (рис.3.5).
Рис.3.5
Видно, что в таком датчике сразу устанавливается автоколебательный режим с периодом в два числа: 1/3 и 2/3.
Предлагается самостоятельно проанализировать работу того же датчика с x0 = 5/12 (короткий переходный процесс с выходом на тот же самый автоколебательный режим), с x0 = 7/10 (достаточно длительный переходный процесс).
Выбор параметров мультипликативного датчика БПЧ
Чтобы датчик хорошо работал, к его параметрам X0, А и М предъявляются жесткие требования.
Соотношение этих параметров, во‑первых, определяет длину отрезка апериодичности.
О выборе величин М и Xо
Показано, что максимальная длина этого отрезка для мультипликативного датчика L= М – 1.
Для этого Xо и М должны быть взаимно простыми, а А – первообразным корнем уравнения 
=1(mod M) [ КорнГ., КонТ. Справочник по математике для научных работников и инженеров. М.: Наука, 1973г. ].
Таким образом, видно, что величина М должна быть достаточно большой, чтобы он мог выдавать большое число неповторяющихся чисел.
Кроме того, величина М влияет на быстродействие датчика. Составными частями операции у=х (mod M) являются деление и умножение на М. Если величину М брать равной М=2 b или M=10d (b и d – длины машинного слова в двоичном и, соответственно, десятичном компьютере), то операции умножения и деления на М в таких ЭВМ будут сводиться к сдвигу точки мантиссы числа.
Такое определение М, с одной стороны, обеспечит максимальное быстродействие датчика, а с другой стороны – максимальную длину отрезка апериодичности.
Но есть и отрицательный эффект такого выбора: младшие разряды БПЧ при этом оказываются достаточно сильно коррелированными [10]. Чтобы снизить коррелированность значение М для соответствующего компьютера выбирают равным 2 b –1 или 10d–1. Очевидно это приводит к снижению быстродействия датчика.