Тест заключается в проверке гипотезы о статистической равномерности распределения S‑мерных векторов, последовательно выбираемых из базовой последовательности: (x1, x2, …, xS), (xS+1, …,x2S), (x2S+1,…,x3S,),…, и т.д., — в S‑мерном единичном гиперкубе.
Один из тестов основывается на равномерном разбиении гиперкуба на части. Для этого отрезок [0,1] каждой оси гиперкуба разбивается на k частей. Тогда весь единичный гиперкуб разбивается на k S равных частей. По полученным реализациям S‑мерных базовых векторов строится многомерная гистограмма. Накопление статистики для ее построения может быть организовано с помощью одномерного массива m [ j ] (j =1,2,…,L) следующим образом.
Пусть получена некоторая реализация S‑мерного базового вектора (x1, x2, …,x j,…, xS).
Для каждой j ‑ой компоненты этого вектора определяется номер ячейки rj = [x j × k ]+1 (здесь [ b ] – целая часть числа b) по соответствующей оси единичного гиперкуба, в которую эта компонента попадает.
Тогда номер ячейки r одномерного массива m, в которой накапливается статистическая информация по данной реализации (m [ r ]:= m [ r ]+1), определяется следующим соотношением:
. (3.16)
Генерируется N векторов. По этим результатам рассчитываются частоты
P* r = m [ r ]/N. (3.17)
Соответствующие теоретические вероятности одинаковы и равны
P r = 1/ k S. (3.18)
Рассчитывается значение критерия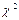 
:
. (3.19)
Проверка гипотезы о статистической равномерности последовательности БПЧ осуществляется с числом степеней свободы, равным (k S–1).
Параметрами проверки являются значения k, S, N. Относительно выбора их значений можно сказать следующее. На первый взгляд кажется, что чем большие значения k и S выбрать, тем точнее будет проверка. Но при этом необходимо учитывать следующее. Выбор N определяется значениями k и S. Для того, чтобы выводы, полученные с помощью критерия 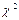, имели статистическую значимость, необходимо, чтобы в каждую ячейку многомерной гистограммы попало 20— 30 реализаций. Исходя из очевидных вероятностных соотношений NP r =N/ k S ³20¸30 видно, что необходимый объем выборки
N³ (20¸30) k S. (3.20)
Таким образом, видно, что выбор больших значений k и S приводит к значительной вычислительной сложности рассматриваемой тестовой проверки.
Кроме того, не в пользу необоснованного выбора больших значений k и S говорит также следующее. На большом объеме выборки N могут нивелироваться результаты плохой работы датчика на выборке меньшего объема. Тогда, проверив датчик на большом объеме выборки, а применяя в конкретной ИМ, требующей значительно меньшего числа БПЧ, можем получить большую методическую погрешность из‑за плохой работы датчика на этом малом объеме.
Окончательные рекомендации по выбору значений k, S, N таковы:
1) исходя из потребности ИМЭ на конкретной ИМ определяется объем выборки N для тестовой проверки,
2) затем подбираются значения k и S так, чтобы в каждую ячейку единичного гиперкуба попадало в среднем по 20 ¸ 30 реализаций S‑мерного вектора БПЧ.
Очевидные недостатки теста с равномерным разбиением единичного гиперкуба на части (большой требуемый объем выборки, и, следовательно, значительные затраты машинного времени, большая величина требуемой памяти ЭВМ) привели к созданию более эффективных тестов с неравномерным разбиением (так называемых, покер‑тестов). В них отдельные ячейки единичного гиперкуба после его равномерного разбиения объединяются по определенным признакам в непересекающиеся подобласти, полностью перекрывающие все пространство единичного гиперкуба. Теоретические вероятности попадания S‑мерного вектора БПЧ в эти подобласти рассчитываются с помощью формулы непосредственного подсчета вероятностей. Признаки объединения в подобласти, удовлетворяющие перечисленным свойствам, формулируются по соотношению номеров ячеек rj отдельных компонент реализаций S‑мерного вектора БПЧ.
Рассмотрим 5‑мерный покер‑тест (S=5). Вся информация по этому тесту при k =10 сведена в следующую таблицу 3.1.
Таблица 3.1
| № области | Области разбиения | Признаки формирования разбиения | теорет. вероятности |
| А0 | все пять rj разные | 0,3024 | |
| А1 | 1 пара rj одинаковых, остальные разные | 0,504 | |
| А2 | 2 пары rj одинаковых | 0,108 | |
| А3 | тройка rj одинаковых, остальные разные | 0,072 | |
| А4 | тройка rj одинаковых + пара rj одинаковых | 0,09 | |
| А5 | четверка rj одинаковых | 0,0045 | |
| А6 | все rj одинаковые | 0,0001 |
Как видно из этого примера, преимуществом покер‑теста является значительно меньшее число подобластей единичного гиперкуба, по которым накапливается статистика. Среди них только одна самая малая (А6) определяет объем выборки. При этом необходимо отметить следующее свойство образованных подобластей единичного гиперкуба, обеспечивающее во многом точность тестовой проверки статистической равномерности распределения БПЧ. Каждая область не сосредоточена в одном месте гиперкуба, а распределена по его объему (например, подобласть А0 объединяет ячейки равномерного распределения гиперкуба, расположенные по его диагонали).