Цель работы: Исследовать поведение интегральной функции принадлежности с точки зрения темпа ее сходимости к определенной ассимптоде в зависимости от методики ее вычисления и ее составляющих.
Краткие теоретические сведения:
Нечеткие множества – это частный случай нечисловых данных.
Пусть A - некоторое множество. Подмножество B множества A характеризуется своей характеристической функцией:
 (1)
(1)
Что такое нечеткое множество? Обычно говорят, что нечеткое подмножество C множества A характеризуется своей функцией принадлежности  . Значение функции принадлежности в точке х показывает степень принадлежности этой точки нечеткому множеству. Нечеткое множество описывает неопределенность, соответствующую точке х – она одновременно и входит, и не входит в нечеткое множество С. За вхождение -
. Значение функции принадлежности в точке х показывает степень принадлежности этой точки нечеткому множеству. Нечеткое множество описывает неопределенность, соответствующую точке х – она одновременно и входит, и не входит в нечеткое множество С. За вхождение -  шансов, за второе, т.е. за то, что точка не входит в множество, (1-
шансов, за второе, т.е. за то, что точка не входит в множество, (1-  ) шансов.
) шансов.
Если функция принадлежности  имеет вид (1) при некотором B, то C есть обычное (четкое) подмножество A. Таким образом, теория нечетких множество является более общей или хотя бы не менее общей математической дисциплиной, чем обычная теория множеств, поскольку обычные множества – частный случай нечетких. Соответственно можно ожидать, что теория нечеткости как целое обобщает классическую математику.
имеет вид (1) при некотором B, то C есть обычное (четкое) подмножество A. Таким образом, теория нечетких множество является более общей или хотя бы не менее общей математической дисциплиной, чем обычная теория множеств, поскольку обычные множества – частный случай нечетких. Соответственно можно ожидать, что теория нечеткости как целое обобщает классическую математику.
По степени общности обычная математика и нечеткая математика эквивалентны. Однако для практического применения, например, в теории принятия решений описание и анализ неопределенностей с помощью теории нечетких множеств весьма плодотворны.
Теория нечеткости является обобщением интервальной математики. Действительно, функция принадлежности:

задает интервальную неопределенность – про рассматриваемую величину известно лишь, что она лежит в заданном интервале [ a, b ]. Тем самым описание неопределенностей с помощью нечетких множеств является более общим, чем с помощью интервалов.
Л.А. Заде рассматривал теорию нечетких множеств как аппарат анализа и моделирования гуманистических систем, т.е. систем, в которых участвует человек. Его подход опирается на предпосылку о том, что элементами мышления человека являются не числа, а элементы некоторых нечетких множеств или классов объектов, для которых переход от «принадлежности» к «непринадлежности» не скачкообразен, а непрерывен. В настоящее время методы теории нечеткости используются почти во всех прикладных областях, в том числе при управлении предприятиями, качеством продукции и технологическими процессами, при описании предпочтений и оптимизации различных процессов, в том числе диагностического характера.
Л.А. Заде использовал термин «fuzzy set» (нечеткое множество). На русский язык термин «fuzzy» переводится как нечеткий, размытый, расплывчатый, и даже как пушистый и туманный.
В качестве примера аппарата теории нечетких множеств рассмотрим определения теоретико-множественных операций над нечеткими множествами. Пусть C и D - два нечетких подмножества A с функциями принадлежности  и
и  соответственно. Пересечением
соответственно. Пересечением  , произведением CD, объединением
, произведением CD, объединением  , отрицанием
, отрицанием  , суммой C+D называются нечеткие подмножества A с функциями принадлежности, соответственно:
, суммой C+D называются нечеткие подмножества A с функциями принадлежности, соответственно:

 .
.
Теория нечетких множеств в определенном смысле сводится к теории случайных множеств. Однако при решении прикладных задач вероятностно-статистические методы и методы теории нечеткости
Законы де Моргана для нечетких множеств. Законами же Моргана называются следующие тождества алгебры множеств:
 (2)
(2)
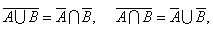 (3)
(3)
 (4)
(4)
Тождества (3) и (4) называются законами де Моргана для нечетких множеств.
Дистрибутивный закон для нечетких множеств. Некоторые свойства операций над множествами не выполнены для нечетких множеств. Так,  , за исключением случая, когда А – «четкое» множество (т.е. функция принадлежности принимает только значения 0 и 1).
, за исключением случая, когда А – «четкое» множество (т.е. функция принадлежности принимает только значения 0 и 1).
Носителем нечеткого множества А называется совокупность всех точек  , для которых
, для которых  .
.
Нечетким логическим выводом (fuzzy logic inference) называется
получение заключения в виде нечеткого множества, соответствующего текущим значениям входов, с использованием нечеткой базы знаний и нечетких операций.
В общем случае нечеткий вывод решения происходит за три (или четыре) шага:
1) этап фаззификации. С помощью функций принадлежности всех термов входных лингвистических переменных и на основании задаваемых четких значений из универсумов входных лингвистических переменных определяются степени уверенности в том, что выходная лингвистическая переменная принимает конкретное значение.
2) этап непосредственного нечеткого вывода. На основании набора правил - нечеткой базы знаний - вычисляются значения истинности для предпосылок всех правил на основании конкретных нечетких операций, соответствующих конъюнкции или дизъюнкции термов в левой части правил. В большинстве случаев это либо максимум, либо минимум из степеней уверенности термов, вычисленных на этапе фаззификации, который применяется к заключению каждого правила. Используя один из способов построения нечеткой импликации, получается нечеткая переменная, соответствующая вычисленному значению степени уверенности в левой части правила и нечеткому множеству в правой части правила.
Основным способом построения нечеткой импликации является способ Kleene-Dienes: пусть А и В - нечеткие высказывания и μAμB — соответствующие им функции принадлежности. Импликация А=>В определяется формулами:
А=>В ≡ Ā V В,
μА=>В (x, y) = max (1- μА (х); μВ (y)).
Однако, это не единственное обобщение оператора импликации. В таблице приведены другие интерпретации этого понятия, наиболее часто применяемые на практике.
| Larsen | μА=>В (x, y) = μА (х) μВ (y) |
| Lukasiewicz | μА=>В (x, y) = min (1; 1- μА (х) + μВ (y)) |
| Mamdani | μА=>В (x, y) = max (μА (х); μВ (y)) |
| Kleene-Dienes-Lu | μА=>В (x, y) = 1- μА (х)+ μА (х) μВ (y) |
3) этап композиции (агрегации, аккумуляции). Все нечеткие
множества, назначенные для каждого терма каждой выходной лингвистической лингвистической переменной, обьединяются вместе, и формируется единственное нечеткое множество - значение для каждой выводимой лингвистической переменной. Обычно используются функции MAX или SUM.
4) этап дефаззификации (необязательный). Используется тогда, когда полезно преобразовать нечеткий набор значений выводимых лингвистических переменных к точным. В теории нечетких множеств процедура дефузификации аналогична нахождению характеристик положения (математического ожидания, моды, медианы) случайных величин в теории вероятности. Имеется достаточно большое количество методов перехода к точным значениям.
Простейшим способом выполнения процедуры дефаззификации является выбор четкого числа, соответствующего максимуму функции принадлежности. Однако пригодность этого способа распространяется лишь на одноэкстремальные функции принадлежности. Для многоэкстремальных функций принадлежности часто используются следующие методы дефузификации:
1) COG (Center Of Gravity) – «центр тяжести»". Физическим аналогом этой формулы является нахождение центра тяжести плоской фигуры, ограниченной осями координат и графиком функции принадлежности нечеткого множества.
2) MOM (Mean Of Maximums) – «центр максимумов». При использовании метода центра максимумов требуется найти среднее арифметическое элементов универсального множества, имеющих максимальные степени принадлежностей.
3) First Maximum – «первый максимум» - максимум функции
принадлежности с наименьшей абсциссой.
Конкретные способы синтеза интегральных функций принадлежности определяется из характера решаемой задачи, ее целей и предметной области.
В связи с этим, на этапе разведочного анализа результатов мониторинга или в процессе диагностики целесообразно проводить исследование зависимости результирующей функции принадлежности от значений функции принадлежностей аргументов в нее входящих.
Порядок выполнения работы:
1. Изучить теоретические сведения - теорию нечетких множеств, принципы выбора и построения функций принадлежности, методы вычисления интегральной функции принадлежности.
2. На абстрактном носителе x синтезировать функции принадлежности согласно Таблице 1.
3. Согласно Таблице 2 составить алгоритм вычисления интегральной функции принадлежности в случае применения N решающих правил обладающих определенными функциями принадлежностями.
4. Оценить значения скорости и ускорения сходимости интегральной функции к единице в зависимости от количества решающих правил и выбранной функции принадлежности.
5. Проанализировать полученные результаты с точки зрения: сходимости, применения определенных функций принадлежности и методов вычисления интегральной функции, количества итераций в процессе вычисления.
6. Сделать выводы.
7. Оформить отчет, включающий в себя результирующую таблицу вида:
| Способ получения интегрального показателя | |
| Функция принадлежности | Скорость, ускорение, график |
8. В процессе самостоятельной работы в ходе выполнения лабораторной работы рекомендуется проанализировать показатели вычисления интегральной функции принадлежности в случаях изменения в итерациях как правил вычисления функций принадлежности, так и правил вычисления интегральной функции.
Таблица 1. – Типовые функции принадлежности
| Название функции | Вид функции |
| S | 
|
| π | 
|
| γ | 
|
| t | 
|
| L | 
|
Таблица 2 Интегральные функции принадлежности (пример)
| № | T(a,b) – «пересечение» | S(a,b) - «объединение» | параметры |
| Min(a,b) | Max(a,b) | ||
| a*b | a+b-a*b | ||
| MAX(a+b-1,0) | Min(a+b,1) | ||

| 
| ||

| 
| 
| |
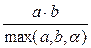
| 
| 
| |

| 
| p>0 | |

| 
| λ>0 | |

| 
| 
| |

| 
| w= min(1,1-a; 1,1-b) | |

| 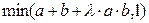
| 
|
Контрольные вопросы:
1. Чем отличается нечеткое множество от четкого?
2. Что такое функция принадлежности?
3. Как получить интегральное значение функции принадлежности в случае анализа нескольких нечетких множеств?
4. Что такое носптель функции принадлежности?
5. Когда рекомендуется применять аппарат теории нечетких множеств при построении диагностических правил?
6. В чем заключается алгоритмы нечеткого вывода Мамдани, Лоренса, Цукамото?
7. Что такое лингвистическая переменная?
8. Каким образом осуществляется коррекция интегральной функции принадлежности в случае неадекватно быстрого приближения ее значения к 1?
Практическая работа №2: