КОНТРОЛЬНАЯ РАБОТА
Задание 1
Вариант 1
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
345,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ673,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1001101.1101;
4. Произвести сложение с проверкой вычитанием:
а) 1100111,1101 + 11110011,1101=?
б) EF567,AD6 + 678ADE,567 =?
5. Произвести умножение двоичных чисел:
а) 11011,101* 1001,101 =?
Вариант 2
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
641,0025;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС873,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1101101.1001;
4. Произвести сложение с проверкой вычитанием:
а) 1010111,1011 + 11001111,10101=?
б) EF567,AВ + 678A4E,567 =?
5. Произвести умножение двоичных чисел:
а) 10011,101* 1101,101 =?
Вариант 3
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101;
4. Произвести сложение с проверкой вычитанием:
а) 1100101,1101 + 11010011,1101=?
б) 8F567,AD6 + 238ADE,567 =?
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
|
|
Вариант 4
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
567,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ233,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
110011.1101;
4. Произвести сложение с проверкой вычитанием:
а) 11010111,1101 + 11001011,1101=?
б) EFВ47,AD6 + 634ADE,577 =?
5. Произвести умножение двоичных чисел:
а) 101011,101* 1101,101 =?
Вариант 5
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
941,0025;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС8433,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1100001.1001;
4. Произвести сложение с проверкой вычитанием:
а) 1011111,1011 + 110010111,10101=?
б) EF597,AВ + 438A4E,567 =?
5. Произвести умножение двоичных чисел:
а) 11100,101* 1101,101 =?
Вариант 6
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101;
4. Произвести сложение с проверкой вычитанием:
а) 1100101,1101 + 11010011,1101=?
б) 8F567,AD6 + 238ADE,567 =?
|
|
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
Вариант 7
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
345,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ673,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1001101.1101;
4. Произвести сложение с проверкой вычитанием:
а) 1100111,1101 + 11110011,1101=?
б) EF567,AD6 + 678ADE,567 =?
5. Произвести умножение двоичных чисел:
а) 11011,101* 1001,101 =?
Вариант 8
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
641,0025;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС873,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1101101.1001;
4. Произвести сложение с проверкой вычитанием:
а) 1010111,1011 + 11001111,10101=?
б) EF567,AВ + 678A4E,567 =?
5. Произвести умножение двоичных чисел:
а) 10011,101* 1101,101 =?
Вариант 9
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101;
4. Произвести сложение с проверкой вычитанием:
|
|
а) 1100101,1101 + 11010011,1101=?
б) 8F567,AD6 + 238ADE,567 =?
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
Вариант 10
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
567,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ233,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
110011.1101;
4. Произвести сложение с проверкой вычитанием:
а) 11010111,1101 + 11001011,1101=?
б) EFВ47,AD6 + 634ADE,577 =?
5. Произвести умножение двоичных чисел:
а) 101011,101* 1101,101 =?
Вариант 11
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
941,0025;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС8433,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1100001.1001;
4. Произвести сложение с проверкой вычитанием:
а) 1011111,1011 + 110010111,10101=?
б) EF597,AВ + 438A4E,567 =?
5. Произвести умножение двоичных чисел:
а) 11100,101* 1101,101 =?
Вариант 12
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101;
4. Произвести сложение с проверкой вычитанием:
а) 1100101,1101 + 11010011,1101=?
б) 8F567,AD6 + 238ADE,567 =?
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
Вариант 13
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
345,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ673,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1001101.1101;
4. Произвести сложение с проверкой вычитанием:
а) 1100111,1101 + 11110011,1101=?
б) EF567,AD6 + 678ADE,567 =?
5. Произвести умножение двоичных чисел:
а) 11011,101* 1001,101 =?
Вариант 14
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
641,0025;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС873,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1101101.1001;
4. Произвести сложение с проверкой вычитанием:
а) 1010111,1011 + 11001111,10101=?
б) EF567,AВ + 678A4E,567 =?
5. Произвести умножение двоичных чисел:
а) 10011,101* 1101,101 =?
Вариант 15
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101;
4. Произвести сложение с проверкой вычитанием:
а) 1100101,1101 + 11010011,1101=?
б) 8F567,AD6 + 238ADE,567 =?
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
Вариант 16
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
567,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ233,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
110011.1101;
4. Произвести сложение с проверкой вычитанием:
а) 11010111,1101 + 11001011,1101=?
б) EFВ47,AD6 + 634ADE,577 =?
5. Произвести умножение двоичных чисел:
а) 101011,101* 1101,101 =?
Вариант 17
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
941,0025;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС8433,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1100001.1001;
4. Произвести сложение с проверкой вычитанием:
а) 1011111,1011 + 110010111,10101=?
б) EF597,AВ + 438A4E,567 =?
5. Произвести умножение двоичных чисел:
а) 11100,101* 1101,101 =?
Вариант 18
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101;
4. Произвести сложение с проверкой вычитанием:
а) 1100101,1101 + 11010011,1101=?
б) 8F567,AD6 + 238ADE,567 =?
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
Вариант 19
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
345,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ673,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1001101.1101;
4. Произвести сложение с проверкой вычитанием:
а) 1100111,1101 + 11110011,1101=?
б) EF567,AD6 + 678ADE,567 =?
5. Произвести умножение двоичных чисел:
а) 11011,101* 1001,101 =?
Вариант 20
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
641,0025;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС873,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1101101.1001;
4. Произвести сложение с проверкой вычитанием:
а) 1010111,1011 + 11001111,10101=?
б) EF567,AВ + 678A4E,567 =?
5. Произвести умножение двоичных чисел:
а) 10011,101* 1101,101 =?
Вариант21
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101;
4. Произвести сложение с проверкой вычитанием:
а) 1100101,1101 + 11010011,1101=?
б) 8F567,AD6 + 238ADE,567 =?
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
Вариант 22
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
567,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ233,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
110011.1101;
4. Произвести сложение с проверкой вычитанием:
а) 11010111,1101 + 11001011,1101=?
б) EFВ47,AD6 + 634ADE,577 =?
5. Произвести умножение двоичных чисел:
а) 101011,101* 1101,101 =?
Вариант 23
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
941,0025;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС8433,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1100001.1001;
4. Произвести сложение с проверкой вычитанием:
а) 1011111,1011 + 110010111,10101=?
б) EF597,AВ + 438A4E,567 =?
5. Произвести умножение двоичных чисел:
а) 11100,101* 1101,101 =?
Вариант 24
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101;
4. Произвести сложение с проверкой вычитанием:
а) 1100101,1101 + 11010011,1101=?
б) 8F567,AD6 + 238ADE,567 =?
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
Вариант 25
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
345,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ673,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1001101.1101;
4. Произвести сложение с проверкой вычитанием:
а) 1100111,1101 + 11110011,1101=?
б) EF567,AD6 + 678ADE,567 =?
5. Произвести умножение двоичных чисел:
а) 11011,101* 1001,101 =?
Вариант 26
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
641,0025;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС873,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1101101.1001;
4. Произвести сложение с проверкой вычитанием:
а) 1010111,1011 + 11001111,10101=?
б) EF567,AВ + 678A4E,567 =?
5. Произвести умножение двоичных чисел:
а) 10011,101* 1101,101 =?
Вариант 27
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101;
4. Произвести сложение с проверкой вычитанием:
а) 1100101,1101 + 11010011,1101=?
б) 8F567,AD6 + 238ADE,567 =?
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
Вариант 28
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
567,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ233,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
110011.1101;
4. Произвести сложение с проверкой вычитанием:
а) 11010111,1101 + 11001011,1101=?
б) EFВ47,AD6 + 634ADE,577 =?
5. Произвести умножение двоичных чисел:
а) 101011,101* 1101,101 =?
Вариант 29
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
941,0025;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС8433,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1100001.1001;
4. Произвести сложение с проверкой вычитанием:
а) 1011111,1011 + 110010111,10101=?
б) EF597,AВ + 438A4E,567 =?
5. Произвести умножение двоичных чисел:
а) 11100,101* 1101,101 =?
Вариант 30
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023;
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101;
4. Произвести сложение с проверкой вычитанием:
а) 1100101,1101 + 11010011,1101=?
б) 8F567,AD6 + 238ADE,567 =?
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
Задание 2
Вариант 1
1. Составить схему алгоритма и программу, вычисляющую заданный интеграл по формулам прямоугольников, трапеций или Симпсона. Найти наименьшее значение n, при котором каждая из формул дает приближенное значение интеграла с погрешностью, не превышающей eps. Вычислить погрешность по правилу Рунге.
,eps=0,0001.
2. Отделить корни уравнения x3-3x2+9x-8=0 графически и уточнить один из них методом Ньютона с точностью 0,001.
Вариант 2
1. Составить программу, вычисляющую заданный интеграл по формуле Гусса. Составить программу-функцию для вычисления значений подъинтегральной функции. Составить головную программу, содержащую обращение к вычислительным процедурам и осуществляющую печать результатов. Вычислить абсолютную и относительную погрешность.
, eps=0,0001
2. Отделить корни уравнения х - sinx = 0.25 графически и уточнить один из них методом простых итераций с точностью до 0,001
Вариант 3
1. Вычислить интеграл формулам прямоугольников, трапеций или Симпсона с двумя десятичными знаками. Для оценки погрешности использовать правило Рунге.
,eps=0,0001.
2. Методом наименьших квадратов найти квадратичную зависимость для экспериментальных данных, приведённых в таблице. В одной и той же системе координат изобразить график функции и точки.
| x | 4.5 | 5.0 | 5.5 | 6,0 | 6.5 |
| y | 7.7 | 9.4 | 11.4 | 13.6 | 15.6 |
Вариант 4
1. Решить систему нелинейных алгебраических уравнений методами Зейделя или простой итерации, точность данных методов e= 0,001
2. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
Вариант 5
1. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
2. Составить таблицу заданных конечных сумм. Размер сумм определены либо количеством членов N, либо требуемой точностью вычислений 
. В последнем случае добавление новых членов следует прекратить, если 
. Необходимо проделать анализ полученной таблицы, выявить наибольшее отклонение в таблице от точного значения и составить рекомендации по использованию конечных сумм.
Вариант 6
1. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
2. Вычислить интеграл формулам прямоугольников, трапеций или Симпсона с двумя десятичными знаками. Для оценки погрешности использовать правило Рунге.
,eps=0,0001.
Вариант 7
1. Найти действительный корень уравнения, лежащего в интервале [0.1;0.125] с точностью 10-4:
2. Решить систему линейных уравнений с точностью 
,
Вариант 8
1. Отделить корни уравнения 2x4+3x3+5x2-18=0 графически и уточнить один из них методом Ньютона с точностью 0,001.
2. Составить программу, вычисляющую заданный интеграл по формуле Гусса. Составить программу-функцию для вычисления значений подъинтегральной функции. Составить головную программу, содержащую обращение к вычислительным процедурам и осуществляющую печать результатов. Вычислить абсолютную и относительную погрешность.
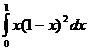
Вариант 9
1.
Вычислить абсолютную и относительную погрешность.
2. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
Вариант 10
1.
Вычислить абсолютную и относительную погрешность.
2. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
Вариант 11
1. Вычислить интеграл формулам прямоугольников, трапеций или Симпсона с двумя десятичными знаками. Для оценки погрешности использовать правило Рунге.
,eps=0,0001.
2. Методом наименьших квадратов найти квадратичную зависимость для экспериментальных данных, приведённых в таблице. В одной и той же системе координат изобразить график функции и точки.
| x | 4.5 | 5.0 | 5.5 | 6,0 | 6.5 |
| y | 7.7 | 9.4 | 11.4 | 13.6 | 15.6 |
Вариант 12
1. Для уравнения x2+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
2. Вычислить интеграл формулам прямоугольников, трапеций или Симпсона с двумя десятичными знаками. Для оценки погрешности использовать правило Рунге.
,eps=0,0001.
Вариант 13
1. Составить таблицу заданных конечных сумм. Размер сумм определены либо количеством членов N, либо требуемой точностью вычислений . В последнем случае добавление новых членов следует прекратить, если . Необходимо проделать анализ полученной таблицы, выявить наибольшее отклонение в таблице от точного значения и составить рекомендации по использованию конечных сумм.
2. Вычислить интеграл формулам прямоугольников, трапеций или Симпсона с двумя десятичными знаками. Для оценки погрешности использовать правило Рунге.
,eps=0,0001.
Вариант 14
1. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
2. Вычислить интеграл формулам прямоугольников, трапеций или Симпсона с двумя десятичными знаками. Для оценки погрешности использовать правило Рунге.
,eps=0,0001.
Вариант 15
1. Составить схему алгоритма и программу, вычисляющую заданный интеграл по формулам прямоугольников, трапеций или Симпсона. Найти наименьшее значение n, при котором каждая из формул дает приближенное значение интеграла с погрешностью, не превышающей eps. Вычислить погрешность по правилу Рунге.
,eps=0,0001.
2. Отделить корни уравнения x3-3x2+9x-8=0 графически и уточнить один из них методом Ньютона с точностью 0,001.
Вариант 16
1. Составить программу, вычисляющую заданный интеграл по формуле Гусса. Составить программу-функцию для вычисления значений подъинтегральной функции. Составить головную программу, содержащую обращение к вычислительным процедурам и осуществляющую печать результатов. Вычислить абсолютную и относительную погрешность.
, eps=0,0001
2. Отделить корни уравнения х - sinx = 0.25 графически и уточнить один из них методом простых итераций с точностью до 0,001
Вариант 17
1. Найти действительный корень уравнения, лежащего в интервале [0.1;0.125] с точностью 10-4:
2. Вычислить интеграл формулам прямоугольников, трапеций или Симпсона с двумя десятичными знаками. Для оценки погрешности использовать правило Рунге.
,eps=0,0001.
Вариант 18
1. Отделить корни уравнения 2x4+3x3+5x2-18=0 графически и уточнить один из них методом Ньютона с точностью 0,001.
2.Составить программу, вычисляющую заданный интеграл по формуле Гаусса. Составить программу-функцию для вычисления значений подъинтегральной функции. Составить головную программу, содержащую обращение к вычислительным процедурам и осуществляющую печать результатов. Вычислить абсолютную и относительную погрешность.
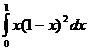
Вариант 19
1.
Вычислить абсолютную и относительную погрешность.
2. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
Вариант 20
1.
Вычислить абсолютную и относительную погрешность.
2. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
Вариант 21
1. Составить схему алгоритма и программу, вычисляющую заданный интеграл по формулам прямоугольников, трапеций или Симпсона. Найти наименьшее значение n, при котором каждая из формул дает приближенное значение интеграла с погрешностью, не превышающей eps. Вычислить погрешность по правилу Рунге.
,eps=0,0001.
2. Отделить корни уравнения x3-3x2+9x-8=0 графически и уточнить один из них методом Ньютона с точностью 0,001.
Вариант 22
1. Составить программу, вычисляющую заданный интеграл по формуле Гусса. Составить программу-функцию для вычисления значений подъинтегральной функции. Составить головную программу, содержащую обращение к вычислительным процедурам и осуществляющую печать результатов. Вычислить абсолютную и относительную погрешность.
, eps=0,0001
2. Отделить корни уравнения х - sinx = 0.25 графически и уточнить один из них методом простых итераций с точностью до 0,001
Вариант 23
1. Вычислить интеграл формулам прямоугольников, трапеций или Симпсона с двумя десятичными знаками. Для оценки погрешности использовать правило Рунге.
,eps=0,0001.
2. Методом наименьших квадратов найти квадратичную зависимость для экспериментальных данных, приведённых в таблице. В одной и той же системе координат изобразить график функции и точки.
| x | 4.5 | 5.0 | 5.5 | 6,0 | 6.5 |
| y | 7.7 | 9.4 | 11.4 | 13.6 | 15.6 |
Вариант 24
1. Решить систему нелинейных алгебраических уравнений методами Зейделя или простой итерации, точность данных методов e= 0,001
2. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
Вариант 25
1. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
2. Составить таблицу заданных конечных сумм. Размер сумм определены либо количеством членов N, либо требуемой точностью вычислений . В последнем случае добавление новых членов следует прекратить, если . Необходимо проделать анализ полученной таблицы, выявить наибольшее отклонение в таблице от точного значения и составить рекомендации по использованию конечных сумм.
Вариант 26
1. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
2. Вычислить интеграл формулам прямоугольников, трапеций или Симпсона с двумя десятичными знаками. Для оценки погрешности использовать правило Рунге.
,eps=0,0001.
Вариант 27
1. Найти действительный корень уравнения, лежащего в интервале [0.1;0.125] с точностью 10-4:
2. Решить систему линейных уравнений с точностью
,
Вариант 28
1. Отделить корни уравнения 2x4+3x3+5x2-18=0 графически и уточнить один из них методом Ньютона с точностью 0,001.
2. Составить программу, вычисляющую заданный интеграл по формуле Гусса. Составить программу-функцию для вычисления значений подъинтегральной функции. Составить головную программу, содержащую обращение к вычислительным процедурам и осуществляющую печать результатов. Вычислить абсолютную и относительную погрешность.
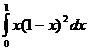
Вариант 29
1.
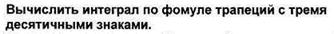
Вычислить абсолютную и относительную погрешность.
2. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
Вариант 30
1.
Вычислить абсолютную и относительную погрешность.
2. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ РАБОТЫ
Контрольная работа выполняется на диске, на которой помимо файлов, создаваемых согласно заданию, должен быть создан текстовый файл – этикетка с именем zadanie.doc, в который записывается: ФИО, группа, шифр зачетной книжки, № варианта задания, и список всех созданных в ходе выполнения задания файлов с необходимыми пояснениями.
Пример файла ZADANIE.DOC
| Фамилия, Имя, Отчество | Чапаев Василий Иванович | |
| Шифр зачетной книжки | 12456/97 | |
| Группа | ||
| Специальность | ||
| № контрольной работы | ||
| № варианта | ||
| Дата выполнения работы | 12.12.2003 | |
| Список файлов, созданных в ходе выполнения контрольной работы | ||
| zadan1.doc, | Отчёт к решению задачи | |
| Ref.doc | Файл Word с текстом реферата | |
| tab.xls | Таблица Excel c решением задачи | |
К диску должны быть приложены распечатки информации, находящейся на диске:
- файла-этикетки, оглавления диска и ее каталогов;
- текстовых файлов, электронных таблиц.
Контрольная работа должны быть выполнены и представлены на кафедру вычислительные системы и информационная безопасность не позднее первого декабря в ауд. 331. Проверенные работы студенты получают через месяц. При наличии замечаний преподавателя студенты обязаны внести дополнения и изменения в свои работы. К зачету и экзамену по дисциплине допускаются студенты, контрольные работы которых получили положительную оценку преподавателя.
Список рекомендуемой литературы
1. А.В. Басова, О.В. Смирнова и др. Краткий курс информатики, Ростов н/Д. ЮФУ, 2008г.
2. Ю.А.Стоцкий. Самоучитель. Office XP. — Питер, 2003г.
3. С.В. Симонович. Информатика. Базовый курс. — Питер, 2002г.
4. О.Э. Згадзай, С.Я. Казанцев, Л.А. Казанцева. Информатика для юристов. — Москва, 2001г.
5. Н. Угринович. Информатика и информационные технологии — М., БИНОМ, 2003г.
6. Н.В.Макарова. Информатика. — М., «Финансы и статистика», 2004г
7. Информатика. Практикум по технологии работы на компьютере. Под ред. Н.В.Макаровой. — М., «Финансы и статистика», 2004г.
8. Информатика. Серия «Учебники, учебные пособия».// Под ред. П.П.Беленького. – Ростов н/Д: Феникс, 2003.
9. Ляхович В.Ф. Основы информатики. - Ростов н/Д: Феникс, 2000.
10. Немнюгин С.А. Turbo Pascal. СПб: Питер, 2000.
11. Информатика. Базовый курс/ Под ред. С.В. Симонович – СПб: Издательство «Питер», 2000. –
640 с.
12. Информатика: Учебник. /Под ред. Н.В. Макаровой. – М: Финансы и статистика, 2001. – 768 с.
13. Фигурнов В.Э. IBM РС для пользователя. — М.: Информ. — М., 2000 — 432 с.
14. Р. Хершель. TURBO PASCAL — М.: МП