I начало ТД. Теплоемкости.

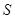Наиболее важными функциями состояния для характеристики системы являются внутренняя энергия , энтропия , энтальпия , свободная энергия .

Внутренняя энергия макросистемы складывается:

- из кинетической энергии поступательного и вращательного движения молекул системы,

- из потенциальной энергии колебательного движения атомов в молекулах;

- из потенциальной энергии взаимодействия между молекулами;

- из внутримолекулярной энергии (энергии электронных оболочек атомов и внутриядерной энергии).

, где суммирование идет по всем частицам системы.

Энергия поступательного движения системы как целого сюда не входит!

является внутренним параметром.

Возможны два способа изменения внутренней энергии системы:

I. Работа – способ передачи энергии, связанный с изменением внешних параметров. Договорились работу считать положительной, если система совершает работу, отрицательной 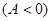, если работа совершается над системой.

II. Количество теплоты – способ передачи энергии без изменения внешних параметров. Договорились количество теплоты считать положительным , если теплота передается системе и отрицательной , если система отдает энергию.

Отметим, что количество теплоты, а так же работа не являются характеристиками системы, это величины, которые характеризуют обмен системы с внешней средой. Это способы передачи энергии, они определяются процессом.

I начало ТД обобщает закон сохранения энергии для ТД процессов: количество теплоты, сообщаемое системе, идет на изменение ее внутренней энергии и совершение системой работы.

- где знак 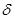- бесконечно малого приращения говорит о зависимости этого приращения от процесса.

Работа в случае отсутствия электрических и магнитных явлений сопровождается только расширением системы, которая находится под действием внешнего давления .

Элементарная работа газа при расширении .

В общем случае, работу при расширении можно найти, посчитав интеграл

Можно привести и другие формулировки I начала ТД:

Внутренняя энергия системы является однозначной функцией ее состояния и изменяется только под действием внешних воздействий.

, где 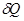- теплота, сообщенная системе;

- работа, совершенная над системой.

Следствие первого начала ТД: невозможен вечный двигатель первого рода, в котором работа, совершаемая системой больше количества теплоты, переданной системе,
т.к. если , то !!!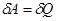

Изучаемые в ТД свойства систем могут быть разделены на два класса – термические и калорические. Те свойства, которые определяются только термическим уравнение состояния системы, называются ее термическими свойствами, те же свойства, которые определяются или только калорическим уравнением состояния, или совместно калорическим и термическим уравнением состояния, называются калорическими свойствами.

К калорическим свойствам относятся, прежде всего, теплоемкости и скрытые теплоты.

Скрытой теплотой изменения какого-либо внешнего параметра системы называется количество теплоты, необходимое для изменения этого параметра на единицу, при постоянной температуре и других внешних параметров.

Теплоемкость определяет количество теплоты, необходимое для изменения температуры системы на К, т.е. .

Поскольку количество теплоты 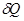, необходимое для изменения температуры системы на , зависит от характера происходящего при этом процесса, то и теплоемкость системы так же зависит от процесса. Это означает, что теплоемкость является не функцией состояния системы, а функцией процесса: одна и та же система в зависимости от происходящего в ней при нагревании процесса обладает различными теплоемкостями. Численно величина изменяется в пределах от до . Наибольшее практическое значение имеют теплоемкости и - теплоемкости для процессов при постоянном давлении и постоянном объеме. Теплоемкость величина аддитивная, поэтому в ТД чаще используются

удельная теплоемкость – теплоемкость единицы массы вещества: ,
и соответствующие ей удельные теплоемкости при постоянном давлении и объеме ,

молярная теплоемкость – теплоемкость одного моля вещества: ,
и соответствующие ей молярные теплоемкости при постоянном давлении и объеме .

С определение теплоемкости тесно связано понятие о термостате. Термостат – тело с настолько большой теплоемкостью 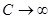, что его температура при теплообмене с какой-либо системой не меняется. Когда говорят о системе помещенной в термостат, то имеют в виду систему, в которой при всех происходящих в ней процессах (расширение, намагничивание и т.д.) температура поддерживается постоянной.

Первое начало ТД позволяет найти значения различных теплоемкостей и установить связь между ними, если известны термическое и калорическое уравнения состояния системы.

В общем случае внутренняя энергия является функцией объема и температуры (калорическое уравнение), тогда приращение внутренней энергии, выраженное через приращение независимых переменных .

Первое начало ТД для одного моля вещества с учетом калорического уравнения состояния

, отсюда

получим выражение для молярной теплоемкости:

В качестве иллюстрации рассмотрим ТД процессы над идеальным газом. Получим выражения для молярных теплоемкостей идеального газа.

Опыт показал (Гей-Люсак и Джоуль-Томсон, поставили опыт по расширению газа в пустоту), что внутренняя энергия идеального газа, который подчиняется уравнению состояния идеального газа, зависит только от температуры , и не зависит от занимаемого им объема.

Для идеального газа термическим уравнением состояния является уравнение Менделеева-Клапейрона для одного моля вещества .

В процессе при постоянном объеме , приращение , тогда I начало ТД

и .

Результаты опыта показывают, что у одноатомных газов теплоемкость не зависит от температуры. Для других идеальных газов существует слабая зависимость теплоемкости от температуры. Т.е. в широких температурных пределах можно считать для идеальных газов . Отсюда, учитывая, что для идеального газа внутренняя энергия является только функцией температуры , и не зависит от объема, получим для идеальных газов калорическое уравнение состояния:

В процессе при постоянном давлении над идеальным газом первое начало ТД с учетом выражения :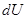

, тогда

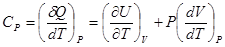
для одного моля идеального газа, учитывая уравнение состояния , и производные , , получим .

Таким образом, зная явный вид функции для идеального газа можно определить явный вид зависимостей значения молярных теплоемкостей.

Вспомним, что вывести сами уравнения состояния на основе начал ТД нельзя. Для каждой конкретной системы они определяются эмпирически, т.е. берутся из опыта, или находятся методами статистической физики. Так что в рамках ТД они считаются заданными при определении системы.

Для не слишком крайних условий явный вид функции для идеального газа может быть определен исходя из теоремы о равнораспределении энергии по степеням свободы. Доказательство теоремы мы рассмотрим в разделе статистической физики, а сейчас воспользуемся теоремой. Уточним, что степенями свободы называют независимые переменные. Число степеней свободы это число независимых переменных полностью задающих положение тела в пространстве.

Теорема: на каждую степень свободы молекул при поступательном и вращательном движении приходится энергии. На колебательную степень свободы - энергии.

Энергия колебательных движений системы очень велика, она обусловлена относительным смещением ядер, и тепловое движение при обычных температурах не может возбуждать колебательные степени свободы молекул системы. Тогда, т.к. энергия всех частиц системы, то внутренняя энергия для одного моля вещества идеального газа:

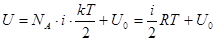, учли, что , т.к. постоянная Больцмана это универсальная газовая постоянная на одну молекулу. Дж/моль·К, Дж/К.

Тогда явный вид зависимостей для молярных теплоемкостей в процессах при постоянном объеме и давлении над идеальным газом:

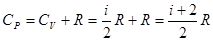Мы видим, что достаточно знать для данной системы сорт молекул и количество степеней свободы молекулы, чтобы вычислить значения молярных теплоемкостей и внутреннюю энергию моля вещества.

Вид молекул	число степеней свободы	на 1 моль вещества
Одноатомные	(поступательные ст.св.)
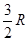
Двухатомные	(3 пост.+2 вращательные ст. св.)
Трехатомные и многоатомные	(3 пост.+3 вращательные ст. св.)