Условия равновесия и устойчивости систем.

Основное уравнение термодинамики для квазистатических процессов позволяет, как мы видели, ввести ряд термодинамических потенциалов, с помощью которых можно исследовать поведение термодинамических систем при этих процессах. Покажем теперь, что основное неравенство ТД для неравновесных процессов дает возможность с помощью введенных термодинамических потенциалов установить общие условия ТД равновесия и устойчивости различных систем. С точки зрения ТД эти условия являются достаточными, однако, допуская в соответствии с опытом существование флуктуаций в системах, можно доказать, что они являются также и необходимыми.

В применении к той или иной конкретной ТД системе общие условия равновесия и устойчивости позволяет получить частные (конкретные) для данной системы условия ее равновесия и устойчивости.

Теория термодинамического равновесия была развита Гиббсом по образцу механической статики Лагранжа, т.е. путем обобщения и распространения принципа виртуальных перемещений на ТД системы. Распространим этот способ определения условий равновесия на ТД системы. Состояние равновесия ТД системы определяется температурой и внешними параметрами , характеризующими отношение системы к внешним телам.

Согласно второму постулату ТД при равновесии все внутренние параметры являются функциями внешних параметров и температуры, и поэтому, когда и заданы, внутренние параметры не нужны для определения состояния равновесной системы. Если система отклонена от состояния равновесия, то внутренние параметры уже не являются функциями внешних параметров и температуры; поэтому неравновесное состояние необходимо характеризовать дополнительными независимыми параметрами. Это дает возможность рассматривать неравновесную систему как равновесную, но с большим числом параметров и соответствующих им обобщенных сил, «удерживающих» систему в равновесии, причем ТД функции системы в неравновесном состоянии будем считать равными значениям этих функций у равновесной системы с дополнительными «удерживающими» силами. (Роль таких сил играют внешние поля и адиабатические перегородки, отделяющие одну часть системы от другой, если температуры этих частей различны).

На основе такого представления, рассматривая выход системы из состояния равновесия как результат виртуальных отклонений внутренних параметров от их равновесных значений, можно, пользуясь основным неравенством ТД для необратимых процессов, получить общие для любых систем условия ТД равновесия и устойчивости. При этом, поскольку состояние ТД систем определяется не только механическими параметрами, но и специально ТД параметрами (температура, энтропия и др.), то, вместо одного общего условия равновесия для механических систем, для ТД систем их будет несколько, в зависимости от отношения системы к внешним телам (адиабатическая система, изотермическая система и др.).

Решая в каждом таком случае общее условие равновесия системы совместно с уравнениями для виртуальных изменений внутренних параметров, можно найти конкретные условия равновесия ТД систем.

1. Изолированная система: , , .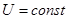

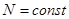Основное ТД неравенство для неравновесных процессов для такой системы при , , дает Þ 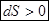, т.к. !

Т.е. энтропия изолированной системы при необратимых процессах возрастает. Когда эти процессы прекратятся, и наступит устойчивое равновесие, энтропия системы будет максимальна.

Таким образом, общим условием устойчивого равновесия изолированной системы является максимальность ее энтропии.

- необходимое условие, - достаточное условие.

Равенство нулю первой вариации является лишь необходимым условие экстремума и не обеспечивает того, чтобы энтропия имела именно максимум. Достаточным условием максимума энтропии является отрицательное значение ее второй вариации, которое обеспечивает устойчивость равновесия.

Если же при вторая вариация положительна (минимум энтропии), то соответствующее состояние системы будет равновесным, но совершенно неустойчивым (механический аналог – шар на вершине конуса), т.к. благодаря флуктуациям в ней начнутся неравновесные процессы, которые и приведут систему в равновесное состояние с максимумом энтропии. Т.к. дальше энтропия не может расти, то это состояние равновесия и будет устойчивым.

Равенство определяет общее условие равновесия, а неравенство - общее условие устойчивости равновесия изолированных ТД систем.

Т.о. наличие флуктуаций в системах приводит к необходимости максимума энтропии при равновесии и, следовательно, всякий раз, когда это условие не выполнено, система не находиться в устойчивом равновесии.

2. Система в термостате, при постоянном объеме: , , .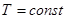

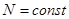Основное ТД неравенство для неравновесных процессов, приведенное к переменным 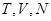, принимает вид , система в термостате не производит работы
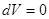, , дает .

В изотермической системе с постоянным объемом свободная энергия при необратимых процессах убывает и имеет минимум при устойчивом равновесии. Это общее условие равновесия устойчивости изотермической системы, не производящее внешней работы можно записать в виде 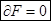- необходимое условие, - достаточное условие.

3. Система в термостате под постоянным внешним давлением: , ,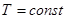

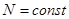
Основное ТД неравенство для неравновесных процессов, приведенное к переменным 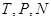, принимает вид , для системы, погруженной в среду с постоянной температурой и давлением, , , получаем .

Следовательно, в такой системе при неравновесных процессах энергия Гиббса убывает и имеет минимум при равновесии. Поэтому общее уравнение равновесия и устойчивости системы в термостате с постоянным внешним давлением – минимум энергии Гиббса, можно записать в виде - необходимое условие, - достаточное условие.

4. Система при постоянной энтропии и давлении: , , .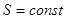

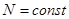Рассуждая аналогично, основное ТД неравенство, приведенное к переменным 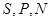, , для адиабатической системы, находящейся под постоянным внешним давлением , , , получаем .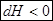

В такой системе при неравновесных процессах энтальпия убывает, и равновесие наступает при минимуме энтальпии.

Общее уравнение равновесия и устойчивости системы – минимум энтальпии, можно записать в виде - необходимое условие, - достаточное условие.

5. Система при постоянных энтропии и объеме: , , .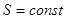

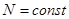Рассуждая аналогично, основное ТД неравенство, приведенное к переменным , , в изолированной адиабатической системе с постоянным объемом, , , 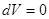, получаем .

В такой системе при неравновесных процессах внутренняя энергия убывает, и равновесие наступает при минимуме внутренней энергии.

Общее уравнение равновесия и устойчивости системы – минимум внутренней энергии, можно записать в виде - необходимое условие, - достаточное условие.

6. Система с переменным числом частиц в термостате при постоянных химических потенциалах и объеме: , , .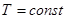

При изучении систем с переменным числом частиц чаще всего употребляют такой ТД потенциал, дифференцирование которого по соответствующим переменным позволяет найти числа частиц в системе каждого сорта.

Найдем этот потенциал, сделав преобразования Лежандра, перейдем в основном термодинамическом тожестве к дифференциальным переменным

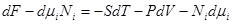Þ ,

, где

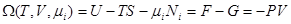- называют большим ТД потенциалом.

Тогда число частиц каждого сорта и другие характеристики системы находятся простым дифференцированием:

, ,

Для неравновесных процессов основное неравенство ТД для системы с переменным числом частиц при независимых переменных

система в термостате не производит работы
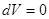, , дает .

В системе с переменным числом частиц, которая находится в термостате при постоянных , могут идти только процессы, при которых большой термодинамический потенциал убывает, и при устойчивом равновесии имеет минимум.

Общие условия равновесия и устойчивости такой системы, минимум большого ТД потенциала запишутся в виде - необходимое условие, - достаточное условие.

Т.о. общие условия устойчивого равновесия ТД систем в различных случаях определяются экстремальными значениями соответствующих ТД потенциалов.

ТД потенциалы могут иметь несколько экстремумов (например, энтропия имеет несколько максимумов). Состояния, соответствующие наибольшему или наименьшему из них, называются стабильными (абсолютно устойчивыми состояниями равновесия),
другие - метастабильными (полуустойчивыми). При наличии больших флуктуаций система может перейти из метастабильного состояния в стабильное состояние.